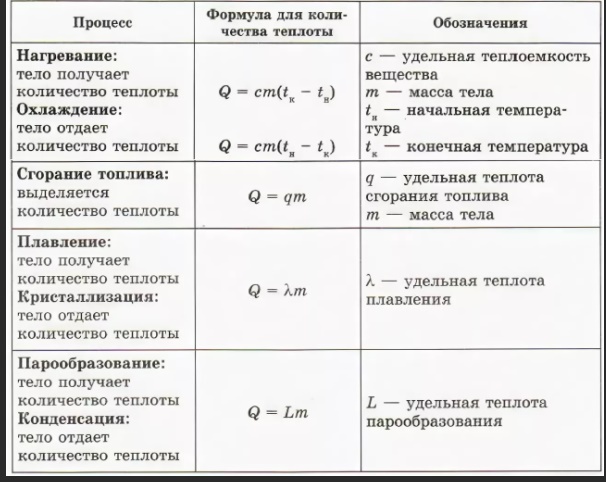
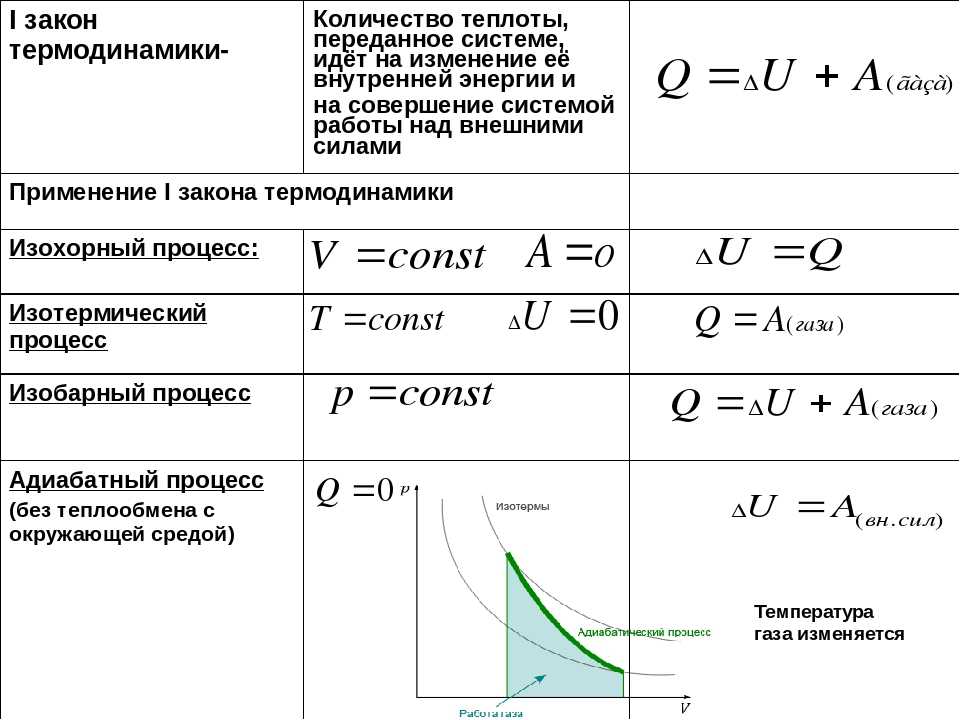
Формулы расчета платы за отопление в 2017 году
Статья актуальна на дату публикации на сайте. Расчеты размера платы действуют в 2019 году.
- Консультант ЖКХ
- Формулы расчета
Расчет платы за отопление в многоквартирном доме для жилых и нежилых помещений, коммунальных квартир, а также для жилых домов (домовладений) производится по формулам и методикам, указанным в Приложении № 2 к правилам, утвержденным Постановлением Правительства Российской Федерации от 06.05.2011 № 354.
Выбор методики расчета и формулы зависит от оборудования помещений и самих домов приборами учета на тепловую энергию (общедомовые (коллективные) приборы учета и индивидуальные приборы учета), периода оплаты за отопление, утвержденного в конкретном регионе, а также способа подачи тепловой энергии в дом (централизованная подача тепловой энергии или самостоятельное производство).
С 01 января 2019 года для расчета размера платы за отопление применяются следующие формулы:
Формулы для расчета платы за отопление для жилых и нежилых помещений, расположенных в многоквартирном доме:
Формула №2(3) применяется для расчета размера платы за отопление для жилого или нежилого помещения, расположенного в многоквартирном доме, не оборудованным общедомовым прибором учета тепловой энергии, при осуществлении оплаты за отопление в течение отопительного периода – Ознакомиться
Формула №2(5) применяется для расчета объема тепловой энергии для жилого или нежилого помещения, расположенного в многоквартирном доме, не оборудованным общедомовым прибором учета тепловой энергии, при осуществлении оплаты за отопление в течение отопительного периода – Ознакомиться
Формула №2(4) применяется для расчета размера платы за отопление для жилого или нежилого помещения, расположенного в многоквартирном доме, не оборудованным общедомовым прибором учета тепловой энергии, при осуществлении оплаты за отопление в течение календарного года (12 месяцев) – Ознакомиться
Формула №2(6) применяется для расчета объема тепловой энергии для жилого или нежилого помещения, расположенного в многоквартирном доме, не оборудованным общедомовым прибором учета тепловой энергии, при осуществлении оплаты за отопление в течение календарного года (12 месяцев) – Ознакомиться
Формула №3 применяется для расчета размера платы за отопление при наличии на многоквартирном доме общедомового прибора учета тепловой энергии, и в котором ни одно жилое или нежилое помещение не оборудовано индивидуальным прибором учета на отопление – Ознакомиться
Формула №3(6) применяется для расчета объема тепловой энергии в жилом или нежилом помещении при наличии на многоквартирном доме общедомового прибора учета тепловой энергии, и в котором ни одно жилое или нежилое помещение не оборудовано индивидуальным прибором учета на отопление – Ознакомиться
Формула №3(1) применяется для расчета размера платы за отопление при наличии на многоквартирном доме общедомового прибора учета тепловой энергии, и в котором хотя бы одно, но не все жилые или нежилые помещения, оборудованы индивидуальным прибором учета на отопление – Ознакомиться
Формула №3(7) применяется для расчета объема тепловой энергии в жилом или нежилом помещении при наличии на многоквартирном доме общедомового прибора учета тепловой энергии, и в котором хотя бы одно, но не все жилые или нежилые помещения, оборудованы индивидуальным прибором учета на отопление – Ознакомиться
Формула №3(3) применяется для расчета размера платы за отопление при наличии на многоквартирном доме общедомового прибора учета тепловой энергии, и в котором все жилые или нежилые помещения, оборудованы индивидуальным прибором учета на отопление – Ознакомиться
Формулы для расчета платы за отопление для жилого дома (домовладения):
Формула №2 применяется для расчета размера платы за отопление при отсутствии на жилом доме (домовладении) индивидуального прибора учета тепловой энергии, при осуществлении оплаты за отопление в течение отопительного периода – Ознакомиться
Формула №2(1) применяется для расчета размера платы за отопление при отсутствии на жилом доме (домовладении) индивидуального прибора учета тепловой энергии, при осуществлении оплаты за отопление равномерно в течение календарного года (12 месяцев) – Ознакомиться
Формула №3(5) применяется для расчета размера платы за отопление при наличии на жилом доме индивидуального прибора учета тепловой энергии – Ознакомиться
Формула №22 применяется для расчета размера платы за отопление в жилом доме (домовладении) при использовании им земельного участка и расположенных на нем надворных построек, если на жилом доме не установлен индивидуальный прибор учета на отопление.
Методика расчета тепловой энергии \ Акты, образцы, формы, договоры \ КонсультантПлюс
- Главная
- Правовые ресурсы
- Подборки материалов
- Методика расчета тепловой энергии
Подборка наиболее важных документов по запросу Методика расчета тепловой энергии (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).
- Теплоснабжение:
- Автономное отопление
- Актуализация схемы теплоснабжения
- Аренда котельной
- Бездоговорное потребление тепловой энергии
- Вентиляция
- Показать все
- Теплоснабжение:
- Автономное отопление
- Актуализация схемы теплоснабжения
- Аренда котельной
- Бездоговорное потребление тепловой энергии
- Вентиляция
- Показать все
Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня
Доказательства и доказывание в арбитражном суде: Теплоснабжение: ТСО хочет взыскать задолженность за поставленную по договору тепловую энергию
(КонсультантПлюс, 2023)Договором теплоснабжения (на отпуск тепловой энергии) с приложениями, допсоглашениями, в которых стороны согласовали все существенные условия, в частности порядок учета потребляемой тепловой энергии, договорный объем тепловой энергии, порядок расчетов и др. (п. 21 Правил организации теплоснабжения) >>>
(п. 21 Правил организации теплоснабжения) >>>
Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня
Подборка судебных решений за 2021 год: Статья 171 “Налоговые вычеты” главы 21 “Налог на добавленную стоимость” НК РФ
(Юридическая компания “TAXOLOGY”)Налогоплательщик выставил в адрес покупателей корректировочные счета-фактуры (с уменьшением объема поставки), поскольку судебными актами с покупателей (потребителей) была взыскана задолженность за поставленный ресурс в меньшем объеме, а также в связи с предоставлением налогоплательщику субсидии, направленной на возмещение понесенных экономических потерь (выпадающих доходов). Налоговый орган отказал налогоплательщику в принятии к вычету НДС на основании корректировочных счетов-фактур. Суд признал отказ правомерным, указав, что в соответствии с п. 2 ст. 154 НК РФ налоговая база по НДС определяется как стоимость реализованных товаров (работ, услуг), исчисленная исходя из фактических цен их реализации. Суммы субсидий при определении налоговой базы не учитываются. При получении налогоплательщиком субсидии изменение стоимости реализованных ресурсов, в том числе изменение тарифа на ресурсы и (или) уточнение количества (объема) реализованных ресурсов, у продавца не происходит. Таким образом, получение налогоплательщиком субсидии не является основанием для составления корректировочных счетов-фактур, поскольку при этом не происходит уменьшение налоговых обязательств, а происходит возмещение понесенных экономических потерь (выпадающих доходов). Также суд отметил, что размер подлежащей взысканию с потребителей задолженности был уменьшен судом не в связи с изменением объема поставленной тепловой энергии, а по причине изменения методики ее расчета, при этом в корректировочных счетах-фактурах налогоплательщик в одностороннем порядке изменил объем поставленной тепловой энергии, но при этом объем тепловой энергии, полученной от поставщика – производителя тепловой энергии, не корректировал. Суд указал, что само по себе наличие судебных актов о взыскании с покупателей (потребителей) задолженности за поставленную энергию для целей налогообложения не имеет значения, поскольку взыскание задолженности в меньшей сумме связано не с наличием оснований, предусмотренных п.
Суммы субсидий при определении налоговой базы не учитываются. При получении налогоплательщиком субсидии изменение стоимости реализованных ресурсов, в том числе изменение тарифа на ресурсы и (или) уточнение количества (объема) реализованных ресурсов, у продавца не происходит. Таким образом, получение налогоплательщиком субсидии не является основанием для составления корректировочных счетов-фактур, поскольку при этом не происходит уменьшение налоговых обязательств, а происходит возмещение понесенных экономических потерь (выпадающих доходов). Также суд отметил, что размер подлежащей взысканию с потребителей задолженности был уменьшен судом не в связи с изменением объема поставленной тепловой энергии, а по причине изменения методики ее расчета, при этом в корректировочных счетах-фактурах налогоплательщик в одностороннем порядке изменил объем поставленной тепловой энергии, но при этом объем тепловой энергии, полученной от поставщика – производителя тепловой энергии, не корректировал. Суд указал, что само по себе наличие судебных актов о взыскании с покупателей (потребителей) задолженности за поставленную энергию для целей налогообложения не имеет значения, поскольку взыскание задолженности в меньшей сумме связано не с наличием оснований, предусмотренных п. 13 ст. 171 НК РФ, а с применением различных методик.
13 ст. 171 НК РФ, а с применением различных методик.
Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня
“Справочник по доказыванию в арбитражном процессе”
(2-е издание, переработанное и дополненное)
(под ред. И.В. Решетниковой)
(“Норма”, “ИНФРА-М”, 2022)Так, в силу прямого указания п. 13 Правил N 354 условия договоров о приобретении коммунальных ресурсов в целях использования таких ресурсов для предоставления коммунальных услуг потребителям определяются с учетом названных Правил и иных нормативных правовых актов РФ. Приведенные законоположения в их системном истолковании в судебной практике рассматриваются как исключающие возложение на управляющую организацию – исполнителя коммунальных услуг в отношениях с ресурсоснабжающими организациями обязанностей по оплате коммунальных ресурсов в большем объеме, чем аналогичные коммунальные ресурсы подлежали бы оплате в случае получения гражданами – пользователями коммунальных услуг указанных ресурсов напрямую от ресурсоснабжающих организаций, минуя посредничество управляющей организации.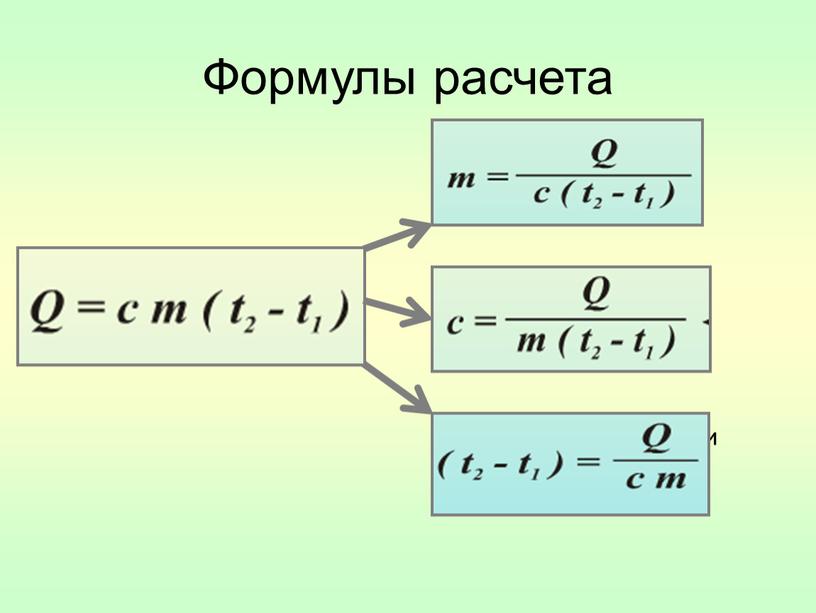 Из изложенного следует, что размер задолженности компании за коммунальный ресурс, поставленный в многоквартирном доме при отсутствии или неисправности общедомового прибора учета, необходимо рассчитывать по Правилам N 354; а расчет требований, основанный на Правилах коммерческого учета тепловой энергии, теплоносителя, утвержденных Постановлением Правительства РФ от 18 ноября 2013 г. N 1034, не соответствует закону .
Из изложенного следует, что размер задолженности компании за коммунальный ресурс, поставленный в многоквартирном доме при отсутствии или неисправности общедомового прибора учета, необходимо рассчитывать по Правилам N 354; а расчет требований, основанный на Правилах коммерческого учета тепловой энергии, теплоносителя, утвержденных Постановлением Правительства РФ от 18 ноября 2013 г. N 1034, не соответствует закону .
Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня
Статья: Расчет платы за отопление пропорционально объему отапливаемых помещений: такое возможно?
(Дубова Я.Г.)
(“Жилищно-коммунальное хозяйство: бухгалтерский учет и налогообложение”, 2021, N 1)В Верховный Суд обратилась одна из УК с административным исковым заявлением о признании недействующими п. п. 3, 3(1), 3(3), 3(6) приложения 2 к Правилам предоставления коммунальных услуг . Оспариваемые положения нормативного правового акта противоречат ч. 3 ст. 30, ч. 1 ст. 157 ЖК РФ, ст. 210 ГК РФ, вызывают неоднозначное толкование, нарушают права, свободы и законные интересы административного истца и граждан – собственников помещений в МКД, лишенных в отсутствие индивидуальных приборов учета справедливого распределения платы за отопление. О чем речь? Если на первых этажах жилых МКД находятся магазины с высотой потолков, превышающей высоту потолков квартир, то жители при отсутствии индивидуальных приборов учета оплачивают отопление магазинов. В такой ситуации – когда помещения, имеющие одинаковую площадь, значительно различаются между собой по высоте потолков – оплата отопления должна производиться не пропорционально площади, а пропорционально объему отапливаемых помещений. Тем самым УК предложила применить при расчете п. п. 115, 116 Правил коммерческого учета тепловой энергии, теплоносителя . Счел ли суд доводы УК справедливыми?
1 ст. 157 ЖК РФ, ст. 210 ГК РФ, вызывают неоднозначное толкование, нарушают права, свободы и законные интересы административного истца и граждан – собственников помещений в МКД, лишенных в отсутствие индивидуальных приборов учета справедливого распределения платы за отопление. О чем речь? Если на первых этажах жилых МКД находятся магазины с высотой потолков, превышающей высоту потолков квартир, то жители при отсутствии индивидуальных приборов учета оплачивают отопление магазинов. В такой ситуации – когда помещения, имеющие одинаковую площадь, значительно различаются между собой по высоте потолков – оплата отопления должна производиться не пропорционально площади, а пропорционально объему отапливаемых помещений. Тем самым УК предложила применить при расчете п. п. 115, 116 Правил коммерческого учета тепловой энергии, теплоносителя . Счел ли суд доводы УК справедливыми?
Формула теплоты реакции – GeeksforGeeks
Теплота реакции , также известная как Энтальпия реакции , представляет собой разницу в значении энтальпии химической реакции при постоянном давлении. Это термодинамическая единица измерения, используемая для определения общего количества энергии, произведенной или высвобожденной на моль в реакции. В результате теплота химической реакции может быть определена как теплота, выделяемая в окружающую среду или поглощаемая при протекании реакции при постоянном давлении и температуре. Джоуль (Дж) – это единица, используемая для измерения общего количества полученного или выделенного тепла.
Это термодинамическая единица измерения, используемая для определения общего количества энергии, произведенной или высвобожденной на моль в реакции. В результате теплота химической реакции может быть определена как теплота, выделяемая в окружающую среду или поглощаемая при протекании реакции при постоянном давлении и температуре. Джоуль (Дж) – это единица, используемая для измерения общего количества полученного или выделенного тепла.
В химических реакциях тепло в основном передается между реагирующей системой как одной средой и окружающей средой как другой. До и после химического превращения количество тепловой энергии одинаково. Другими словами, теплота, полученная или потерянная в реагирующей системе, эквивалентна теплоте, полученной или потерянной в окружающей среде.
Проще говоря, теплота реакции – это количество энергии, необходимое для проведения указанной реакции; он отрицателен для экзотермических реакций и положителен для эндотермических реакций. Здесь для эндотермической реакции ∆H положителен, тогда как ∆H отрицателен для тех реакций, которые выделяют тепло.
Здесь для эндотермической реакции ∆H положителен, тогда как ∆H отрицателен для тех реакций, которые выделяют тепло.
Когда данная реакция проводится при постоянном объеме, тепло, необходимое для воздействия на реакцию, представляет собой не что иное, как увеличение внутренней энергии (∆U) за счет ∆H/∆U, которое будет отрицательным для эндотермической реакции и положительным для экзотермической реакции .
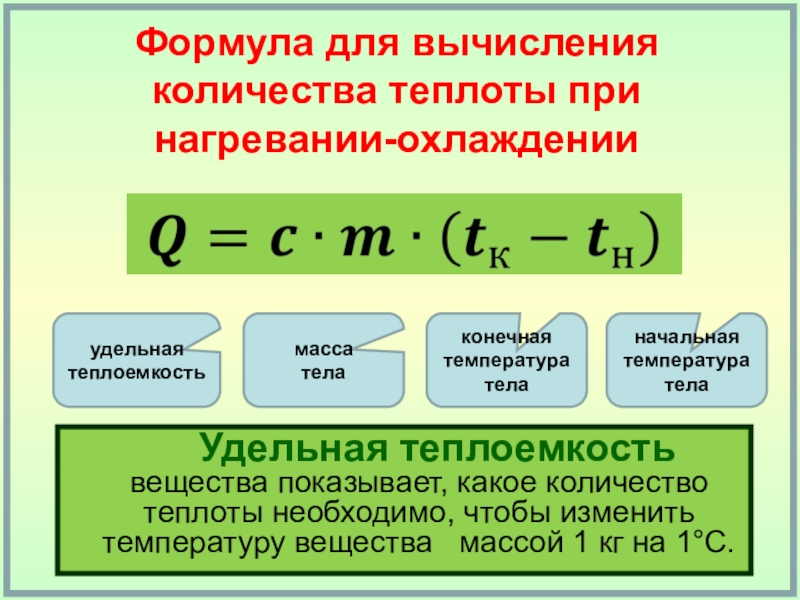
Формула теплоты реакцииQ = m × c × ΔT
Где,
- Q = теплота реакции,
- m = масса среды,
- c = удельная теплоемкость реакционная среда,
- ∆T = разница температур среды.
Кроме того, у нас есть еще одно уравнение:
Теплота реакции = ΔH (продукты) – ΔH (реагенты)
Где
- ΔH = изменение теплоты сгорания
Решенные примеры по теплу Формула реакции
Пример 1: Рассчитайте теплоотдачу, которая происходит при сгорании этанола при сжигании определенного количества вещества в воздухе для повышения температуры с 28 до 42 градусов Цельсия 200 г воды, при условии, что вода имеет удельную теплоемкость 4,2 Дж/г. К.
К.
Решение:
Дано, что
c = 4,2 Джг -1 K -1 ,
m = 200 г,
ΔT = 42 – 28 ,
т. е. ΔT = 14 °C или 14 K
Здесь в вопросе упоминается, что определенное количество этанола сжигается для повышения температуры воды, подразумевая, что тепло, поглощаемое водой, выделяется в процессе сгорания этанола. Количество теплоты, потерянное в процессе горения, равно количеству теплоты, полученному водой.
Количество изменённого тепла можно определить по формуле
Пример 2: Когда хлорид натрия растворяют в 100 г воды при 25°C, полученный раствор имеет температуру 21°C после надлежащего перемешивания. Если принять удельную теплоемкость раствора равной 4,18 Дж/г°С, рассчитайте изменение теплоты в процессе растворения.
Решение:
Здесь дано, что
c = 4,18 Дж/г°C,
m = 100 г,
ΔT = 25 – 21, 9 0007
т.
е. ΔT = 4 К
Процесс приводит к падению температуры, что указывает на то, что растворение соли имеет тенденцию к поглощению тепла из системы. Так как тепло, потерянное водой, такое же, как тепло, поглощенное солью,
Мы имеем,
Q = m × c × ΔT
Q = 100 × 4,18 × 4
Следовательно, Q = 1672 Дж
Пример 3: Когда 240 граммов железа охлаждаются с 90 °C до 25 °C, какое количество тепла выделяется? (Дано: с = 0,452 Дж/г °С).
Решение:
Имеем,
m = 240 г,
Удельная теплоемкость железа (c) = 0,452 Дж/г°C,
ΔT = Конечная температура – Начальная температура = 25 – 90 = -65 °C
У нас есть формула,
Q = m × c × ΔT
Подставляя данные значения в приведенное выше уравнение, мы получаем,
Q = 240 × 0,452 × (-65)
отсюда Q = -7051,2 Дж
т.е. Q = -7,05 кДж
Следовательно, 7,05 кДж при протекании процесса выделяется тепло.
Пример 4. При наличии 650 кДж энергии, сколько углерода можно нагреть с 20 градусов C до 100 °C? (Дано: c = 4,184 Дж/г °C)
Решение:
Здесь мы получаем,
c = 4,184 Дж/г °C,
q = 650 кДж = 650000 Дж
ΔT = 100 – 20 = 80 градусов Цельсия
Нас попросили найти массу (m), поэтому у нас есть формула,
Q = m × c × ΔT
приведенное выше уравнение даст нам,
m = Q / (c × ΔT)
, подставив данные значения в приведенное выше уравнение, мы получим фактическую массу необходимого углерода,
m = 650000 / (4,184 × 80)
m = 1941,9 г
т. е. m = 194 кг
Пример 5: Какова удельная теплоемкость 60 граммов вещества, которое нагревается от 30°C до 40°C при 968 Дж энергии добавилось?
Решение:
В вопросе указано, что
m = 60 г
ΔT = 40 – 30 = 10 градусов Цельсия
q = 968 Дж
Нам нужно найти удельную теплоемкость емкость ( c ), поэтому у нас есть формула
Q = m × c × ΔT
, приведенное выше уравнение даст нам
c = Q / (m × ΔT)
, подставив заданные значения в приведенное выше уравнение, мы получится,
с = 968 / (50 × 10)
c = 1,936 Дж/г°C
Теплоемкость и удельная теплоемкость
Термохимия
Теплоемкость и удельная теплоемкостьРазным объектам требуется разное количество тепла для повышения их температуры.
Например, если вы нагреете стакан со 100 г воды и 100-граммовую железную пластину, последняя достигнет высокой температуры намного быстрее, чем вода.
Это связано с тем, что называется теплоемкость (C) . Теплоемкость вещества — это количество теплоты, необходимое для повышения температуры данного количества вещества на один градус Цельсия. Возможны два случая, когда теплоемкость приводится к определенному количеству материала:
- Удельная теплоемкость (
Cs ) – количество теплоты, необходимое для повышения температуры 1 грамма вещества на 1°С. ( C или S часто используются вместо Cs для удельной теплоемкости).
- Молярная теплоемкость – это количество тепла, необходимое для повышения температуры 1 моля вещества на 1 °C.
Удельная теплоемкость показана взаимозаменяемо как C, C s или S .
Удельная теплоемкость железа и воды составляет 0,449 Дж/г · o С и 4,18 Дж/г · o С соответственно. меньшая теплоемкость железа означает, что ему требуется меньше тепла для повышения температуры на 1 o °С, чем воде.
Независимо от того, какой материал используется, экспериментально установлено, что изменение температуры прямо пропорционально теплу , поглощенному материалом: q ∝ Δ Т .
Константа пропорциональности между изменением температуры и поглощенным теплом есть теплоемкость:
Пример:
Проба воды массой 356 г нагревается с 15,0 °C до 84,0 °C. Рассчитайте количество теплоты, поглощенное водой (в килоджоулях).
Удельная теплоемкость железа составляет 0,449 Дж/г · o C, и все, что нам нужно сделать, это поставить цифры: = \;мС\Дельта Т\; = \,{\rm{356}}\;\cancel{{\rm{g}}}{\rm{ \times 0}}{\rm{.
3}\,{\rm{J}}\] 9{\rm{3}}}\,{\rm{J}}\,{\rm{\times}}\;\frac{{{\rm{1}}\;{\rm{kJ}}} }{{{\rm{1000}}\,{\rm{J}}}}\;{\rm{ = }}\;{\rm{11}}{\rm{.0}}\;{ \rm{kJ}}\]
Еще одна задача, связанная с теплоемкостью, – определение конечной температуры при смешивании проб горячей и холодной воды.
Например, ,
Какова конечная температура, когда образец воды весом 40 г при температуре 90 °C смешивается с образцом воды весом 60 г при температуре 25 °C?
При смешивании любых образцов при разных температурах система переходит к конечной температуре, которая находится между температурой горячих и холодных образцов. Происходит передача тепла от горячего образца к холодному:
В основе решения этой задачи лежит предположение, что потери тепла в окружающую среду отсутствуют, поэтому q получено = – q потеряно .
Теплота перетекает от более теплого образца (q потеряла ) к более холодному (q приобрела ), а количество тепла, потерянного более теплым образцом, равно количество тепла полученный более холодным образцом.
Мы также можем записать теплопередачу как q потеряно + q получено = 0 или
q 1 + q 2 = 0
Для нашей задачи q 1 = mCΔT 1 , q 2 = mCΔT 2
так, m 1 CΔ T 1 + m 2 CΔT 2 = 0
Присвоим «1» для обозначения более теплой пробы воды и «2» для более холодной пробы. Тогда изменения температуры будут:
ΔT 1 = T f – 90 и ΔT 2 = T f – 25
Где T f — конечная температура системы, поэтому она одинакова. для червячных и холодных образцов.
Подставьте числа и найдите T f в следующем уравнении: 25) = 0
Потому что C (теплоемкость воды) появляется в обеих частях уравнения и может быть сокращена.
40 г x (T f – 90) + 60 г x (T f – 25) = 0
T f = 51 °C
Обратите внимание, что уравнение также можно настроить с помощью Кельвина (K).
Кофейная чашка из пенополистирола содержит 150 граммов воды при температуре 23,0 o C
. 45,0-граммовый блок металлического серебра нагревают до 100,0 o C и затем помещают в воду в чашке. Содержимое чашки доходит до конечной температуры 24,3°С.0064 или C . Какова удельная теплоемкость серебра?
Вспомните еще раз все задачи по термохимии основаны на принципе, что теплота не теряется, а только перетекает от объекта с более высокой температурой к более холодному:
Второе выражение для сложения потерянного и полученного тепла проще в использовании, потому что вам не нужно запоминать, какое из них имеет отрицательный знак.
Итак, что мы делаем, так это пишем формулу, коррелирующую теплоемкость и теплоемкость для образцов воды и серебра, складываем их, чтобы получить ноль: 0243 С x (24,3 o
C – 23,0 o C ) + 45 г ( X 9024 3 Дж/г o C) x (24,3 o C) – 100,0 о С ) = 0 q (вода) q (серебро)
9 0007
Запишем уравнение без единиц измерения:
250 х 4,18 х (24,3 – 23,0) + 45 ( х) х (24,3 – 100,0) = 0
15236,1 – 14421 + 1093,5Х – 4500Х = 0
815,1 – 3406,5Х = 0
Х = 815,1/3406,5 = 0,239
Следовательно, расчетная удельная теплоемкость серебра равна 0,239 Дж/г o C .
Практика
1.Сколько теплоты потребуется для повышения температуры образца Fe массой 540,6 г с 20,0 °C до 84,3 °C? Удельная теплоемкость железа = 0,450 Дж/г°С.
{{\rm{3}}\;}}{\rm{J}} \]Чтобы преобразовать Дж в кДж, нам нужно разделить его на 1000, то есть 15,6 кДж
2.Рассчитайте удельную теплоемкость металла, если для образца массой 17,0 г требуется 481 Дж для изменения температуры металла с 25,0 °С до 67,0 °С?
ответ
0,674 Дж/г°C
Решение
Переформулируем следующее уравнение для зависимости теплоемкости, удельной теплоемкости и изменения температуры: 9{\rm{o}}}{\rm{C}}}}\;\]
3.Рассчитайте энергию сгорания одного моля бутана, если при сжигании пробы бутана массой 0,367 г (C 4 H 10 ) температура калориметрической бомбы увеличилась на 7,73 °C. Теплоемкость бомбового калориметра 2,36 кДж/°С.
ответ
2,875 кДж/моль
Раствор
Поскольку при сгорании бутана температура в бомбовом калориметре повышается, это экзотермическая реакция.
Это означает, что теплота переходит от реакции в калориметр и при отсутствии потерь тепла теплота, выделяемая реакцией, равна теплу, поглощаемому калориметром: -q реакция = q кал
Так как реакция происходит в условиях постоянного объема, q rxn = ΔE rxn, поэтому нам нужно рассчитать q кал по следующей формуле:
q кал = C кал x ΔT
q кал = 2,36 кДж/ °C x 7,73 °C = 18,2 кДж
Следовательно, q rxn = -18,2 кДж
Это изменение внутренняя энергия реакции для того конкретного количества бутана, которое было сожжено.
Чтобы получить ΔE rxn на моль бутана, нам нужно разделить q rxn на количество молей, которые фактически прореагировали. Чтобы найти число молей, используем мас и молярную массу бутана:
n(C 4 H 10 ) = 0,367 г/58,0 г/моль = 0,00633 моль
. После этого делим теплота реакции на количество молей бутана, чтобы получить теплоту реакции на моль бутана:
ΔE rxn = 18,2 кДж/0,00633 моль = 2,88 x 10 3 кДж/моль
В качестве альтернативы можно установить корреляцию перекрестного умножения:
0,00633 моль C 4 H 10 – 18,2 кДж
1 моль C 4 H 10 – X кДж
X = 2,88 x 10 3 кДж/моль
4.Сколько джоулей энергии требуется, чтобы растопить 40,0 г льда при 0 °С? Теплота плавления (Δ H плавка ) для льда составляет 334,0 Дж/г.
ответ
13,360 Дж
Решение
Так как лед/вода уже имеет температуру 0 o C (температура плавления/замерзания), добавленное тепло не изменяет температуру смеси льда и воды, а скорее используется для перехода из твердого состояния в жидкое.
Для расчета количества энергии, необходимой для достижения изменения состояния, в данном случае плавления, вещества, которое уже находится при температуре изменения состояния, мы используем следующую формулу:
q = mΔ H fus
где q — количество тепловой энергии, m — масса, а Δ H fus — энтальпия плавления, иногда называемая теплотой плавления. Это энергия, необходимая для сплавления (расплавления) грамма (или моля) вещества.
Подставив числа в формулу, получим:q = 40,0 г x 334,0 Дж/г = 13 360 Дж
Округлив до трех значащих цифр, получим q = 1,34 x 10 3 Дж
5.Сколько кДж энергии потребуется, чтобы превратить 36,0 г льда при -15,0°C в воду при 0°C ? Удельная теплоемкость льда составляет 2,10 Дж/г°С, а теплота плавления (Δ H fus ) для льда составляет 334,0 Дж/г.
ответ
13,2 кДж
Решение
В предыдущей задаче мы упоминали, что, поскольку лед/вода уже находится при температуре 0 o C (температура плавления/замерзания), добавленное тепло не изменяет температуру смесь льда и воды, а скорее используется для перехода из твердого состояния в жидкое. Здесь это не так, потому что лед имеет температуру -15,0 oC и перед тем, как растаять, его нужно сначала нагреть до 0, o C. Следовательно, в этом процессе есть две стадии; 1) нагрев льда до 0 o С, 2) таяние льда.
Тогда общая теплота этого процесса равна:
q = q нагрев + q плавление
q нагрев рассчитывается по формуле, которую мы уже использовали несколько раз:
q отопление = м × C × ΔT
\[{{\rm{q}}_{{\rm{нагрев}}}}\;{\rm{ = }}\;{\rm{36}}{\rm{.

 е. ΔT = 4 К
е. ΔT = 4 К
 Например, если вы нагреете стакан со 100 г воды и 100-граммовую железную пластину, последняя достигнет высокой температуры намного быстрее, чем вода.
Например, если вы нагреете стакан со 100 г воды и 100-граммовую железную пластину, последняя достигнет высокой температуры намного быстрее, чем вода.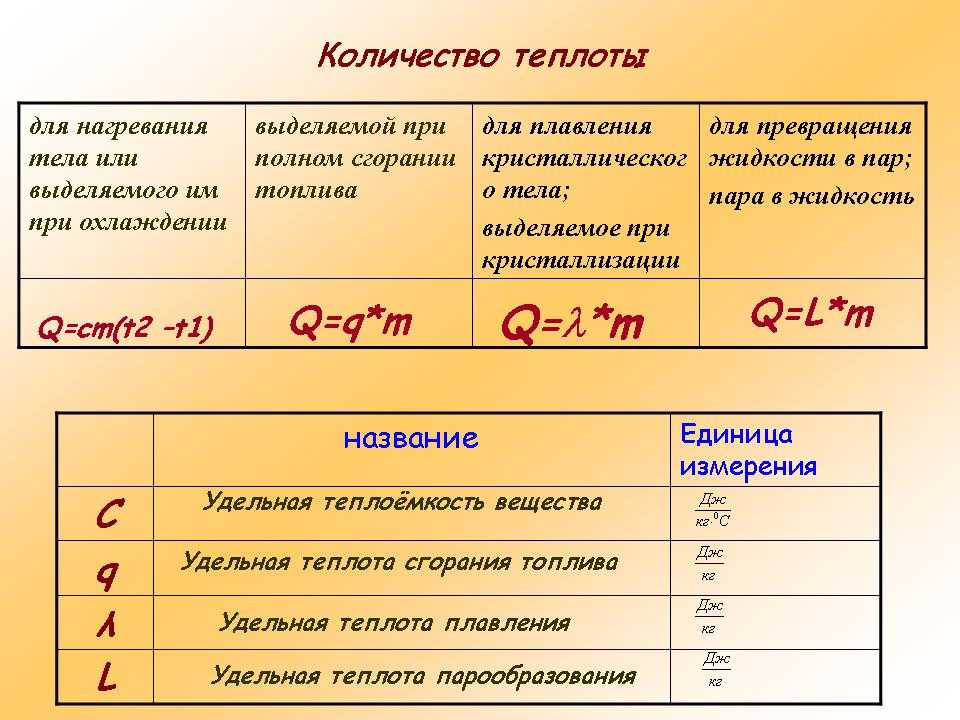
 3}\,{\rm{J}}\] 9{\rm{3}}}\,{\rm{J}}\,{\rm{\times}}\;\frac{{{\rm{1}}\;{\rm{kJ}}} }{{{\rm{1000}}\,{\rm{J}}}}\;{\rm{ = }}\;{\rm{11}}{\rm{.0}}\;{ \rm{kJ}}\]
3}\,{\rm{J}}\] 9{\rm{3}}}\,{\rm{J}}\,{\rm{\times}}\;\frac{{{\rm{1}}\;{\rm{kJ}}} }{{{\rm{1000}}\,{\rm{J}}}}\;{\rm{ = }}\;{\rm{11}}{\rm{.0}}\;{ \rm{kJ}}\]