Технология монтажа перегородок из ГКЛ

Инструменты для работы:

• уровень лазерный,
• ножницы по металлу,
• электродрель.

Материалы для работы:

• направляющая размером 50х40 мм,
• профиль 50х50 мм,
• соединительный элемент,
• пресс шайбы для соединения,
• саморезы по металлу 35 мм,
• подвес П-образного типа,
• веревка, ГКЛ.

Разметка

Используя разметочный шнур, нужно задать разметку на полу. Она будет указывать ось установки перегородки. Также нужно будет отметить расположение дверных проемов. Затем, используя трассировочный шнур и отвес, нужно перенести полученную разметку на стену и потолок.

Установка направляющих для гипсокартонной перегородки

На тыльную сторону направляющих потребуется приклеить звукоизолирующую ленту. После этого они крепятся по намеченной оси на полу и на потолке. На месте расположения дверей делается промежуток. Крепление производится пластмассовыми дюбелями размером 6×40, 6×60 или 8×60 мм. На одном отрезке профиля должно находиться не менее трех дюбелей для получения устойчивости и надежности конструкции.

Установка стоек для гипсокартона

Существует два способа монтажа: немецкий и американский. Согласно немецкой технологии установка профилей-стоек производится сначала в профиль, расположенный на полу, после этого верхний конец стойки вставляется в направляющую, закрепленную на потолке, куда она должна заходить не менее, чем на 20 мм. После этого проводится выравнивание профилей по оси с использованием шага не менее 600 мм. У профиля-стойки открытая поверхность должны быть направлена в сторону гипсокартонной плиты. В американском варианте в сторону гипсокартона должен быть обращен только профиль, расположенный вдоль стены.

Установка первой гипсоартонной стены

Начинается монтаж с установки гипсокартона шириной в 1200 мм. В качестве крепежа нужно взять саморезы для металла, имеющих длину в 25 мм.

Они вкручиваются на расстоянии 250 мм друг от друга. Если предполагается сделать обшивку перегородки в два слоя, то шаг следует сделать в 750 мм. При этом нужно произвести смещение шва между листами гипсокартона размером в один шаг на 600 мм. Монтаж второго слоя гипсокартона в этом случае должен начинаться с листов, имеющих ширину 600 мм. Такие листы крепятся с помощью саморезов по металлу длиной в 35 мм на расстоянии 250 мм.

Монтаж изоляционного слоя внутри гипсокартнонной перегородки

Установив обшивку с одной стороны, нужно будет начать прокладку коммуникаций внутри перегородки. После ее завершения необходимо уложить изоляционный слой из стекловаты или минваты. Изоляционный слой не должен сползать и полностью должен заполнять пространство внутри перегородки.

Установка второй стены для перегородки

При установке следующей стороны необходимо сместить на 600 мм вертикальный шов между гипсокартонными плитами, ориентируясь на обшивку первой стороны перегородки. Первыми устанавливаются плиты шириной в 600 мм. Если проводится двойная обшивка, установка второго слоя должна начинаться с сегмента гипсокартона, имеющего ширину 1200 мм.

Пошаговая технология монтажа прямой и произвольной перегородки из гипсокартона:

1. Производится разметка по полу, стене и потолку в месте установления перегородки для последующего крепления направляющих для гипсокартона.
2. Проводится установка каркаса для перегородки с помощью креплений и профилей. Полученная в ходе его конструкция должна повторять в точности разработанный проект технического задания. Если монтируется отдельно стоящая конструкция, то необходимо увеличить количеств отточек крепления на потолке для большей прочности конструкции. В качестве крепежа в отдельно стоящих произвольных конструкциях можно использовать специальные декоративные детали в виде труб, стоек или других элементов.
3. Производится прокладка проводки к местам выхода электрического кабеля, если это указано в техническом задании.
4. Проводится обшивка каркаса перегородки плитами из гипсокартона.
5. Проведение выравнивания углов и последующая покраска рабочими смесями гипсокартонных стен.
6. Финишные отделочные работы, для которых можно использовать краску, обои или другие отделочные материалы.
7. Установка розеток и осветительного оборудования в указанных техническим заданием местах.

Как проверить качество выполненных работ по установке перегородки из гипсокартона

Двухметровая рейка, приложенная к поверхности готовой перегородки, должна лежать достаточно плотно. Допустимо не более двух неровностей на высоте в два метра или на глубину не более 3 мм. При вертикальной проверке отвесом или уровнем отклонение не должно быть более 2 мм для 1 метра высоты перегородки и не более 1 см на всю ее высоту (h).

При монтаже двухслойной перегородки нельзя устанавливать друг против друга стыки листов гипсокартона.

Нельзя располагать друг против друга крепеж из винтов и шурупов смежных листов на одной и другой стороне перегородки.

Принимая готовую работу, нужно обратить внимание НАТО, чтобы:

• каркас был устойчив и не качался;
• листы гипсокартона были надежно и правильно прикреплены к каркасу перегородки;
• на листах не должно быть повреждений в виде сколов, надрывов, трещин, пятен, надломов и грязи;
• угловые элементы должны иметь строго 90^0.

Специфика монтажа:

Для встроенных шкафов перегородка должна иметь прямые углы и ровную заднюю стенку. Торцы перегородки нужно устанавливать, ориентируясь на лазерный уровень. Вверху и внизу ширина перегородки от стены должна быть одинакового размера.

Чтобы получить качественную поверхность из гипсокартона нельзя в качестве крепежных материалов использовать саморезы для крепежа ПН и ПС. Необходимо в данном случае проводить крепление с помощью просекателя. Спрятанные в стену батареи центрального отопления следует одеть в подходящий изоляционный материал, например, во вспененный полиэтилен.

Расчет материалов на 1м²

Наименование	Ед. изм.	Норма расхода	Расчетное количество
КНАУФ-лист (ГКЛ, ГКЛВ, ГКЛО)	м2	0,7	0,7
Профиль направляющий UW 50/40 (75/40, 100/40)	м.п.	1,1	1,1
Профиль стоечный CW 50/50 (75/50, 100/50)	м.п.	2	2
Шуруп самонарезающий TN 25	шт.	17	17
Дюбель ‘К’ 6/40	шт.	1,6	1,6
Лента уплотнительная	м.п.	1,2	1,2
Серпянка самоклеющаяся 5смх45м	м2	2,2	2,2

Карта объектов Более 10 000 объектов

Смотреть карту

Спасибо за обращение!

С вами свяжутся в ближайшее время

устройство межкомнатных конструкций серии C112 из гипсокартона

В ремонтных и строительных работах применим гипсокартон и его комплектующие.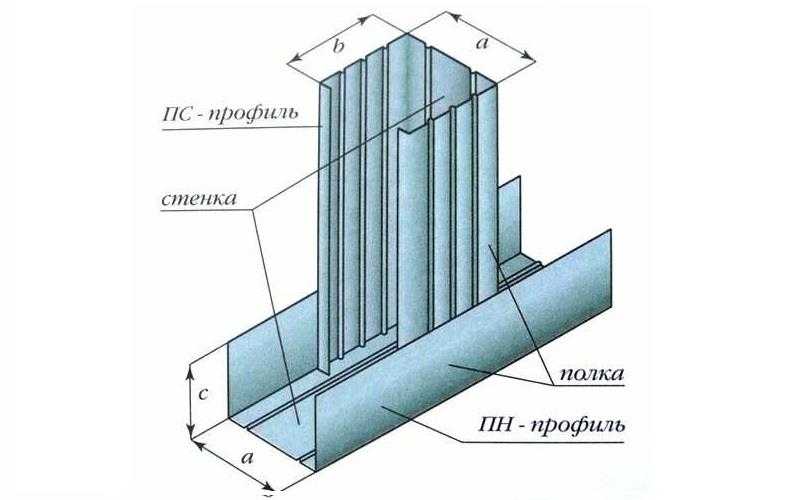 Этот строительный материал имеет ровную поверхность, поэтому можно с лёгкостью выровнять стены с помощью ГКЛ, создать фигурные многоуровневые потолки, а также разделить комнату на две при помощи перегородок. Перегородки Кнауф из пазогребневого гипсокартона имеют множество плюсов. Функциональность перегородки в основном направлена на разделение помещения.

Вернуться к оглавлению

Полное содержание материала

• 1 Плюсы использования технологии Кнауф
• 2 Типы перегородок и особенности монтажа
• 3 Перегородка С112
  • 3.1 Монтаж перегородки С112
  • 3.2 Обшивка гипсокартоном перегородки С112
• 4 Перегородка С361
• 5 Перегородка С365
• 6 Перегородка W118
• 7 Факторы, влияющие на выбор перегородки

Плюсы использования технологии Кнауф

Сборные гипсокартонные системы перегородок Кнауф применяются как в квартирах, так и в общественных местах. Они имеют отличия по типам, размерам. С их помощью создаются стены и перегородки.

Сборка каркаса перегородки кнауф

Главным преимуществом, является материал Кнауф. Пазогребневые гипсоплиты созданы по литиевой технологии.

Необходимое количество материалов для монтажа перегородки

Они не горят и являются огнестойкими. Составные плиты не содержат ядовитых примесей, вредных для человека и животного. Такие плиты легко монтируются, поддаются обработке.

1. В данной системе используются комплектующие высокого качества. Для этого есть специальный отдел Кнауф, следящий за качеством выпускаемой продукции.
2. Расчет материала проходит легко, без затруднительных составлений математических формул и их вычитания.
3. Для каждой системы выпускается подробная инструкция для сборки гипсокартонной перегородки.
4. Для создания перегородки из гипсокартона самостоятельно, идёт закупка множества материалов. В готовой системе не требуется в отдельности покупка профилей для гипсокартона или крепежей.

Гипсокартонные перегородки Кнауф отличаются полной комплектацией, что немаловажно в монтаже перегородки и её дальнейшего использования.

Вернуться к оглавлению

Типы перегородок и особенности монтажа

Фирма Кнауф выпускает перегородки отличные своими размерами и типами. Они для удобства различия делятся на модели.

Схема устройства и конструкция перегородки кнауф

По конструкции перегородки Кнауф делятся на количество слоёв гипсокартона (ПГП):

1. Один слой гипсокартона.
2. Два слоя.
3. Три слоя ГКЛ.
4. Один слой влагостойкого гипсокартона на одном каркасе.
5. Комбинированный гипсокартон с одной стороны и двухслойный – вторая сторона.
6. Трёхслойная обшивка влагостойкого ГКЛ и металлические листы.

В конструкции перегородок есть каналы для коммуникаций, а также выделенные места для вентиляции.

По каркасу Кнауф перегородки есть: однокаркасные, предназначенные для мест, где не надо сильная звукоизоляция и не будет сильного утяжеления конструкции. Двухкаркасные конструкции – прочные межкомнатные стены из гипсокартона, на которую можно повесить телевизор на гипсокартон или использовать как основу под создание мебели.

Вернуться к оглавлению

Перегородка С112

Система Кнауф С112 это состав материалов, которые создают перегородку с двухслойной обшивкой и одним металлическим каркасом.
Особенности перегородки:

• каркас сделан из металлических профилей и обшит с 2 сторон двумя слоями гипсокартона;
• при помощи создаваемого изделия решается важная задача – разграничение комнаты на зоны;
• монтаж гипсокартонной перегородки производится без применения «мокрых» методов;
• поверхность изделия является огнеупорной;
• возможность создания дизайнерского решения;
• готовую перегородку можно покрыть любым материалом: обои, краска, плитка;
• при создании перегородки улучшается теплоизоляция, а также звукопроницаемость.

Учитывая все особенности Кнауф, можно с уверенностью сказать – срок эксплуатации её продолжительный.

Названия элементов перегородки кнауф

Монтаж перегородки С112

Технология монтажа перегородки проводится с соблюдением пошаговой инструкции. Начинать монтажные работы следует проводить тогда, когда окончены все работы с электричеством и прокладкой всех кабелей под гипсокартоном. После окончания ремонтных работ с половым покрытием, а также окончание водных процедур в требуемом помещении.
Монтаж перегородки кнауф проводится следующим образом:

1. При помощи лазера и обивочного шнура на чистую поверхность пола, стен и потолка наноситься разметка.
2. На линиях отмечаются точки расположения стоечных профилей, а также дверной проём.
3. Первыми крепятся направляющие профили. Для отрезания профиля нужной длины используются ножницы для резки металла.
4. Для улучшения звукоизоляции на НП требуется приклеить уплотнительную ленту, согласно ширине профиля.
5. С помощью дюбелей 35 мм профиль крепится к полу. Шаг крепления не больше 1 метра.
6. Аналогично НП крепиться на потолочном перекрытии.
7. После этого следует измерить длину стоечного профиля от потолка до пола.

   Пример крепления стоечных профилей

8. Длина стоечного профиля должна быть на 1 см меньше, чем высота помещения.
9. На стоечные профили, которые крепятся к стене, наклеивается уплотнительная лента.
10. Если стена из гипсокартона Кнауф, тогда профили крепятся саморезами. Если кирпич или блок из ячеистого бетона, тогда применяются дюбели длиной 35 мм. Шаг крепления дюбелей или саморезов не больше 1 метра.

    Схема крепления листов гипсокартона Кнауф

11. Для дверей, весом 35 кг требуется смонтировать двойной стоечный профиль, методом насадки одного профиля на другой.

    Схема устройство двойного стоечного профиля

12. Монтируются стойки для дверей в направляющих профилях и крепятся саморезами длиной 9 мм.
13. Из направляющего профиля вырезается горизонтальная перемычка для двери. Устанавливается между стоечными профилями двери, вверху по высоте двери и крепится саморезами 9 мм.
14. От получившейся дверной коробки до потолка следует установить вырезанный стоечный профиль в количестве двух штук. Эти стойки крепятся методом просечки с вгибом.Схема соединения стоек

15. От пола до потолка устанавливаются стоечные профили через каждых 60 см, фиксация производится методом просечки.

    Чертеж с размерами для монтажа стоечных профилей

16. Спинки профилей должны быть отвёрнуты в одну сторону, а отверстия для кабелей находились на 1 уровне.

Обшивка гипсокартоном перегородки С112

После смонтированного металлического каркаса начинается обшивка ГКЛ. Лист от пола должен крепиться на расстоянии 1 см. При необходимости разрезания листа гипсокартона необходимо использовать строительный нож. Разрезается по намеченной линии картон и надламывается гипс.

С другой стороны картон следует отрезать по получившейся линии сгиба. Обрезанная часть ГКЛ обрабатывается и создаётся фаска 22 градуса. А также для отрезания листа используются резаки – малый (ширина отрезаемого листа 12 см), большой резак-63 см.

Монтаж гипсокартона производится при помощи специального устройства. Листы прижимаются к каркасу и крепятся шурупами. Они должны быть на одинаковом расстоянии друг от друга – 7.5 см, а также от края на расстоянии не больше 15 см. Головка шурупа должна быть утопленной в ГКЛ на 1 мм.

В месте, где соединяются 2 листа по вертикали, следует установить перемычку из профиля. Соседние горизонтальные стыки смещаются на 40 см.

После монтажа гипсокартонных листов, через отверстия в металлических стойках следует протянуть провода электричества и другие кабели.

Пример монтажа проводки под гипсокартоном

Следующим шагом является укладка изоляционного материала кнауф инсулейшн с открытой стороны перегородки. И обшивка перегородки гипсокартонными листами. Но, стыки гипсокартона с одной стороны не должны совпадать со стыками с другой стороны. Таким способом создаётся прочность конструкции.

Окончательным шагом в первом уровне является заделка швов гипсокартона. Для этого следует стыки с самодельной фаской на гипсокартоне и обработать ГКЛ грунтовкой . После чего требуется сделать раствор для заделки стыков из сухой смеси Кнауф Унифлот. Шпаклёвка равномерно наносится на стыки узким шпателем 15 см.

Процесс шпаклевки перегородки из гипсокартона

После шпатлевания следует приступить к монтажу второго уровня гипсокартона. При этом стыки первого слоя гипсокартона не должны совпадать со вторым уровнем гипсокартонного покрытия перегородки.
При помощи специального оборудования на намеченных точках требуется вырезать отверстия для электрокоробок под выключатель и розетки в гипсократоне.

Высверливание отверстия под розетки

Стыки второго слоя гипсокартона требуется заделать при помощи армирующей ленты Кнауф. После высыхания шпатлевки на стыках с армирующей лентой требуется сделать затирку от лишних кусочков.
После выполнения затирки всю поверхность следует прогрунтовать «Кнауф Тифенгрунд».

Подробный процесс монтажа отверстий в гипсокартоне под розетки

Если перегородка будет покрашена, тогда перед покраской всю поверхность следует прошпаклевать «Кнауф Мульти-Финиш». Когда поверхность высохнет, её следует затереть и покрыть грунтовкой.

Смотрите в видео процесс монтажа перегородки Кнауф.

Вернуться к оглавлению

Перегородка С361

Эта перегородка сделана из одинарного каркаса и обшита с двух сторон одним слоем влагостойкого гипсокартона. В состав этой системы входит влагостойкий гипсокартон – 12.5 см, а также наполнитель – минеральная вата.

Схема с размерами перегородки с361

Влагостойкая перегородка ставится в ванной комнате и в помещении с повышенной влажностью. Для установки перегородки должна быть температура не ниже +10 градусов. Перегородка в собранном виде имеет вес 18 кг. Это большой плюс для квартир, где нельзя утяжелять несущие стены, а также иные гипсокартонные конструкции.

Вернуться к оглавлению

Перегородка С365

Эта перегородка сделана из двойного каркаса, с двух сторон обшита двойным влагостойким ГКЛ. Стойки металлического каркаса обклеиваются специальной лентой для звукоизоляции. Наполнителем выступает минеральная вата, которая укладывается в 2 -3 слоя.

Эта конструкция служит прочной стеной с высокими показателями звукоизоляции, прочности.

Вернуться к оглавлению

Перегородка W118

Перегородка имеет 3 слоя гипсокартона. Но, между гипсокартоном монтируется оцинкованный лист, толщиной 0.5 мм. Этот тип перегородки следует устанавливать в строгом соответствии с техническими характеристиками материала, а также с инструкцией по установке.

Схема устройства перегородки W118

Металлический каркас перегородки усилен профилем ПС 100. Толщина его – 0.6 мм.

Вернуться к оглавлению

Факторы, влияющие на выбор перегородки

Фирма Кнауф предлагает большой выбор перегородок. И каждая из них уникальная по-своему. Каждая перегородка предназначена для разных помещений, с разной температурой и уровнем влажности.
Прежде чем приобрести систему перегородки Кнауф следует обратить внимание:

1. Высота комнаты, где будет монтироваться перегородка.
2. Насколько шумно в помещении, и следует ли убрать этот шум? Если да, тогда требуется кнауф акустическая перегородка.
3. Нагрузка на несущие стены или стена, выровненная гипсокартоном.

   Каркас гипсокартонной перегородки Кнауф

4. Состояние базовой стены.
5. Необходимость сокрытия коммуникаций коробом в перегородке.
6. Будет ли в перегородке дверь.
7. Высота самой конструкции – будет она до потолка или декоративный элемент интерьера помещения.

   Схема крепления гипсокартонной перегородки к стене

8. Температурный режим.
9. Какие функции будет выполнять перегородка.

Схема обшивки перегородки листами гипсокартона

Выбирая перегородку Knauf, следует все обдумать. Ведь эта конструкция должна вписываться в помещение, а не стать преградой для живущих там людей. Интерьер квартиры должен подчёркивать зонирование комнаты. Перегородку можно снабдить подсветкой, покрыть краской или обклеить обоями. По желанию в перегородке можно сделать сквозные окна или ниши для декора.

Repartition vs repartition on read — Hail Query & hailctl

ch-kr 9 марта 2022 г., 16:41 1

Привет, команда!

Насколько я понимаю, переразметка таблицы при чтении ( hl.read_table(path, _n_partitions=n_partitions) ) лучше, чем запуск ht.repartition(n_partitions) . Однако я заметил, что перераспределение таблицы при чтении не увеличивает количество разделов во входной таблице до желаемого числа, а запускает 9 разделов.0009 ht.repartition() правильно увеличивает количество разделов.

Например:
Это схема ввода таблицы

 ---------------------------------- ------
Тип файла: Таблица
    Разделов: 4906
    Ряды: 100
    Пустые разделы: 4806
    Мин. (строки/раздел): 0
    Макс (строки/раздел): 1
    Медиана (строки/раздел): 0,0
    Среднее (строки/раздел): 0
    StdDev (строки/раздел): 0
----------------------------------------
Глобальные поля:
    'мин_размер_окна': int32
----------------------------------------
Поля строки:
    'стенограмма': ул.
    'total_oe': float64
    'max_idx': int32
    'транскрипт_старт': int32
    'конец стенограммы': int32
    'cum_obs': массив  
    'cum_exp': массив 
    'позиции': массив 
    'list_len': int32
----------------------------------------
Ключ: ['стенограмма']
----------------------------------------
 

и это код, который я запускаю:

 ht = hl.read_table('gs://gnomad-tmp/kc/test_100_over5k.ht')
split_window_size = 500
ht = ht.filter (ht.transcript == 'ENST00000217939')
ht = ht.annotate(
    start_idx=hl.flatmap(
        лямбда i: hl.map(
            лямбда j: hl.struct(i_start=i, j_start=j),
            hl.range(0, ht.list_len, размер_разделенного_окна),
        ),
        hl. range(0, ht.list_len, размер_разделенного_окна),
    )
)
ht = ht.explode("start_idx")
ht = ht.annotate (i = ht.start_idx.i_start, j = ht.start_idx.j_start)
ht = ht._key_by_assert_sorted («расшифровка», «i», «j»)
ht = ht.filter (ht.j >
 = ht.i)
ht = ht.annotate(
    i_max_idx=hl.min(ht.i + 500, ht.list_len - 1),
    j_max_idx=hl.min(ht.j + 500, ht.list_len - 1),
)
ht = ht.annotate(
    start_idx=ht.start_idx.аннотировать(
        j_start=hl.if_else(
            ht.start_idx.i_start == ht.start_idx.j_start,
            ht.start_idx.j_start + 1,
            ht.start_idx.j_start,
        ),
    ),
)
n_rows = ht.count()
печать (n_строки)
 

оператор печати здесь печатает 120.

Running

 ht.write('gs://gnomad-tmp/kc/mxra5_rep_on_read_test.ht', overwrite=True)
ht = hl.read_table('gs://gnomad-tmp/kc/mxra5_rep_on_read_test.ht', _n_partitions=n_rows)
ht.n_partitions()
 

отпечатков 20 .

Однако работает

 ht = ht.repartition(n_rows)
ht = ht.  checkpoint('gs://gnomad-tmp/kc/mxra5_repart_test.ht', перезаписать = True)
ht.n_partitions()
 

отпечатков 120 .

Есть ли причина, по которой перераспределение таблицы при чтении приводит к перераспределению этой таблицы только на 20 разделов? Буду признателен за любую информацию – заранее спасибо!

Редактировать — вот лог приветствия:
repartition_test.log (1,1 МБ)

tpoterba 15 марта 2022 г., 18:35 2

У вас есть только 100 строк — многие операции секционирования имеют небольшой шум/ошибку, когда количество строк близко к количеству секций. В частности, не следует ожидать, что повторное разбиение на большее количество разделов, чем количество строк, приведет к такому количеству разделов (включая пустые разделы). Я не думаю, что это то, о чем стоит сильно беспокоиться — есть ли причина, по которой вам нужно больше 20 разделов?

ч-кр 15 марта 2022 г. , 18:47 3

спасибо за ответ! да, причина, по которой я пытаюсь увеличить количество разделов, заключается в том, что я запускаю hl.experimental.loop в каждой строке таблицы, и я понимаю, что большее количество разделов ускорит операция цикла

Исай Шур, Генри Олдер и разделы — МАТЕМАТИЧЕСКИЕ ЗНАЧЕНИЯ

Автор: Дэвид Брессоуд @dbressoud

Дэвид Брессоуд — почетный профессор ДеВитта Уоллеса в Макалестерском колледже и бывший директор Конференционного совета по математическим наукам

MAA только что опубликовал Решение проблем предварительного исчисления с помощью последовательности исчисления II с помощью тематических исследований , том «Примечания», обобщающий результаты проекта, спонсируемого NSF, «Прогресс через исчисление» , тематические исследования вмешательств в последовательность «Предварительное исчисление через исчисление II» . Он доступен по адресу https://www.maa.org/sites/default/files/pdf/pubs/books/members/NTE92.pdf . Введение с описанием исследования и содержанием этого тома доступно по адресу https://macalester.edu/~bressoud/misc/PtC-Introduction.pdf.

Задача: Докажите, что количество способов записать целое число в виде суммы целых чисел, сравнимых с +1 или –1 по модулю 6, равно количеству способов записать это целое число в виде суммы различных целых чисел. не менее чем на 3, причем кратные 3 отличаются не менее чем на 6.

Например, есть шесть разделов из 12, которые удовлетворяют первому ограничению: 11+1, 7+5, 7+1+1+1+1 +1, 5+5+1+1, 5+1 +1+1+1+1 +1+1 и 1+1+1+1+1+1+1+1+1+1+1+ 1. Есть также шесть разбиений на 12, которые удовлетворяют второму: 12, 11+1, 10+2, 9.+3, 8+4 и 7+3+1.

 

Несколько слов об этой проблеме, прежде чем я перейду к своей истории: Эйлер показал, что количество способов записать целое число в виде суммы нечетных целых чисел (конгруэнтных +1 или –1 по модулю 4) равно количество способов записи этого числа в виде суммы различных целых чисел (отличающихся не менее чем на 1). Как представлено в моей последней колонке, тождества серии q , открытые независимо Л. Дж. Роджерсом и С. Рамануджаном, подразумевают, что количество способов записи целого числа в виде суммы целых чисел, конгруэнтных +1 или –1 по модулю 5, равно количество способов записать это целое число в виде суммы целых чисел, отличающихся не менее чем на 2. Равенство, данное в задаче, обнаруженной Иссаем Шуром в 1926, кажется, попадает в эту схему. Шур наиболее известен своими работами в области теории представлений, но он также внес значительный вклад в комбинаторику и теорию чисел, включая теорию разделов, где он независимо открыл тождества Роджерса-Рамануджана.

Исай Шур (1875–1941)

Возникает искушение попытаться распространить эти тождества на модуль 7. Кажется, что ничто сравнимое не работает ни там, ни для любого большего модуля. Это яркий пример 9-й модели Ричарда Гая.0075 сильный закон малых чисел : «Недостаточно малых чисел, чтобы удовлетворить множество предъявляемых к ним требований». Тот факт, что закономерность проявляется в нескольких небольших случаях, не обязательно означает, что она продолжается. Как обнаружил Бэзил Гордон в 1961 году и как я объясню позже в этой колонке, плодотворное обобщение на более высокие модули было связано не с тем, какие классы вычетов сохраняются, а скорее с точки зрения того, какие классы вычетов исключаются.

Генри Алдер (1922–2002)

В 1956 году Генри Алдер выдвинул гипотезу о более слабом расширении теоремы Шура, согласно которой количество разбиений n на части, отличающиеся по крайней мере на d , всегда больше или равно количеству разбиений n на части, конгруэнтные +1 или –1 по модулю d +3. В 1971 году Джордж Эндрюс доказал это для случаев, когда d на единицу меньше, чем степень числа 2. В 2004 году Э Джа Йи установил истинность этой гипотезы для всех d больше 31. Остальные случаи были доказаны в 2011 году Клаудией Алфес, Мари Джеймсон и Робертом Дж. Лемке Оливером. См. ссылки в конце этой колонки.

Генри Алдер был преподавателем Калифорнийского университета в Дэвисе. Он был секретарем МАА с 1960 по 1975 год и президентом с 1977 по 1979 год. Я включил теорему Шура, потому что в самом начале своей карьеры я обнаружил простое доказательство, настолько привлекательное, что Генри Алдер в своем выступлении на пенсию в качестве президента МАА включил его в свою разговаривать. Я прибыл.

Я возвращаюсь к своей истории лета 1976 года. Была найдена основная часть результатов, которые легли в основу моей докторской диссертации. Гроссвальд порекомендовал мне посетить летние математические собрания, которые проводились в том же году в Университете Торонто, чтобы рассказать о своих открытиях. Это был незапрошенный 10-минутный разговор от совершенно неизвестного, что обычно является признаком того, что будет довольно небольшая аудитория. Что еще хуже, моя презентация противоречила последней презентации Аппеля и Хокина их доказательства теоремы о четырех цветах, компьютерного доказательства того, что любую плоскую карту всегда можно раскрасить четырьмя цветами без необходимости двух смежных областей. разделяют тот же цвет.

Насколько я помню, в аудитории на моем выступлении было три человека: человек, который говорил передо мной и которому нужно было представить мое выступление, человек, который должен был говорить после меня и который нервно ждал своей очереди, и Дик Аски .

Дик просмотрел рефераты и выбрал мою работу как демонстрирующую потенциал. Затем он провел со мной остаток дня, объясняя, как моя работа связана с теорией серии q , и рассказывая мне, что мне нужно прочитать, особенно книгу Джорджа Эндрюса «9».0075 The Theory of Partitions , вышедшей в 1976 году, и Theory and Applications of Special Functions , сборник статей, представленных в 1976 году на специальном семинаре в Университете Висконсина. В частности, он направил меня к статье Джорджа Эндрюса «Проблемы и перспективы основных гипергеометрических функций», которую я приступил к подробному изучению.

Дик тоже считал, что мне будет полезно познакомиться с Джорджем. Я точно не знаю, как это произошло. Гроссвальд знал Эндрюса. У них был один и тот же научный руководитель Ганс Радемахер. Они пересекались в Пенне, где Джордж был аспирантом, а Гроссвальд — инструктором, и знали работы друг друга. Для Гроссвальда было вполне естественно пригласить Эндрюса, который находился недалеко от Пенсильванского университета, приехать в Темпл, чтобы представить коллоквиум, что он и сделал в начале 19-го века.77. Дик, который был очень близок с Джорджем, мог внести предложение.

Как бы то ни было, Джордж пришел, рассказал о q -серии и представил множество открытых задач. Написание моей диссертации к настоящему времени было почти завершено, так что я мог свободно погрузиться в проблемы Джорджа. Я нашел решения для нескольких из них.

В то время перспективы моей работы не были радужными. Я был на Совместных Математических Совещаниях и вышел только с одной многообещающей зацепкой. Мне показалось, что SUNY Binghamton заинтересовался мной. Прежде чем они приняли какое-либо решение, я получил предложение от Penn State. Как я позже узнал, математический факультет штата Пенсильвания не нанимает никого, кто не имеет сторонника среди своих преподавателей, а влиятельный сторонник, такой как Джордж, имеет большой вес. Мне предложили двухгодичную гостевую должность.

Весна выдалась на редкость урожайной. К июню я доказал один из своих самых значительных результатов — обобщение тождеств Роджерса-Рамануджана, распространяющееся на любой модуль. В 1961 году Бэзил Гордон опубликовал расширение тождеств Роджерса-Рамануджана на любой нечетный модуль (рис. 1). К 1967 году у Джорджа Эндрюса был случай, когда модуль конгруэнтен 2 по модулю 4, а значение r , дающее два исключенных класса остатков, отличных от 0, является нечетным. Он включил случай, когда модуль равен 2 по модулю 4 и 9.0075 r есть даже в его 1976 The Theory of Partitions . Весной 1977 года, готовясь к поступлению в Государственный колледж, я обнаружил и доказал случай произвольного четного модуля (рис. 2).

Рис. 1. Теорема, опубликованная Бэзилом Гордоном в 1961 г.

Рис. 2. Мое обобщение теоремы Гордона, опубликованное в 1979.

Это, в свою очередь, привело к многочисленным обобщениям и расширениям этих тождеств и их аналитических основ, которые я опубликовал в качестве мемуаров AMS в 1980 году. -трековая позиция в Penn State.

Мой прогресс был до крайности необычным. Я прошел путь от докторской степени в Исследовательском университете 2 до постоянной должности, а затем стал профессором в одном из 25 элитных государственных Исследовательских университетов 1. Я понимаю, насколько моя последующая карьера была построена на вмешательстве Дика и Джорджа. Я навсегда у них в долгу.

Этот опыт преподал мне два важных урока при выборе научного руководителя. Во-первых, это должен быть кто-то, с кем вы можете легко установить контакт. Конкретная область, в которой человек хочет работать, имеет гораздо меньшее значение. На самом деле Гроссвальд специально предупредил меня, чтобы я не ожидал, что буду продолжать работать в области, в которой получил докторскую степень. Докторская степень — это сигнал о том, что человек способен внести существенный, оригинальный вклад в математику в широком смысле, не более того. Во-вторых, чрезвычайно важна репутация консультанта докторской диссертации и то, насколько он или она подключены к сети исследователей. Это никогда не должно перевешивать первое соображение. Из многих уважаемых математиков получаются паршивые советники. Но это важное соображение для начала успешной карьеры.

Первый шаг в установлении соответствия между двумя типами разбиений состоит в том, чтобы отметить, что целые числа, конгруэнтные +1 или –1 по модулю 6, являются просто нечетными целыми числами, которые не делятся на 3. Эйлер использовал производящие функции, чтобы установить, что количество разбиений n на нечетные целые числа равно количеству разбиений на разные целые числа. Харди и Райт дали хорошее комбинаторное доказательство. Любое доказательство показывает, что исключение кратных 3 среди нечетных целых чисел означает исключение кратных 3 среди различных целых чисел. Поскольку оно чисто комбинаторное, я приведу доказательство Харди и Райта. 90) умножить на нечетное целое число (которое может быть 1), которое я буду называть нечетным корнем . Мы берем различные целые числа и группируем те, которые имеют один и тот же нечетный корень. Сумма соответствующих степеней двойки дает уникальное целое число, которое будет обозначать, сколько раз это нечетное число появляется при разбиении на нечетные целые числа. Например, разбиение на отдельные целые числа 1 + 4 + 5 + 6 + 8 + 20 группируется как (1 + 4 + 8)*1 + (2)*3 + (1 + 4)*5, что дает тринадцать единиц, две тройки и пять пятерок. Это однозначно обратимо. Если среди различных целых чисел нет кратных 3, среди нечетных чисел не будет кратных 3, и наоборот.

Следующим произведением был мой вклад. Учитывая разбиение на различные целые числа, не кратные 3, мы находим самую большую пару, которая отличается менее чем на 3, и складываем их вместе, затем продолжаем движение вниз среди оставшихся целых чисел, пока не найдем следующую самую большую пару с разницей меньше 3, и снова добавить их вместе. Продолжайте до тех пор, пока все числа, не делящиеся на 3, будут отличаться как минимум на 3. В каждой паре обязательно одно из чисел сравнимо с +1, а другое –1 по модулю 3, поэтому каждая сумма делится на 3. Рассмотрим следующий пример. ,

1+2+4+7+8+14 -> 1 + 6 + 15 + 14. Отнимаем 3 от второго числа, 6 от третьего и вообще 3( k –1) от к -й. Размещаем оставшиеся целые числа в порядке возрастания, затем прибавляем обратно 3 ко второму, 6 к третьему и так далее,

1 + 6 + 15 + 14 => 1 + 3 + 9 + 5 => 1 + 3 + 5 + 9 => 1 + 6 + 11 + 18.

Все эти числа будут отличаться не менее чем на 3, а кратные 3 должны отличаться не менее чем на 6, поскольку на промежуточном этапе кратные 3 различны. Что может быть не сразу очевидно, так это то, что эта процедура однозначно обратима.

К сожалению, проверка, которую мне пришлось использовать, показанная на рисунках 3, 4 и 5, не так проста, как хотелось бы. Заметьте, что сама теорема и мое доказательство носят более общий характер.

Для 0 < r < m /2 число разбиений n на отдельные части, конгруэнтные + r или – r по модулю m , равно количеству разбиений 9075 m n на части, равные 0, + r , или – r по модулю м , отличающиеся не менее чем на м , с частями, кратными м , отличающимися не менее чем на 2 м . То же самое соответствие работает и для этого более общего случая. Вы можете найти полное утверждение и доказательство в моей статье «Комбинаторное доказательство теоремы Шура 1926 года о разделении», которая была опубликована в Proceedings of the American Mathematical Society , vol. 79, 1980, 338–340.

Должен добавить, что после публикации я понял, что статья мне не понравилась в том виде, в котором она написана. В нем отсутствуют примеры или какое-либо ощущение простоты идеи. Именно это подчеркивал Алдер в своем выступлении, игнорируя уникальную обратимость и просто утверждая ее истинность. Конечно, это была публичная презентация, а не строгое доказательство. Хотя опубликованное исследование должно быть логически завершенным, оно также должно отражать дух доказательства. Мне не удалось сделать это в этой статье, но я научился этому неправильному представлению. В каком-то смысле эта колонка — моя попытка исправить эту ошибку

Рисунки 3–5. Завершение доказательства теоремы Шура.

 

Каталожные номера

Ольха, H.L . (1956). № исследовательской задачи. 4, Бюлл. амер. Мат. соц.   62 , 76

Алфес, К., Джеймсон, М. и Лемке Оливер, Р.Дж., (2011), Доказательство гипотезы Альдера-Эндрюса, Проц. АМС , 139 , 63–78.

Эндрюс, Г.Э. (1967). Некоторые новые теоремы о разбиении. J. Комбинаторная теория , 2 , 431–436.

Эндрюс, Г.Э. (1971). О проблеме разбиения Г. Л. Альдера. Pacific J. Math ., 36 , 279–284.

Эндрюс, Г.Э. (1976). Теория разделов . Чтение, Массачусетс: Аддисон-Уэсли.

Брессо, Д. (1979). Обобщение тождеств Роджерса-Рамануджана для всех модулей. J. Комбинаторная теория, серия A . 27 , 64–68.

Брессо, Д. (1980). Комбинаторное доказательство теоремы Шура 1926 года о разделении, Proc. АМС , 79 , 338–340.

Брессо, Д. (1980). Аналитические и комбинаторные обобщения тождеств Роджерса-Рамануджана.