Схема подключения дифавтомата
Если вы решили защитить своих близких и имущество с помощью дифавтомата (АВДТ), то правильно делаете, но только подключите его правильно. Сначала изучите схему подключения автоматического выключателя дифференциального тока и только потом занимайтесь его монтажом. Хотя тут ничего сложного нет, но если все равно сомневаетесь как подключить дифавтомат, то ниже я подробно рассказал как это сделать…
Подключение дифавтомата практически похоже на подключение УЗО, но только здесь в схеме отсутствует дополнительный автоматический выключатель. На что тут нужно обратить особое внимание при подключении дифавтомата:
- Подключение проводов. Приходящий провод всегда подключается только на верхние контакты, а отходящий всегда на нижние. Не меняйте их местами. От этого может сгореть АВДТ и тогда побежите в магазин за новым. Если вдруг у вас не хватает длины проводов до нужных контактов, то замените провод.
- Соблюдение полярности
- Следите за нулевыми проводниками. Как мы привыкли “нуль” должен быть везде общим и должен объединять все нулевые проводники. А вот использование дифавтомата немного нарушает это правило. Запомните, что объединение нулей после АВДТ запрещено. После дифавтомата фаза и нуль ушли только в контролируемую данным АВДТ цепь и на всем ее протяжении ни с чем больше не объединяются.

Схема подключения дифавтомата
Теперь ниже давайте рассмотрим несколько схем подключения дифавтомата, которые могут встретиться в обычных квартирах.
В варианте предложенным ниже предлагается установка общего входного автоматического выключателя дифференциального тока, который будет защищать всю квартиру. Рекомендованные параметры АВДТ приведены на схеме, но учтите что у каждого разная нагрузка и нужно ее считать индивидуально.
Плюсы такой схемы:
- дешевизна, так как необходим только один АВДТ;
- необходимо немного места в распределительном щитке.
Минусы:
- при срабатывании дифавтомата обесточивается вся квартира;
- затруднен поиск неисправности (В какой линии произошла утечка? А может было короткое замыкание?)
Следующая схема подключения дифавтомата состоит из общего входного АВДТ и дифавтоматов в каждой отходящей линии. Это самый безопасный и надежный вариант схемы распределительного щитка. Тут входной АВДТ контролирует всю сеть, а групповые дифавтоматы контролируют каждый свою цепь.
В данном варианте необходимо соблюсти селективность в выборе автоматических выключателей дифференциального тока. Групповые выбираем с током утечки 30мА, а входное с током утечки 100-300мА. Это нужно чтобы при неисправности к какой-либо цепи не сработали сразу групповой и входной дифавтоматы. Также селективность может быть достигнута с помощью применения АВДТ типа “S” (селективного). Оно имеет задержку в времени срабатывании, что дает возможность сработать только одному групповому АВДТ.
Плюсы такой схемы:
- надежность и безопасность;
- при аварии обесточивается только неисправная линия, что облегчает поиск места неисправности.
Минусы:
- дороговизна, так как дифавтоматы стоят недешево;
- необходимо много место в распределительном щитке, чтобы все это разместить;
- сложность схемы (может это и не минус).

Последняя предлагаемая схема подключения дифавтомата является почти аналогичной предыдущей схемы, но только без применения общего входного АВДТ. Многие говорят, что зачем тратить лишние средства на входной дифавтомат, так как каждая цепь уже контролируется автоматическим выключателем дифференциального тока. Плюсы и минусы такой схемы такие же как и в предыдущем варианте.
Если у Вас остались вопросы, то задавайте их в комментариях. Будем вместе разбираться что к чему.
Вот несколько фотографий, где показано наглядно подключение дифавтоматов. Это моя работа по сборке и подключению электрощитов. Для заказа разработки схемы распределительного щита и его сборки пишите запрос в любой форме на адрес Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. . Готовые электрощиты отправляю в любую точку России через транспортные компании. При заказе сборки схему разрабатываю бесплатно.
Специально для Елены ответ на комментарий №2. Схема подключения дифавтомата как делать НЕЛЬЗЯ.
Улыбнемся:
Тост:
Висел на столбе электромонтер, сжимал зубами два куска провода. Бежала мимо лиса:
– Монтер-монтер, а что это ты на проводах раскачиваешься, хоть бы лестницу поставил!
Молчит монтер, сжимает провода пуще прежнего. А лиса не унимается:
– Монтер, ты бы хоть паяльник взял, разве можно зубами?
Молчит монтер. А лиса снова:
– Монтер, ты электричество-то выключи, ведь тебя сейчас током долбанет!
– А ну вали отсюда, дура рыжая, ты еще будешь меня учить работать!
А как разжал зубы – вниз брякнулся и ногу вывихнул. А провода разомкнулись, и во всем городе свет погас.
Так выпьем за то, чтобы не обращать внимания на советы дилетантов.
устройство и принцип работы, монтаж, схемы и способы подключения в распределительном щите
Электричество — это, безусловно, благо.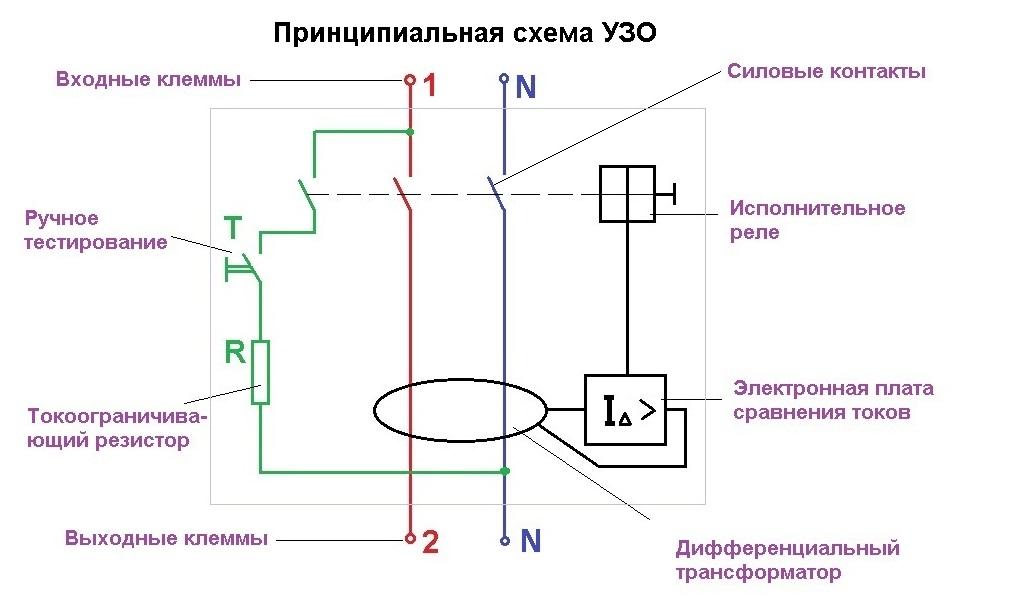 Однако, обращаться с ним нужно осторожно, ведь из-за короткого замыкания или перепадов напряжения в электросети могут пострадать бытовые приборы. А для человека, случайно соприкоснувшегося с электропроводкой под напряжением, может все кончится летальным исходом. Защитить имущество и окружающих можно с помощью специального прибора, о нем и пойдет речь ниже.
Однако, обращаться с ним нужно осторожно, ведь из-за короткого замыкания или перепадов напряжения в электросети могут пострадать бытовые приборы. А для человека, случайно соприкоснувшегося с электропроводкой под напряжением, может все кончится летальным исходом. Защитить имущество и окружающих можно с помощью специального прибора, о нем и пойдет речь ниже.
Дифференциальный автомат: общие сведения
Дифференциальный автомат (дифавтомат) — является электромеханическим устройством, которое имеет два основных предназначения:
- защитить электрическую цепь от утечки токов на землю;
- защитить цепь от перегрузки в сети и короткого замыкания.
Дифференциальный автомат соединяет в себе функции УЗО и автоматического выключателя. Как УЗО, дифавтомат полностью защищает человеческий организм от поражения электричеством при соприкосновении с токонесущей частью электрооборудования.
Кроме этого, дифференциальный автомат отлично защищает сеть от короткого замыкания и перегрузок, то есть ведет себя, как автоматический выключатель.
Конструкция дифавтомата отличается от аналогичных ему устройств. В малом с виду корпусе удачно сочетаются и действуют два защитных прибора: УЗО и автоматический выключатель. Благодаря этому, дифференциальный автомат может быстро произвести защитное отключение. Соответственно это может произойти в случае утечки тока, перегрузки сети или короткого замыкания.
Принципы работы дифавтомата
Встроенный в дифавтомат автоматический выключатель обеспечивает защиту от перегрузок в сети и короткого замыкания. В этот защитный модуль входит устройство расцепления контактов. Оно сработает если в электрической сети возникнет перегрузка или короткое замыкание. Также автомат имеет рейку сброса. Она приводится в действие благодаря внешнему механическому воздействию.Для защиты человека от воздействия электричества в дифавтомате встроен модуль дифференциальной защиты, в который входит дифференциальный трансформатор. Это устройство проводит постоянное сравнение текущих через него токов на входе и на выходе. Если обнаружится разница, которая несет угрозу, защитный модуль с помощью усилителя и электромагнитной катушки преобразует электрический ток в механическое действие, что и обесточит цепь.
Это устройство проводит постоянное сравнение текущих через него токов на входе и на выходе. Если обнаружится разница, которая несет угрозу, защитный модуль с помощью усилителя и электромагнитной катушки преобразует электрический ток в механическое действие, что и обесточит цепь.
Монтаж и схема подключения дифференциального автомата
При подключении дифавтомата нужно руководствоваться следующим правилом: в дифференциальный автомат подсоединяются ноль и фаза той цепи, которую будет защищать дифавтомат. Ни в коем случае нельзя объединять нулевой провод, приходящий с автомата с другим нулевым проводом. Это приведет к отключению дифавтомата.
Монтаж дифавтомата: схема подключения №1
Первая схема подключения защищает все электрические группы при помощи одного дифференциального автомата. Устройство устанавливают на входе цепи.
Во второй схеме дифавтомат, подключенный в цепь, защищает определенную электрическую группу. Этот вариант применяется для разработки надежной электробезопасности в помещении, где находится электрическая группа.
Если дифавтомат подключается по первому варианту, то к верхним клеммам прибора подводятся провода с питающим напряжением, а к нижним — подключают нагрузку от каждой группы в отдельности. При этом группы предварительно разделены электрическими выключателями.
Главный минус такого варианта подключения является то, что в случае аварийного срабатывания автомата полностью отключатся все электрические группы.
Чтобы избежать ложного срабатывания вводного дифавтомата, рекомендуется применять автомат с током утечки 30 мА.
Монтаж дифференциального автомата: схема подключения №2
Этот вариант защиты электрической сети дифавтоматом считается наиболее надежной и удобной. Часто эта схема применяется в помещениях с повышенными требованиями по электробезопасности или во влажных помещениях — кухня или ванная комната. Особенностью второй схемы подключения дифавтомата является то, что аварийное отключение одного дифавтомата не повлечет за собой отключение остальных. Безусловно, это положительный момент такой схемы подключения дифференциального автомата для защиты необходимых групповых линий. Впрочем, эта схема стоит дороже по сравнению с первой.
Часто эта схема применяется в помещениях с повышенными требованиями по электробезопасности или во влажных помещениях — кухня или ванная комната. Особенностью второй схемы подключения дифавтомата является то, что аварийное отключение одного дифавтомата не повлечет за собой отключение остальных. Безусловно, это положительный момент такой схемы подключения дифференциального автомата для защиты необходимых групповых линий. Впрочем, эта схема стоит дороже по сравнению с первой.
Монтаж дифавтомата: подключение по селективной схеме
Разобраться, чем отличается селективная схема подключения от неселективной, можно на примере двух схем, приведенных ниже.
Для простоты понимания опишем эти схемы, как схемы условной электрической разводки на лестничной площадке дома. Вводный дифавтомат размещается в распределительном щите на площадке, а остальные дифавтоматы пусть будут установлены в трех квартирах.
Схема с селективным подключением дифавтомата.
Принцип работы такой: если из-за повреждения происходит аварийное отключение автомата в одной из квартир, то автоматы в остальных квартирах и дифавтомат в распределительном щите будут продолжать работать. В селективной схеме дифавтомат имеет обозначение «S» — селективный.
Схема без селективного подключения дифавтомата.
При срабатывании на отключение автомата в квартире, происходит отключение дифавтомата и в распределительном щите. Кроме поврежденной линии обесточиваются и две рабочие. Это происходит потому что дифавтомат в распределительном щите рассчитан на ток утечки 100 мА, а отводные автоматы рассчитанны на 30 мА. Очень важно правильно подобрать автомат по току утечки.
В зависимости от вида дифавтомата, схема подключения будет либо селективной либо неселективной.
youtube.com/embed/m6q9aGaAbwg”/>
Правила монтажа дифавтомата в распределительном щите
Подключая дифавтомат в распределительном щите, нужно следовать определенным правилам.
- Подсоединять фазу следует на вход дифавтомата, то есть туда, где на верхней части устройства имеются обозначения «1» или «L».
- Рядом с ними будет стоять буква «N» — это вход нуля на дифавтомат.
- Выход фазы с устройства находится в нижней части и обозначен «2» или «L».
- Выход нуля с прибора тут же и имеет обозначение «N».
Дифавтомат подключается, следуя приложенной к прибору инструкции.
Мастер, производящий подключение, должен четко осознавать какой из проводов и куда нужно подключать. Определить фазу можно с помощью отвертки-индикатора.
Дифавтоматы подключаются как к однофазной сети, так и к трехфазной сети переменного тока.
Подключение дифференциального автомата проводится с соблюдением всех мер электробезопасности.
Если недостаточно средств или не хватает места в распределительном щите, то стоит выбрать схему №1. Но нужно учесть, что если сработает водный дифавтомат — вся квартира будет обесточена. Также в этой схеме очень сложно искать неисправности.
Если есть время и желание повозится с более сложной схемой, хватает финансов на покупку дифавтоматов, а также имеется много места в распределительном щите, то можно смело выбирать схему №2. Она обеспечит надежность и безопасность. Ведь в случае аварии отключится лишь одна линия, а, значит, искать неисправность в такой схеме будет гораздо легче.
Что касается селективной и неселективной схем, то они, независимо от выбора дифавтомата, считаются очень надежными и вполне могут защитить людей, бытовые приборы и сеть.
Схема подключения дифференциального автомата. Подключение дифференциального автомата
Дифференциальный автомат или автоматический выключатель дифференциального тока – электромеханическое устройство, предназначенное для защиты электрической цепи от утечки токов на землю и защиты цепи от перегрузок и коротких замыканий.
Иными словами, дифференциальный автомат одновременно выполняет функции УЗО и автоматического выключателя.
Основным предназначением дифавтомата, является полная защита человека от поражения электричеством при его контакте с токоведущими частями электрооборудования. В этом и проявляется его функция как УЗО.
Помимо этого, данное устройство не менее эффективно защищает электрическую сеть и электрооборудование от перегрузки и короткого замыкания, выполняя функцию автоматического выключателя.
Основная отличительная особенность дифференциального автомата, от аналогичных ему приборов заключается в его конструкции. В не большом по размерам корпусе удачно объединены и функционируют два отдельных защитных устройства: УЗО и автоматический выключатель.
Поэтому защитное отключение происходит при любых трех нарушениях в работе электрической сети:
- – утечка тока;
- – перегрузка;
- – короткое замыкание.
Принцип работы дифференциального автомата
Защиту электрической цепи от перегрузки и короткого замыкания осуществляет встроенный модуль защиты – автоматический выключатель. В него входит механизм независимого расцепления контактов, который срабатывает при возникновении в защищенной электрической цепи короткого замыкания и перегрузок. Кроме этого защитный модуль снабжен рейкой сброса приводящейся в действие внешним механическим воздействием.
Защиту человека от поражения электрическим током данное устройство осуществляет при помощи модуля дифференциальной защиты. Он оснащен дифференциальным трансформатором, который постоянно сравнивает проходящий через него ток на входе и на выходе.
В случае обнаружения разницы, представляющей угрозу для жизни, модуль при помощи встроенного электрического усилителя и катушки электромагнитного сброса преобразовывает ток в механическое воздействие, которое и обесточивает защищенную цепь.
Схема подключения дифференциального автомата
Схема подключения дифференциального автомата практически не отличается от схемы подключения УЗО. Поэтому при его подключении необходимо соблюдать те же самые правила: к дифференциальному автомату, как и к УЗО, должны подключаться фаза и ноль только той цепи, которые он будет защищать.
Поэтому при его подключении необходимо соблюдать те же самые правила: к дифференциальному автомату, как и к УЗО, должны подключаться фаза и ноль только той цепи, которые он будет защищать.
| То есть, нельзя нулевой провод который вышел с автомата объединять с другими нулевыми проводами. В этом случае дифавтомат будет отключаться, потому что по этим проводам будут протекать разные токи. |
Первая схема подразумевает защиту всех электрических групп одним дифференциальным автоматом, который устанавливается на вводе (вводной дифавтомат), а вторая схема используется при защите автоматом определенной электрической группы, путем включения его в ее цепь. Обычно этот способ применяют для создания более надежной электробезопасности помещений, в которых расположена эта группа.
При подключении устройства первым способом провода с питающим напряжением подключают к верхним клеммам, а к нижним подают нагрузку от каждой электрической группы, предварительно разделенные автоматическими выключателями.
Существенным недостатком применения данной схемы является полное отключение всех групп при аварийном срабатывании автомата в случаи возникновения неполадок в любой защищенной электрической группе.
Для предотвращения ложных срабатываний вводного дифавтомата, установленного в жилых помещениях (особенно со старой проводкой) на утечку тока, рекомендуется применять дифференциальные автоматы, настроенных на срабатывание с током утечки 30 мА.
Наиболее надежным и удобным способом защиты электрической сети при аварийных ситуациях дифференциальным автоматом, считается подключение дифавтомата по второй схеме.
Чаще всего он применяется для защиты электрических групп размещенных в помещениях с повышенной влажностью – ванных комнатах, кухнях или в помещениях к которым предъявляются повышенные требования по электробезопасности – например, детская комната.
Бесспорно, что защита, каждой электрической группы отдельным автоматом дает более эффективный результат.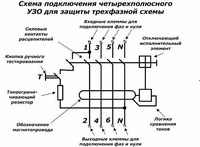 Причем это касается не, только электробезопасности, но и практичности, ведь если по какой либо причине сработает один дифавтомат, то это не повлечет за собой полное обесточивание электросети. Что, безусловно, можно отнести еще к одному положительному отличию применения схемы подключения нескольких устройств, для защиты нужных групповых линий.
Причем это касается не, только электробезопасности, но и практичности, ведь если по какой либо причине сработает один дифавтомат, то это не повлечет за собой полное обесточивание электросети. Что, безусловно, можно отнести еще к одному положительному отличию применения схемы подключения нескольких устройств, для защиты нужных групповых линий.
Применение данного метода будет гарантией надежного и бесперебойного электроснабжения. Однако, применение данного метода подключения защитных устройств, по понятной причине обойдется значительно дороже, чем защита одним аппаратом всей электросети.
Что такое селективная схема подключения дифференциальных автоматов
Разберемся в чем разница между селективной и не селективной схемой подключения. Имеется два рисунка: одна площадка и три квартиры на первом рисунке, на втором рисунке вторая площадка тоже с тремя квартирами.
Что произойдет если вдруг в какой то из квартир возникнет утечка. В правильной схеме (селективной) отключится только поврежденная квартира, автомат на площадке останется включенным и остальные, (неповрежденные) квартиры будут получать питание.
Вторая схема собрана без селективных дифференциальных автоматических выключателей, поэтому здесь при возникновении повреждения в одной из квартир отключится автомат этой квартиры плюс еще и автомат на площадке.
Таким образом обесточатся не только поврежденная линия но и две неповрежденных. С чем это связано? Ведь диффавтомат на площадке 2 рассчитан на ток утечки 100 мА, а отходящие автоматы рассчитаны на ток утечки 30 мА.
Подбор автоматов по току утечки конечно важно учитывать при подключениях но это не является основанием для селективной работы схемы.
| Селективной является схема в которой диффавтомат имеет обозначение «S» – селективный. То есть диффавтомат на площадке не селективный. |
Правила монтажа
Большой популярностью у потребителей пользуются дифференциальные автоматы с номинальным током утечки до 30 мА. Дифференциальные автоматы успешно используются как в однофазных, так и в трехфазных электрических сетях переменного тока.
Дифференциальные автоматы успешно используются как в однофазных, так и в трехфазных электрических сетях переменного тока.
Прежде чем установить их на необходимый участок цепи, надо правильно определить его функциональные возможности. При выборе автоматов, что бы избежать ненужных срабатываний от перегрузок, необходимо учитывать количество потребителей подключенных к данной цепи.
Похожие материалы на сайте:
Понравилась статья – поделись с друзьями!
схема подключения и особенности, видео
Дифференциальный автомат – это устройство, состоящее из двух функциональных узлов, и предназначенное для защиты электросети. Первый узел – автоматический выключатель, а второй – модуль дифзащиты. Основное назначение дифференциального автомата – защита человека от поражения электротоком. Защита обеспечивается быстрым срабатыванием автомата, который размыкает электрическую цепь (для устройства с пределом срабатывания 20 мА, скорость срабатывания — 0,04 секунды).
Разница дифавтомата и УЗО
Многие считают, что существенной разницы между устройством защитного отключения и дифатоматом нет. Они похожи внешне и имеют практически аналогичный принцип действия. Но все же характерные различия между ними есть:
1.УЗО – это коммутационный аппарат, который используется для защиты человека от прямого или косвенного поражения электрического тока. Также он осуществляет контроль за состоянием проводки и отключает подачу питания при наличии ее повреждений. Таким образом, УЗО не защищает электрическую сеть от коротких замыканий – для этого требуется автоматический выключатель.
2. Дифференциальный автомат – это коммутационное устройство, который является, и УЗО, и автоматическим выключателем. То есть его функционал гораздо шире.
Внешние отличия этих устройств:
- название – указывается сбоку или на лицевой стороне корпуса;
- маркировка – если на корпусе указывается только значения номинального тока, при этом буквенные обозначения перед числом отсутствуют, то перед вами УЗО; если перед маркировкой имеется буква B, Cили D, то это – дифавтомат.

Более старые модели имеют еще и различие в габаритах. А вот современные устройства никаких существенных отличий по этому показателю не имеют.
Схема подключения дифавтоматаПо способу подключения дифференциальные автоматы делятся на два типа:
- вводные;
- отдельные.
В обоих вариантах устройство подключается к нулю и фазе той цепи, которую оно будет защищать. Рассмотри оба варианты более подробно.
Подключение вводного дифавтоматаЭта схема подразумевает использование одно дифференциального устройства на вводе для защиты нескольких групп электрических потребителей. Основной недостаток такого метода – при возникновении аварийной ситуации на одной группе, автомат отключает электрическую сеть для всех потребителей.
Подключение отдельного дифавтоматаОтдельный дифавтомат применяется для защиты одной электрической группы. Как правило, такая схема используется в помещения, где предъявляются высокие требования к электрической безопасности. Эта схема более надежная, так как в аварийной ситуации отключается только поврежденная сеть, а остальные группы продолжают работать в штатном порядке.
Правила подключения дифференциальных автоматов к сети
Все устройства поставляются с подробной инструкцией по установке, но несмотря на это, многие испытывают определенные сложности при их монтаже.
Во всех случаях аппараты подключаются следующим образом:
1.Вход дифференциального автомата обозначается цифрой «1», либо буквой латинского алфавита «L». К входу подсоединяется фаза.
2.Рядом с фазой находится вход для нуля. Он обозначается латинской буквой «N».
3.В нижней части корпуса находится выход дифавтомата. Под цифрой «2» или буквой «L» находится фаза.
4.Рядом с выходом фазы находится выход нуля. Он обозначается буквой «N».
Следующим моментом является правильность определения фазы и нуля на проводах. Для этого понадобиться индикаторная отвертка. Провода обычно имеют цветовую маркировку, позволяющую определить принадлежность каждой жилы.
Для этого понадобиться индикаторная отвертка. Провода обычно имеют цветовую маркировку, позволяющую определить принадлежность каждой жилы.
Дифференциальные автоматы используются, как в однофазных, так и трехфазных электрических сетях с переменным током. Подключение этого устройства производится только с заземлением. В сетях, где заземление отсутствует, дифавтомат будет единственным устройством для защиты от утечки тока.
При нарушении изоляции дифавтомат, конечно, не сработает, но если появится утечка, то есть человек возьмется за часть оборудования с фазой, то дифавтомат отключит питание. Это возможно благодаря принципу работы устройства, основанном на разности потенциалов и дифференциальной разбалансировке.
для чего нужен, схема подключения (в том числе в однофазной сети)
Развитие технологии защиты в электрических сетях различного назначения привело к появлению удобного и практичного устройства — дифференциального автоматического выключателя тока. Статус практичного прибора дифавтомат заслуживает благодаря объединению нескольких защитных функций. В отличие от устройств узкого профиля, использующихся для осуществления защиты от конкретных явлений в электрической сети, дифавтоматы обеспечивают комплексную защитную технологию. Принцип действия и условия работы защиты описаны далее.
Для чего нужен дифавтомат в электропроводке
Прежде всего, дифавтомат — это защитное устройство. Как и обычный автоматический выключатель, дифавтомат защищает участок цепи, на котором он установлен, от перегруза и короткого замыкания. При возникновении таких явлений в цепи, дифавтомат отключит участок, находящийся под его защитой аналогично обычному автоматическому выключателю.
Дополнительно дифавтомат оснащён функцией защиты человека от поражения электрическим током при случайном прикосновении человека к токоведущим частям.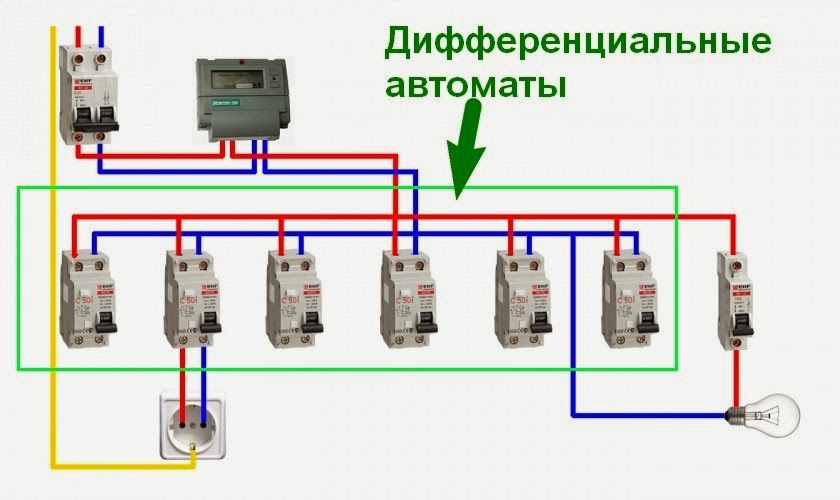 В этом смысле дифавтомат выполняет функцию УЗО.
В этом смысле дифавтомат выполняет функцию УЗО.
Такое сочетание необходимых видов защит делает дифавтомат востребованным в процессе монтажа и эксплуатации электрических сетей различного назначения.
Универсальность этого устройства подтверждается его размерами, которые особо не увеличились при объединении функций двух других устройств. Дифавтомат устанавливается на дин-рейку аналогично другим приборам.
Объединение функций УЗО и автоматического выключателя
Сохранность и работоспособность электрической сети во многом зависит от используемых устройств защиты. Но самой большой ценностью во все времена остаётся человеческая жизнь. Защита людей, обслуживающих и эксплуатирующих электрические сети, всегда должна оставаться в приоритете. В этом смысле дифавтомат является оптимальным решением в оборудовании защищаемой электросети.
При несомненных практических преимуществах, дифавтоматы ещё и несколько экономичнее, чем отдельная установка УЗО и автоматического выключателя.
Об особенностях подключения перекрёстного выключателя можно прочитать в данном материале: https://aqua-rmnt.com/ehlektrosnabzhenie/perekryostnyj-vyklyuchatel-dlya-chego-nuzhen-i-kak-ego-podklyuchit.html
Принцип работы и методы срабатывания
Принцип работы дифавтомата также объединяет принципы работы автоматического выключателя и УЗО. Для защиты от токов короткого замыкания и перегрузки в сети дифавтомат оснащён электромагнитным и тепловым расцепителями, а для защиты от тока утечки — дифференциальным трансформатором и отключающей катушкой.
В случае попадания человека под действие тока на участке цепи, защищаемом дифавтоматом, сработает отключение от появления тока утечки. В дифференциальном трансформаторе нарушиться баланс магнитных потоков и отключающая катушка на это отреагирует мгновенно.
Возникновение тока утечки
В случае же перегруза электрической цепи работу по отключению выполнит тепловой расцепитель, конструктивно и номинально не отличающийся от тепловых расцепителей обычных автоматических выключателей. А при возникновении в цепи тока короткого замыкания, свою работу выполнит магнитный расцепитель, который также не отличается от магнитных расцепителей автоматических выключателей.
А при возникновении в цепи тока короткого замыкания, свою работу выполнит магнитный расцепитель, который также не отличается от магнитных расцепителей автоматических выключателей.
Расположение магнитного и теплового расцепителей
В зависимости от схемы монтажа дифавтоматов, различают селективный и неселективный методы срабатывания.
Селективность — это избирательность в процессе защиты. При возникновении аварии селективная защита должна отключить минимальное количество потребителей, находящихся на защищаемом участке.
В качестве примера: при возникновении неисправности в бытовом электроприборе, предохранитель должен сработать в самом приборе, а не в распределительном щите всего здания.
Селективная схема предусматривает использование дифавтомата с обозначением S на передней панели, что собственно и обозначает «селективный».
Селективная схема монтажа реализовывается за счёт установки одного дифавтомата (селективного) на вводе (центральный распределительный щит, электрощит на лестничной клетке и т. п.) и нескольких неселективных дифавтоматов в отходящей цепи. По одному на каждый участок.
Вводной дифавтомат и три отходящих участка цепи
Такая схема монтажа предпочтительнее из-за того, что при возникновении аварии на любом из трёх защищаемых участков, отключение выполнит неселективный дифавтомат, а основной останется включённым. Такой способ срабатывания обеспечивает существенное снижение риска отключения всех потребителей одновременно.
Неселективная схема монтажа реализована аналогично предыдущей, но с существенным отличием. Вводной дифавтомат не селективного исполнения, а такого же, как и отходящие дифавтоматы. В случае возникновения аварии на любом из участков цепи отключится дифавтомат, защищающий этот участок, а также вводной дифавтомат, что, в свою очередь, приведёт к отключению всех групп потребителей.
Функционально неселективная схема выполняет защиту правильно, но в плане эксплуатации она непрактична.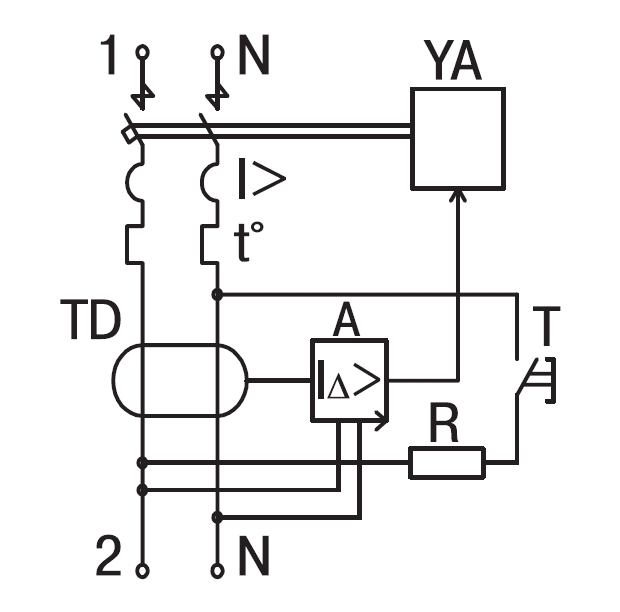
Монтаж селективной схемы защиты более предпочтителен.
Об обозначении розеток и выключателей на строительных чертежах и электрических схемах можно прочитать здесь: https://aqua-rmnt.com/ehlektrosnabzhenie/oboznachenie-rozetok-i-vyklyuchatelej-na-stroitelnyx-chertezhax-i-elektricheskix-sxemax.html
Схема подключения дифференциального автоматического выключателя тока
Схема подключения дифавтомата рассмотрена на примере бытовой электросети 220 В.
Схему можно реализовать по-разному, в зависимости от бюджета и личных предпочтений в формировании защиты домашней электрической сети.
Относительно экономичный вариант предусматривает установку одного дифференциального автомата на вводе в квартиру или дом, а на каждый защищаемый участок установку обычного автоматического выключателя. При такой схеме защита от перегруза и короткого замыкания осуществляется на каждом из участков благодаря работе автоматических выключателей. А защита от тока утечки реализована во всей цепи за счёт дифавтомата на вводе.
Подключение вводного дифавтомата в бытовой сети 220В
Следующий вариант подключения предусматривает установку дифавтоматов на каждый участок цепи. В этом случае нет необходимости устанавливать вводной дифавтомат. Каждый из защищаемых участков обеспечен защитой от перегруза, короткого замыкания и тока утечки. Следует заметить, что такой вариант дороже чем предыдущий. Хотя и более правильный, с точки зрения формирования защиты, в электросети.
Схема без вводного дифавтомата в электросети 220 В
Второй вариант схемы подключения предпочтительнее для помещений с повышенной влажностью. В таких помещениях возрастает риск появления токов утечки на землю из-за влажной среды. Для защиты людей необходимо максимально эффективно сформировать защиту от токов утечки. Установка дифавтоматов на каждую группу электроприборов обеспечит высокую степень защиты.
Как правильно подключить
Схема подключения дифавтоматов в сети 220 В рассмотрена выше.
Схема подключения дифавтоматов в сети 380 В имеет существенные отличия. Прежде всего, для такой схемы нужен четырёхполюсный дифавтомат. Такой дифавтомат предназначен специально для трёхфазной сети, имеет более крупные габариты, но также устанавливается на дин-рейку.
Исполнение для трёхфазной сети
Схема установки такого дифавтомата предусматривает его монтаж после счётчика. Такой тип установки можно реализовать селективным способом, если вводной дифавтомат использовать селективного исполнения.
Установка в сети 380 В
При отсутствии заземляющего проводника в схеме питания помещения (дома), установка дифавтомата является обязательной.
Самым уязвимым местом у лампы накаливания является вольфрамовая спираль, которая чувствительна к резким перепадам напряжения. Для того чтобы сгладить эти каскады используют специальные приспособления. Подробности: https://aqua-rmnt.com/ehlektrosnabzhenie/plavnoe-vklyuchenie-lamp-nakalivaniya-220.html
Защита людей от электрического тока прежде всего.
Схема подключения в такой сети реализовывается следующим образом.
Простейшая схема установки в сети 220 В
При такой схеме сам дифавтомат будет выполнять функцию заземлителя, мгновенно реагируя на появление в сети тока утечки на землю. Это обеспечит защиту людей использующих бытовые электроприборы или просто находящихся в защищаемом помещении.
Независимо от вида электрической сети, в которой монтируется дифавтомат, существует ряд правил, обеспечивающих правильность эксплуатации:
- Питающие провода всегда нужно подводить к устройству сверху, а отходящие вниз. Практически на всех моделях дифавтоматов нанесено обозначение присоединений проводов и положение входа и выхода. При случайном подключении нагрузки не стой стороны, можно вызвать аварию, вызывающую выход из строя дифавтомата. Иногда приходится работать в условиях, требующих установки дифавтомата в перевёрнутом положении.
 На эффективность его работы такое положение не повлияет, главное, не перепутать клеммы подключения.
На эффективность его работы такое положение не повлияет, главное, не перепутать клеммы подключения. - Важно соблюдать правильность подключения фазных и нулевого провода. В стандартной международной маркировке клемма подключения фазного провода имеет обозначение L, а клемма подключения нулевого проводника N. Приходящий проводник имеет обозначение — 1, а отходящий обозначение — 2.
- Для нормальной корректной работы дифавтомата, его нулевой проводник должен быть соединён лишь со своей цепью. Запрещено объединять нули всех групп в общую цепь.
Важно помнить, что неправильное подключение устройства защиты не всегда вызовет его поломку. Неправильное подключение всегда не обеспечит должного уровня защиты и правильности её работы.
Видео: устройство и принцип работы устройства
Обеспечение своего жилого пространства защитой — это всегда актуальный вопрос. А обеспечение защитой близких — ещё более актуальный. Автоматические выключатели дифференциального тока помогают решить одну из наиболее важных задач — задачу безопасного использования электроэнергии. Важно, что решение вопроса построено комплексно. Это позволяет оптимально использовать средства монтажа, пространство и время работы, потраченное на оборудование схемы защиты.
Дмитрий. 29 лет. Образование – инженер-механик. Работаю в горнодобывающей промышленности. Оцените статью: Поделитесь с друзьями!Подключение дифференциального автомата – «Электро Проф»
Для обеспечения защиты электрических сетей от утечек тока, перегрузок и коротких замыканий необходимо устанавливать дифференциальные автоматы. По сути они представляют собой сложное устройство, в котором одновременно реализованы функции УЗО и автоматического выключателя. Поэтому их рекомендуется устанавливать не только в сети промышленного масштаба, а и потребительские. Установка дифавтомата достаточно проста и не потребует использования специнструментов или наличия опыта монтажа электросетей.
По сути они представляют собой сложное устройство, в котором одновременно реализованы функции УЗО и автоматического выключателя. Поэтому их рекомендуется устанавливать не только в сети промышленного масштаба, а и потребительские. Установка дифавтомата достаточно проста и не потребует использования специнструментов или наличия опыта монтажа электросетей.
Особенности подключения
Дифференциальный автомат должен подключаться непосредственно к той сети, которую требуется защитить. То есть даже ноль не должен быть общим с другими сетями, так как в таком случае будет срабатывать защита из-за различия в токах.
Способы подключения к сетям однофазным и трёхфазным с заземлением и без него существенно отличаются, поскольку потребуется использование разных конструкций дифавтоматов: двухполюсной или четырёхполюсной.
Рисунок 1. Внешний вид дифавтомата.
Особое внимание при подключении автоматов следует уделять следующим пунктам:
- Вводные провода подключаются только к верхним контактным клеммам, а выходные – к нижним. Если их перепутать, то в лучшем случае будет постоянно срабатывать защита, а в худшем – выйдет из строя защитное устройство. Поэтому если не хватает провода, то лучше его нарастить с применением специальных колодок либо перевернуть дифавтомат, что делать не желательно, так как можно перепутать включённое и выключенное состояние.
- Обязательно соблюдение полярности подключения, то есть ноль и фаза должны соединяться с соответствующими клеммами. Фаза обозначается буквой «L», а нуль – «N». Цифровое обозначение «1» говорит о том, что клеммы вводные, а «2» – выходные. Неправильная полярность может стать причиной несрабатывания защиты от перегрузок и коротких замыканий.
- Соединение нулевых кабелей после автомата запрещено.
Селективная и неселективная схемы подключения
Схема подключения дифавтомата может выполняться по двум принципам: селективному и неселективному. Они позволяют реализовать различную функциональность подключённых сетей и поэтому применяются там, где наиболее целесообразно реализовать именно такую схему. Селективная предназначена для защиты определённой группы подключённых нагрузок, а неселективная – для защиты всех подгрупп сетей. Другими словами, при селективной схеме в случае возникновения нестандартных ситуаций будет отключена только подсеть, где возникли проблемы, а основная электросеть будет запитана. В неселективной при нештатных режимах будут обесточены все подсети.
Они позволяют реализовать различную функциональность подключённых сетей и поэтому применяются там, где наиболее целесообразно реализовать именно такую схему. Селективная предназначена для защиты определённой группы подключённых нагрузок, а неселективная – для защиты всех подгрупп сетей. Другими словами, при селективной схеме в случае возникновения нестандартных ситуаций будет отключена только подсеть, где возникли проблемы, а основная электросеть будет запитана. В неселективной при нештатных режимах будут обесточены все подсети.
Рисунок 2. Подключение по селективной схеме.
В селективной схеме подключение дифференциального автомата, от которого планируется выполнять ответвления на подсети, подбирается по суммарным размерам токов утечки всех подсоединяемых автоматов. То есть при соединении трёх подсетей с дифавтоматами по 30 мА основной автомат, от которого проводится разветвление, должен быть рассчитан на токи утечки не менее 100 мА. Однако это вовсе не значит, что отключение будет производиться селективно, так как дополнительным условием полной реализации схемы является применение специальных автоматов с маркировкой «S». Их особенностью является задержка в срабатывании, по сравнению с обычными, что собственно и предотвращает моментальное отключение всех подсетей. Для неселективной схемы применяют обычные дифавтоматы.
Варианты подключения дифавтоматов к счётчикам
Подключение дифавтомата может быть выполнено по следующим схемам:
1) Установка одного автомата на вводе в объект. Позволяет обеспечить надёжную базовую защиту всей сети при минимальных финансовых затратах. Но при этом станет возможным подключение потребителей с примерно одинаковой нагрузкой. Недостатком такой защиты является сложность поиска проблем утечек тока или коротких замыканий.
Рисунок 3. Подключение по схеме 1.
2) Общий автомат на вводе кабеля на объект с подразделением на несколько вспомогательных линий с отдельными дифавтоматами, то есть селективная защита. В таком случае обеспечивается двойной контроль за безопасностью сети. При этом схема существенно усложняется и становится в несколько раз дороже обычной. Зато при её правильной реализации повышается надёжность и устойчивость к нестандартным ситуациям.
В таком случае обеспечивается двойной контроль за безопасностью сети. При этом схема существенно усложняется и становится в несколько раз дороже обычной. Зато при её правильной реализации повышается надёжность и устойчивость к нестандартным ситуациям.
Рисунок 4. Подключение по схеме 2.
3) Использование параллельного подключения дифавтоматов, отвечающих за защиту отдельных подсетей. В отличие от предыдущего варианта, стоимость оборудования становится меньшей, а все преимущества сохраняются.
Рисунок 5. Подключение по схеме 3.
Рисунок 6. Подключение дифавтоматов к счётчику с заземлением.
Рисунок 7. Подключение к счётчику дифавтоматов по двухпроводной схеме.
Основные ошибки подключения
- Вводные кабели подключены к нижней части из-за невнимательности или незнания схемы и принципа работы автомата. Особенно если учесть, что принципиальная схема указывается на лицевой части корпуса защитного устройства.
- Соединение нулевого провода с нулями других подсетей. Это вызовет разницу в проходящих токах и срабатывание защиты.
- Ошибочное соединение нуля с заземлением. Часто такая схема реализуется при двухпроводной схеме подключения.
- Прямое подключение нейтрали к потребителям, минуя защитное устройство. Это также приведёт к срабатыванию защиты.
- При подключении нескольких дифавтоматов выполнено неправильное соединение фазы и нуля между ними. Это вызовет срабатывание автоматов по отдельности либо сразу всех одновременно.
Подключение дифавтомата своими руками
Проводка должна быть обеспечена защитой от ситуаций, связанных с перегрузками и утечками тока. При этом прибегают к помощи защитного автомата и УЗО. Данную задачу можно решить, если использовать дифференциальный защитный автомат. Он как бы объединяет два прибора в один. Они даже расположены в одном корпусе. Чтобы прибор функционировал полноценно, его следует правильно подключить.
Условия подбора дифавтомата
Немаловажным моментом является экономическая сторона вопроса. Купить один прибор обойдется дешевле, чем приобретать два устройства. Наконец, потребуется лишь определение номинала автоматы защиты. УЗО встраивается по умолчанию в соответствии с необходимыми характеристиками.
К сожалению, не обошлось и без недостатков. Если из строя выйдет лишь какая-то часть прибора, то замене будет подлежать автомат полностью. Понятно, что это сопряжено с дополнительными расходами.
Далеко не все подобные автоматы снабжаются флажком, с помощью которого определяется причина срабатывания прибора, выяснение которой принципиально важно.
Читайте также статью ⇒ Как отличить узо от дифавтомата.
Характеристика и выбор дифференциального автомата
Поскольку прибор состоит из двух устройств, требуется вести учет характеристик каждого из них.
На схемах дифавтоматы обозначаются следующим образом:
Примеры обозначения дифференциальных автоматов, включенных в состав различных схем подключенияПри выборе подходящей модели следует учитывать следующие характеристики:
- Номинальный ток.
Под ним следует понимать величину максимального тока, которую в течение определенного времени выдерживает автомат, не теряя при этом своей работоспособности. Эта величина указана на панели корпуса. Она носит стандартный характер и находится в диапазоне от 6 до 63 А.
Аппараты малого номинала (10-16 А) устанавливают на осветительных линиях. Приборы со средним номиналом связаны с серьезным потребителем и группами розеток. Использование мощных устройств (40 А и выше) применяются на линиях ввода.
Совет №1: Подбор прибора следует осуществлять в соответствии с сечением кабеля.
- Время и электромагнитный расцепитель.
Обозначение ведется латинскими буквами B, C, D. Определяет величину перегрузки, при которой отключится автомат.
На корпусе приборов указываются их основные технические характеристики и параметры работы- Категорийность, обозначаемая буквами, имеет следующую градацию:
- В – превышение тока в 3-5 раз;
- С – номинал превышен в 5-10 раз;
- D – превышение составляет 10-20 раз.

- Величина номинального напряжения и частоты сети
Имеется ввиду специфика сети, для которой предназначается конкретный аппарат, проще говоря, 220 либо 380 В, частотой 50 Гц. Иных вариантов в розничной продаже просто не бывает:
Устройство может иметь двойную маркировку — 230/400 V. Это является свидетельством того, что он применяется, как на сети 220, так и 380 В. Если сеть трехфазная, то установка подобных устройств имеет отношение к розеточным группам. При одной фазе они связаны с отдельными потребителями.
Вводные дифавтоматы в трехфазных сетях должны иметь четыре вывода. По причине своих приличных габаритов спутать их с чем-то другим весьма проблематично.
- Номинальный отключающий дифференциальный ток
Этот показатель связан с чувствительностью прибора по отношению к возникающим утечкам. Он определяет условия срабатывания защиты.
В бытовом плане проводят использование лишь двух номиналов:
- линия с одним мощным устройством;
- сочетание двух опасных факторов, связанных с электроэнергией и водой (посудомоечная машина).
Если речь идет о группе розеток и наружном освещении, то устанавливают дифавтоматы на 30 А. Местом их расположения является линия освещения. Они не монтируются внутри дома из соображений экономии.
- Класс
Этот показатель характеризует тип тока утечки, от которого защищает устройство. Классность защиты определяется типом нагрузки. Техника, имеющая микропроцессоры подпадает под класс А. Линии, идущие на освещение или питание обычных устройств, имеют классность АС. Для частных домов и квартир установка устройств классности В проводится довольно редко, поскольку отсутствует потребность в «отлавливании» всех типов утечек тока.
Класыс S и G используются в многоуровневых схемах защиты. Их устанавливают на входах, если далее схема предполагает наличие других дифференциальных устройств.
Если сработает один из расположенных ниже по схеме приборов, входное устройство будет оставаться в работе.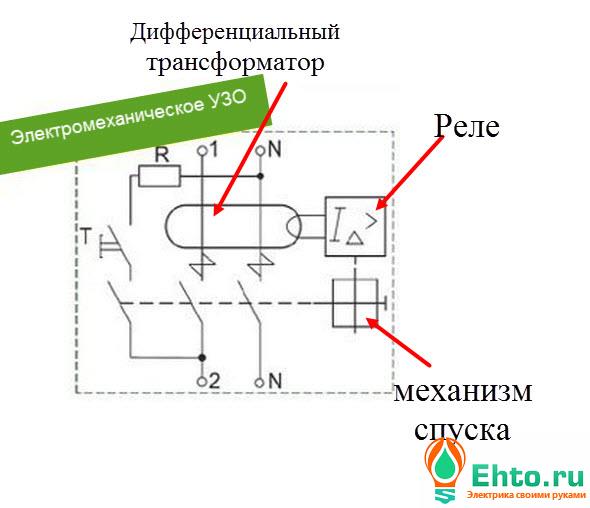
- Величина номинальной отключающей способности.
Если возникнет короткое замыкание, этот показатель определит величину тока, которую сможет отключить автомат. Все номиналы носят стандартный характер. Их диапазон составляет от 3000 до 10 000 А.
Учитывая этот тип, подбор автомата проводят в соответствии с расстоянием, на котором расположена подстанция. Если она находится на значительном удалении, то в квартире или доме устанавливают автомат на 6000 А. При близком расположении подстанции используют аппарат на 10 000 А.
Корпус снабжен квадратиком, в который заключена цифра, характеризующая это значение.
Величина рабочего отключения нанесена на корпус прибора и заключено в квадрат- Классность по токоограничению.
Ток становится максимальным при коротком замыкании через определенное время. Чем быстрее отключится питание, тем меньше шансов получить повреждение. Градация классности в этом плане выражается значениями от 1 до 3. Лучшим является третий класс. Он быстрее всех отключит линию. Несмотря на то, что цена на такие устройства самая высокая, они надежнее всех.
- Характеристика температурного режима.
Практически все автоматы предназначаются для работы в помещении. Температурный разброс составляет от -5 до +35 градусов. Корпус таких приборов не имеет никакой, связанной с этим маркировки. Но есть и такие устройства, которые устанавливаются в щитках на улице. Температурный диапазон у них немного шире и составляет от -25 до +40 градусов. На корпус таких приборов нанесен специальный знак.
Подключение автомата
Обычно с подключением не возникает никаких сложностей. Крепиться автомат может разными способами, но наиболее распространенным вариантом является крепление на DIN-рейку. На ней имеются специальные выступы, которые и удерживают устройство:
Совет №2: Автомат следует подключать с помощью проводов, имеющих изоляцию.
Выбор сечения определяется номиналом. Схема нанесена на корпус.
Проверка работоспособности выполняется после установки автомата. На корпусе имеется кнопку «Тест». После ее нажатия должно произойти срабатывание. Если этого не случилось, проверяется точность подключения. Если все сделано правильно, но срабатывания не происходит, то это свидетельствует о неисправности прибора.
Читайте также статью ⇒ Причины срабатывания дифавтомата.
Варианты схем
Схем существует достаточно много. Все они подходят для любых условий в плане удобства и безопасности. Наличие простых схем предполагает минимальные затраты. Они используются там, где присутствует минимум бытовой техники (дачный коттедж).
Самая простая схема
Используется тогда, когда нет необходимости в установке множества защитных устройств. Вполне достаточной будет установка лишь одного входного автомата. Другое устройство будет относиться к розеточным группам и осветительной линии.
Схема подключения дифференциального автомата, отличающаяся наибольшим удобством и простотой исполненияВариант с большей надежностью
Часто приходится ставить автомат применительно к помещениям «мокрой» группы (ванная). Здесь уже нужна большая безопасность.
Надежная схема, применяющаяся преимущественно для помещений с повышенным уровнем влажностиСелективный вариант
Разветвленная сеть предполагает еще более надежную дорогостоящую систему. Здесь устанавливаются автоматы с классностью S или G. В отношении каждой группы устанавливается отдельный автомат.
Подключение дифференциального автомата по селективной схеме для каждой группы нагрузокЕсли отключится лишь одно какой-то один прибор, оставшиеся будут функционировать.
Ошибки при подключении и монтаже
Частой ошибкой является несоблюдение указанной в паспорте устройства схемы подключения.
Нередко встречается также и ошибочное соединение нуля и защитного проводника за дифавтоматом.
Еще одной ошибкой является неполнофазное подключение, при котором фаза соединяется с устройством, а ноль подключается непосредственно к нулевой шине.
Также зачастую осуществляется подключение нулевой жилы к общей шине после автомата.
Ошибочным также является соединение нулей от различных автоматов в распределительной коробке.
Оцените качество статьи:
От: Стивен Вольфрам, Новый вид науки История клеточных автоматов. Несмотря на их очень простую конструкцию, примерно в 1950-х годах ничего похожего на обычные клеточные автоматы не рассматривалось ранее. Тем не менее, в 1950-е годы, во многом вдохновленные появлением электронных компьютеров, были независимо представлены несколько различных видов систем, эквивалентных клеточным автоматам.Можно идентифицировать множество прекурсоров. Операции с последовательностями цифр использовались с древних времен в арифметических вычислениях. Конечно-разностные приближения к дифференциальным уравнениям начали появляться в начале 1900-х годов и были довольно хорошо известны к 1930-м годам. И машины Тьюринга, изобретенные в 1936 году, основывались на размышлении о произвольных операциях над последовательностями дискретных элементов. (Такие понятия в физике, как модель Изинга, по-видимому, не оказали прямого влияния.) Самый известный способ введения клеточных автоматов (и который в конечном итоге привел к их названию) заключался в работе Джона фон Неймана. разработать абстрактную модель самовоспроизведения в биологии – тему, которая возникла в результате исследований в области кибернетики.Примерно в 1947 году – возможно, на основе химической инженерии – фон Нейман начал с размышлений о моделях, основанных на трехмерных фабриках, описываемых уравнениями в частных производных. Две непосредственные нити возникли из работы фон Неймана. Первый, в основном в 1960-х годах, был все более причудливым обсуждением создания реальных самовоспроизводящихся автоматов – часто в форме космических кораблей. Второй был попыткой лучше понять суть самовоспроизведения с помощью математических исследований детальных свойств клеточных автоматов.В течение 1960-х годов были найдены конструкции для все более простых клеточных автоматов, способных к самовоспроизведению (см. Стр. 1186) и универсальным вычислениям (см. Стр. 1121). К концу 1950-х годов было отмечено, что клеточные автоматы можно рассматривать как параллельные компьютеры, и особенно в 1960-х годах последовательность все более подробных и технических теорем – часто аналогичных теоремам о машинах Тьюринга – была доказана относительно их формальных вычислительных возможности.В конце 1960-х годов начали предприниматься попытки связать клеточные автоматы с математическими обсуждениями динамических систем – хотя, как обсуждается ниже, на самом деле это уже было сделано десятью годами ранее, с другой терминологией. К середине 1970-х работа над клеточными автоматами стала в основном эзотерической, и интерес к ней в значительной степени угас. (Некоторые работы, тем не менее, продолжались, особенно в России и Японии.) Обратите внимание, что даже в информатике использовались различные имена для клеточных автоматов, включая автоматы тесселяции, клеточные пространства, итерационные автоматы, однородные структуры и универсальные пространства. Как упоминалось в основном тексте, к концу 1950-х годов уже существовали всевозможные универсальные компьютеры, на которых было бы легко выполнить моделирование клеточных автоматов. Но по большей части эти компьютеры использовались для изучения традиционных гораздо более сложных систем, таких как уравнения в частных производных. Несмотря на отсутствие научных исследований, один пример клеточного автомата действительно широко вошел в развлекательные вычисления в начале 1970-х годов. Очевидно, частично мотивированный вопросами математической логики, а частично работой Улама и других над «играми-симуляторами», Джон Конвей в 1968 году начал проводить эксперименты (в основном вручную, но позже на компьютере PDP-7) с различными различные правила двумерного клеточного автомата, и к 1970 году он придумал простой набор правил, которые он назвал «Игра в жизнь», которые демонстрируют ряд сложного поведения (см. стр. 249).Во многом благодаря популяризации в Scientific American Мартина Гарднера, Life стала широко известна. Огромное количество усилий было потрачено на поиск особых начальных условий, которые дают определенные формы повторяющегося или другого поведения, но практически не было проведено систематической научной работы (возможно, отчасти потому, что даже Конвей относился к системе в значительной степени как к отдыху), и почти без исключения только когда-либо исследовались очень конкретные правила Жизни. Совершенно оторванные от всего этого, даже в 1950-х годах определенные типы двумерных и одномерных клеточных автоматов уже использовались в различных электронных устройствах и специализированных компьютерах. Фактически, когда в середине 1950-х годов стала выполняться цифровая обработка изображений (для таких приложений, как оптическое распознавание символов и подсчет микроскопических частиц), правила двумерных клеточных автоматов обычно использовались для удаления шума. И в течение нескольких десятилетий, начиная с 1960 года, была построена длинная линия так называемых клеточных логических систем для реализации двумерных клеточных автоматов, в основном для обработки изображений.Большинство используемых правил были специально настроены для обеспечения простого поведения, но иногда отмечалось, что это в значительной степени развлекательный вопрос, который, например, мог генерироваться шаблонами чередующихся полос («кластеризация»). В конце 1950-х – начале 1960-х годов схемы электронной миниатюризации и ранние интегральные схемы часто основывались на наличии идентичных логических элементов, размещенных на линиях или сетках для формирования так называемых ячеистых массивов. В начале 1960-х годов был интерес к итерационным массивам, в которых данные будут многократно проходить через такие системы.Но появилось несколько принципов проектирования, и технология изготовления микросхем с более сложными и менее однородными схемами быстро развивалась. Тем не менее, начиная с 1960-х годов, идея создания массивов или параллельных компьютеров неоднократно появлялась, особенно в таких системах, как ILLIAC IV 1960-х и 1970-х годов, а также систолические массивы и различные массивно-параллельные компьютеры 1980-х годов. Однако обычно правила, придуманные для каждого элемента таких систем, намного сложнее, чем для любого из рассматриваемых мной простых клеточных автоматов. По крайней мере, с начала 1940-х годов электронные или другие цифровые линии задержки или регистры сдвига были обычным способом хранения данных, таких как цифры чисел, а к концу 1940-х годов было отмечено, что так называемые регистры сдвига с линейной обратной связью (см. стр.976) может генерировать сложные выходные последовательности. Эти системы оказываются по существу одномерными аддитивными клеточными автоматами (как правило 90) с ограниченным числом ячеек (сравните стр. 259). Обширный алгебраический анализ их поведения проводился начиная с середины 1950-х годов, но большая часть его была сосредоточена на таких вопросах, как периоды повторения, и даже не выявил явно вложенных шаблонов.(Связанный анализ линейных повторений над конечными полями был выполнен в нескольких случаях в 1800-х годах и более подробно в 1930-х.) Общие одномерные клеточные автоматы связаны с нелинейными регистрами сдвига с обратной связью, и некоторые их исследования, в том числе неожиданно близкие к правилу 30 (см. стр. 1093) – были созданы Соломоном Голомбом с использованием специального оборудования в 1956-1959 годах для применения в устойчивом к помехам радиоуправлении – хотя опять же с упором на такие вопросы, как периоды повторения. Регистры сдвига с линейной обратной связью быстро стали широко использоваться в приложениях связи.Регистры сдвига с нелинейной обратной связью, кажется, широко использовались для военной криптографии, но, несмотря на постоянные слухи, подробности того, что было сделано, по-прежнему остаются в секрете. В чистой математике бесконечные последовательности нулей и единиц рассматривались в различных формах, по крайней мере, с конца 1800-х годов. Начиная с 1930-х годов развитие символической динамики (см. Стр. 963) привело к исследованию отображения таких последовательностей на самих себя. К середине 1950-х годов проводились исследования (в частности, Густав Хедлунд) так называемых блочных карт с коммутацией сдвигов, которые оказались в точности одномерными клеточными автоматами (см. Определенные типы клеточных автоматов также возникали – обычно под разными названиями – в широком диапазоне ситуаций. В конце 1950-х и начале 1960-х годов то, что по сути было одномерными клеточными автоматами, изучались как способ оптимизации схем для арифметических и других операций.Начиная с 1960-х годов, моделирующие идеализированные нейронные сети в некоторых × имели нейроны, связанные с соседями по сетке, что давало двумерный клеточный автомат. Точно так же различные модели активных сред – особенно сердца и других мышц – и процессов реакции-диффузии использовали дискретную сетку и дискретные состояния возбуждения, соответствующие двумерному клеточному автомату. (В физике дискретные идеализации статистической механики и динамические версии систем, таких как модель Изинга, были в некоторой степени близки к клеточным автоматам, за исключением того решающего различия, что случайность встроена в их основные правила.Аддитивные клеточные автоматы, такие как правило 90, неявно возникли в исследованиях биномиальных коэффициентов по модулю простых чисел в 1800-х годах (см. Стр. 870), но также появились в различных условиях, таких как «леса низкорослых деревьев», изученные около 1970 года. К концу 1970-х годов, несмотря на все эти разные направления, исследования систем, эквивалентных клеточным автоматам, в значительной степени прекратились. То, что это должно было произойти как раз в то время, когда компьютеры впервые стали широко доступны для исследовательской работы, является иронией.Но в каком-то смысле это было удачно, потому что это позволило мне, когда я начал работать над клеточными автоматами в 1981 году, определить поле по-новому (хотя, к моему более позднему сожалению, я решил – в попытке признать историю – использовать имя «клеточные автоматы» для изучаемых мной систем). Стивен Вольфрам, Новый вид науки (Wolfram Media, 2002), стр. 876. |
(PDF) На клеточном автомате с временной задержкой для моделирования раковых опухолей
[7] Берталан Ф.Д., Шахтер Р., Али Дж. И Ингимундсон Дж. К., Митотическая скорость и время удвоения внутрибрюшинного
подкожная опухоль Эрлиха, асцит Эрлиха. 1965 Cancer Research 25 685.
[8] Baserga R, Взаимосвязь клеточного цикла с ростом опухоли и контролем клеточного деления: Обзор, 1965
Cancer Research 25 5 581.
[9] Hatfield DL, Yoo M -H, Carlson BA и Gladyshev VN, Селенопротеины, которые действуют в профилактике рака
и продвижение, 2009 Biochimica et Biophysica Acta 1790 1541.
[10] Венкатесваран V, Klotz LH and Fleshner NE, Селеновая модуляция клеточной пролиферации и клеточного цикла
биомаркеров в клеточных линиях карциномы простаты человека, 2002 Cancer Research 62 2540.
[11] Wheldon TE, 1988 Mathematical Models in Cancer Research, Taylor and Francis.
[12] Морейра Дж. И Дойч А., Клеточные автоматные модели развития опухолей: критический обзор, 2002 г. Успехи
в сложных системах 5247.
[13] Вольфрам С., 1986 Теория и приложения клеточных автоматов, Мировая наука.
[14] Маллет Д.Г. и Де Пиллис Л.Г., Модель клеточного автомата взаимодействий опухолево-иммунной системы, 2006 Журнал
Теоретической биологии 239 334.
[15] Гао Д., Цзян Р., Ху S -X, Ван Б. – H и Wu Q -S, Модель клеточного автомата с адаптацией скорости в
в рамках теории трехфазного движения Кернера, 2007 Physical Review E 76 026105.
[16] Копелли М., Роке А. С., Оливейра Р. Ф. и Киноути О. Физика психофизики: Стивенс и Вебер-Фехнер.
Законыявляются передаточными функциями возбудимых сред, Physical Review E 65 060901 (R), 2002.
[17] Manor A и Шнерб Н.В., Происхождение парето-подобных пространственных распределений в экосистемах, Физический обзор 2008 г.
Letters 101 268104.
[18] Судзудо Т. Формирование пространственного паттерна в асинхронных клеточных автоматах с сохранением массы, 2004 г. Физика
А343 185.
[19] Kansal AR, Torquato S, Harsh GR, Chiocca EA и Deisboecke TS, Моделирование роста опухоли головного мозга
динамика с использованием трехмерного клеточного автомата, 2000 Журнал теоретической биологии 203 367.
[20] Quaranta В., Уивер AM и Каммингс П.Т., Математическое моделирование рака: будущее прогноза
и лечение, 2005 Clinica Chimica Acta 357 173.
[21] Гатенби Р.А., Гавлински Е.Т., Гликолитический фенотип в канцерогенезе и опухолевой инвазии: Исследования с помощью математических моделей
, Исследования рака, 2003 г. 63 3847.
[22] Duchting W и Vogelsaenger T, Недавний прогресс в моделировании и моделировании трехмерной опухоли
рост и лечение, 1985 Biosystems 18 79.
[23] Qi A -S, Zheng X, Du C -Y и An B-S, Модель клеточного автомата ракового роста, 1993 Journal of
Теоретическая биология 161 1.
[24] Патель А.А., Гавлински Е.Т., Лемье С.К. и Гатенби Р.А., Модель клеточного автомата ранней опухоли
рост и инвазия: эффекты васкуляризации нативных тканей и усиление анаэробного метаболизма опухоли,
2001 Journal of Theatical Biology 213 315.
[25] Андерсон А.Р. и капеллан MJ, Непрерывные и дискретные математические модели индуцированного опухолью ангиогенеза
, 1998 Бюллетень математической биологии 60 857.
[26] Рейс Е.А., Сантос LBL и Пинхо STR, Модель клеточного автомата для бессосудистого роста солидной опухоли под
эффект терапии, 2009 Physica A 388 1303.
[27] Бирн HM, Влияние временных задержек на динамику бессосудистого роста опухоли, 1997 Mathematical
Biosciences 144 83.
[28] Цуй С. и Сюй С. Анализ математических моделей роста опухолей с задержкой по времени в клетках.
пролиферация, 2007 г. Журнал математического анализа и приложений 336 523.
[29] Стил Г.Г., 1977 г. Кинетика роста. опухолей, Оксфорд: Clarendon Press.
[30] Банерджи С. и Саркар Р.Р., Модель задержки, индуцированная опухольиммунным взаимодействием и контроль злокачественной опухоли
, рост опухоли, 2008 Biosystems 91 268.
[31] Томлинсон Р., Измерение и лечение карциномы груди, 1982 Клиническая радиология 33 481.
[32] Вилласана М. и Радунская А., Модель дифференциального уравнения задержки для роста опухоли, 2003 Математический
Биология 47 270.
[33] Юань З., Ху Д. и Хуанг Л., Анализ стабильности и бифуркации на дискретных объектах. временная система двух нейронов,
2004 Applied Mathematics Letters 17 1239.
[34] Хошен Дж. и Копельман Р. Перколяция и распределение кластеров. I. Метод множественной маркировки кластеров и алгоритм критической концентрации
, Physical Review B 14 8 3438, 1976 г.
[35] Мендес Р.Л., Сантос А.А., Мартинс М.Л. и Вилела М.Дж., Распределение кластеров клеточных агрегатов в культуре по размеру,
2001 Physica A 298 471.
[36] Ватанабэ С. 72 215.
[37] Эванс К. В., Метастатическая клетка, 1991 г. Поведение и биохимия, Чепмен и Холл, Лондон.
[38] Стиг П. С., Метастаз опухоли: понимание механизмов и клинические проблемы, 2006 Nature Medicine 12 8 895.
Dynamic Days South America 2010 IOP Publishing
Journal of Physics: Conference Series 285 (2011) 012015 doi: 10.1088 / 1742-6596 / 285/1/012015
Моделирование топологических эффектов на динамику мотивов с прямой связью на клеточных автоматах | Journal of Biological Engineering
В центре внимания нашего анализа было изучение того, как топология сети влияет на динамику процессов в различных мотивах прямой связи. Чтобы гарантировать, что анализируемые сети были сопоставимы, чтобы позволить идентифицировать устойчивые закономерности структуры-динамики, мы предположили, что (i) константы скорости для всех процессов равны, (ii) начальные условия выбраны так, чтобы источник (S ) изначально в пять раз больше, чем каждый из других видов, и (iii) все ферментные активности постоянны и равны.Мы построили схему, содержащую все десять мотивов с четырьмя узлами (рис.6) и их взаимные преобразования (15 добавлений ребра с образованием нового цикла и три смены направления звеньев, соединяющих мотивы прямой связи с би- и три- параллельные) и выполнили как линейное, так и нелинейное моделирование CA и ODE. Каждая сеть порождает систему из четырех линейных ОДУ, которые можно решить явно. В нелинейном случае мы провели численное моделирование как с необратимыми, так и с обратимыми первыми шагами реакции.Во всех версиях моделей ODE сети были ранжированы в соответствии с их 90% -ным временем преобразования. Числовые значения ODE обозначают время, измеренное в произвольных единицах, необходимое для 90% полного преобразования исходной подложки S в целевой продукт T .
Чтобы гарантировать, что анализируемые сети были сопоставимы, чтобы позволить идентифицировать устойчивые закономерности структуры-динамики, мы предположили, что (i) константы скорости для всех процессов равны, (ii) начальные условия выбраны так, чтобы источник (S ) изначально в пять раз больше, чем каждый из других видов, и (iii) все ферментные активности постоянны и равны.Мы построили схему, содержащую все десять мотивов с четырьмя узлами (рис.6) и их взаимные преобразования (15 добавлений ребра с образованием нового цикла и три смены направления звеньев, соединяющих мотивы прямой связи с би- и три- параллельные) и выполнили как линейное, так и нелинейное моделирование CA и ODE. Каждая сеть порождает систему из четырех линейных ОДУ, которые можно решить явно. В нелинейном случае мы провели численное моделирование как с необратимыми, так и с обратимыми первыми шагами реакции.Во всех версиях моделей ODE сети были ранжированы в соответствии с их 90% -ным временем преобразования. Числовые значения ODE обозначают время, измеренное в произвольных единицах, необходимое для 90% полного преобразования исходной подложки S в целевой продукт T .
Диаграмма всех десяти четырехузловых мотивов (восемь с прямой связью и F – бипараллельная) преобразования исходного узла S в целевой узел T: A – линейный, B , C , D , E , G и H – прямая связь, F и J – двухпараллельная и I – трехпараллельная.Мотивы упорядочены в соответствии с их динамической эффективностью в производстве целевого продукта с наивысшей скоростью, оцениваемой по уменьшению количества итераций и уменьшению времени, как это производится линейной (LDE) и нелинейной моделями ODE для 90% -ного преобразования S → T. Нелинейные необратимые и обратимые времена ODE обозначаются NDE и NDE ‘соответственно. Взаимные преобразования показанных структур включают 15 добавлений еще одной прямой связи, в то время как те, которые отмечены звездочкой (преобразования D → F , E → I и J → H ), включают обращение одного направление ссылки.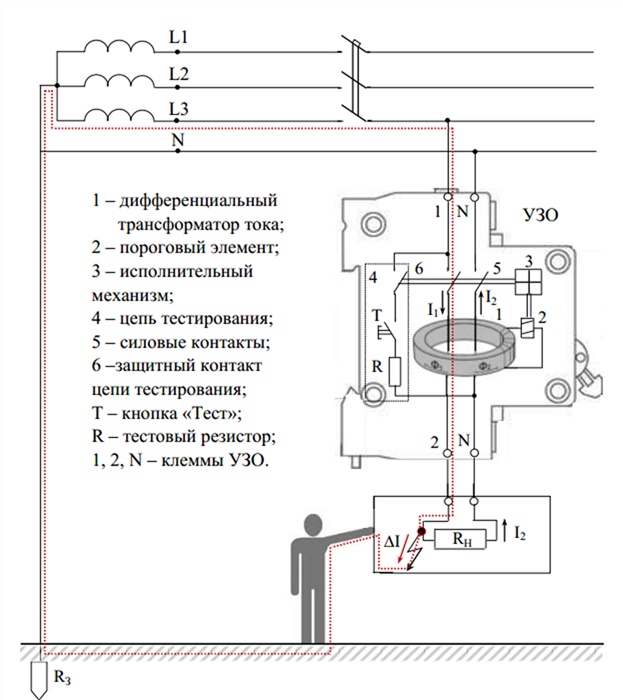
Сравнение эффективности работы десяти четырехузловых сетей (рис. 6) показывает, что CA и линейное ODE упорядочивают мотивы одинаково, за небольшим исключением. А именно, CA ранжирует структуры H, и I с одинаковым наивысшим коэффициентом конверсии (2408 ± 13 и 2427 ± 15, соответственно), поскольку номера итераций перекрываются в пределах их стандартных отклонений. Линейное ODE также оценивает H и I как самые быстрые четырехузловые топологии, добавляя третью структуру G , не только показывающую то же время преобразования 2.17, но на этот раз T (t) определяется по одной и той же формуле во всех трех случаях (уравнение 17).
Нелинейные модели ODE с обратимыми и необратимыми первыми шагами производят идентичный порядок десяти структур. Это совпадает с порядком первых семи структур, описанных выше CA и линейными ODE, при этом предполагается, что сеть I является самой быстрой, G и H имеют очень близкие характеристики, H показаны как немного медленнее, чем Г .
Топологический анализ девяти сетей выявил некоторые полезные закономерности их динамики. Хотя анализируемые здесь сети относительно просты, они могут быть полезны при анализе локальной топологии в больших сложных сетях. Некоторые из наблюдаемых топодинамических паттернов описаны ниже.
Динамический шаблон прямой связи 1 (DFFP1)
Чем короче расстояние графа d (S → T) между исходным узлом и целевым узлом в мотиве прямой связи, тем выше общий коэффициент конверсии:
A (d = 3)
Обратите внимание, что бипараллельные мотивы F и J не подчиняются этому неравенству скорости.
Динамический шаблон прямой связи 2 (DFFP2)
Чем короче средняя длина пути l (S → T) между исходным узлом и целевым узлом в мотиве прямой связи, тем выше общий коэффициент конверсии:
А ( л = 3)
Учет всех путей S → T является немного более чувствительным шаблоном, который выделяет сеть I как наиболее эффективную четырехузловую структуру в соответствии с результатом, полученным с помощью нелинейной модели ODE. Бипараллельные мотивы F и J не подчиняются этой топодинамической тенденции с прямой связью, которая более важна в более крупных сетях, где количество путей S → T быстро увеличивается.
Бипараллельные мотивы F и J не подчиняются этой топодинамической тенденции с прямой связью, которая более важна в более крупных сетях, где количество путей S → T быстро увеличивается.
Динамический шаблон прямой связи 3 (
изодинамичность )Некоторые мотивы прямой связи с разной топологией производят одинаковую общую скорость преобразования S → T в моделях CA и линейных ODE:
CA: H (2408 ± 13) = I (2427 ± 15)
ODE: G = H = I = 2.1600
Ур. (16b) следует из аналитического решения линейных дифференциальных уравнений для конструкций G , H и I :
T (t) = 1−78e − tMathType @ MTEF @ 5 @ 5 @ + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH92BBBBB1xD2x05BBB1x0BBIx0BBIx0BBBBBBIxDBX xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemivaqLaeiikaGIaemiDaqNaeiykaKIaeyypa0JaeGymaeJaeyOeI0scfa4aaSaaaeaacqaI3aWnaeaacqaI4aaoaaGccqWGLbqzdaahaaWcbeqaaiabgkHiTiabdsha0baaaaa @ 39D8 @(17)
Линейные ОДУ также классифицируют мотивы F и J как изодинамические, подчиняясь одному и тому же кинетическому уравнению:
T (t) = 1−32e − t + 58e − 2tMathType @ MTEF @ 5 @ 5 @ + = feaafiart1ev1aaaatCvAuWrPxaatCvAuVrPh1 xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemivaqLaeiikaGIaemiDaqNaeiykaKIaeyypa0JaeGymaeJaeyOeI0scfa4aaSaaaeaacqaIZaWmaeaacqaIYaGmaaGccqWGLbqzdaahaaWcbeqaaiabgkHiTiabdsha0baakiabgUcaRKqbaoaalaaabaGaeGynaudabaGaeGioaGdaaOGaemyzau2aaWbaaSqabeaacqGHsislcqaIYaGmcqWG0baDaaaaaa @ 421E @(18)
Моделирование CA и нелинейного ODE показало, что эти два мотива имеют разную, хотя и относительно близкую эффективность, причем структура J является более медленной:
CA: J (3348 ± 18)
Необратимое нелинейное ОДУ: J (6.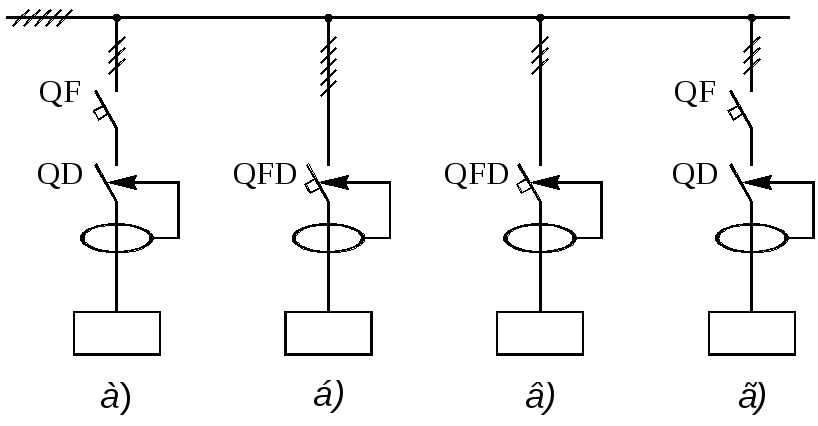 05)
05)
Обратимое нелинейное ОДУ: J (9,00)
Линейное ОДУ: J (2,679) = F (2,679)
Свойство изодинамичности – это удивительно новый сетевой паттерн, который может потребовать дальнейших подробных исследований.
Динамическая схема прямой связи 4 (DFFP4)
Любое замыкание кольца линейной цепочки преобразования исходной подложки S в целевой продукт T ускоряет преобразование.Ускорение процесса наиболее сильно, когда прямая связь напрямую соединяет субстрат с мишенью, и наименьшее, когда связь соединяет субстрат с промежуточным продуктом (рис. 7, 8).
Рисунок 7Топологические преобразования с прямой связью (1, 2 и 3) всегда ускоряют процессы, описанные как линейная цепочка событий. Показаны различные механизмы замыкания кольца, самая быстрая топология – это топология с прямым каналом прямой связи Источник → Цель.Линейные и нелинейные необратимые и обратимые времена ODE обозначаются как LDE, NDE и NDE ‘соответственно.
Рисунок 8Добавление второй кромки прямой связи всегда ускоряет процессы в мотиве прямой связи. Такой общей схемы для добавления третьего звена прямой связи не существует (сравните E → G с H → G ). Линейные и нелинейные необратимые и обратимые времена ODE обозначаются как LDE, NDE и NDE ‘соответственно.
A
Замыкающие кольца, описываемые этим шаблоном, показаны на рис.7 с порядковыми номерами 1, 2 и 3. Общность этого отношения топологии и динамики была проверена для всей серии FFA, FFB и FFC (рис. 5), имеющей до десяти узлов мотива. Во всех случаях было обнаружено, что стандартное отклонение числа итераций СА более чем на два порядка меньше этого числа. Этот шаблон выходит за рамки простых топологических шаблонов 1 и 2, показанных выше, которые не позволяют различать серии FFB и FFC.
Динамический шаблон прямой связи 5 (DFFP5)
Добавление второй кромки прямой связи ( мотив двойной прямой связи ) между любой парой узлов на более длинном пути цикла FF ускоряет динамику конверсия исходного субстрата в целевой продукт (рис.8).
D
Эти неравенства для количества итераций, проиллюстрированные на рис. 8 с четырьмя узлами, были проверены и признаны действительными без исключений для всех размеров трех исследованных серий FF (от четырех до десяти узлов петли). Сравнивая серии FFF и FFE, можно сделать вывод, что ускорение преобразования подложки в цель выше, когда вторая FF-ссылка начинается в узле, расположенном на более длинном пути исходный-целевой, и заканчивается в целевом узле, а не в начинаются в исходном узле и заканчиваются другим узлом перед целевым.Поскольку структуры мотива FFG с тройной прямой связью (см. График G на фиг. 8) объединяют тенденции CA серий FFF и FFE, ускорение в этой серии является промежуточным между ускорением FFE и FFF. Однако модели ODE не подтверждают этот результат с линейной моделью, показывающей, что G и H изодинамичны, тогда как две нелинейные модели показывают G как немного более эффективный, чем H. Следовательно, добавление третьей прямой связи не обязательно приводит к ускорения и стабильной тенденции нет.
Динамический шаблон прямой связи 6 (DFFP6)
Изменение направления одного или нескольких каналов в мотиве прямой связи на обратное, чтобы превратить его в бипараллельный и трехпараллельный, увеличивает эффективность сети. (Рис.6, 9).
Рисунок 9При том же количестве узлов мотив прямой связи медленнее, чем бипараллельный мотив. Топология, обеспечивающая самую быструю динамику, – это тройной параллельный мотив I .
с прямой связью <би-параллель <три-параллель
Три таких преобразования:
D
показаны на рис.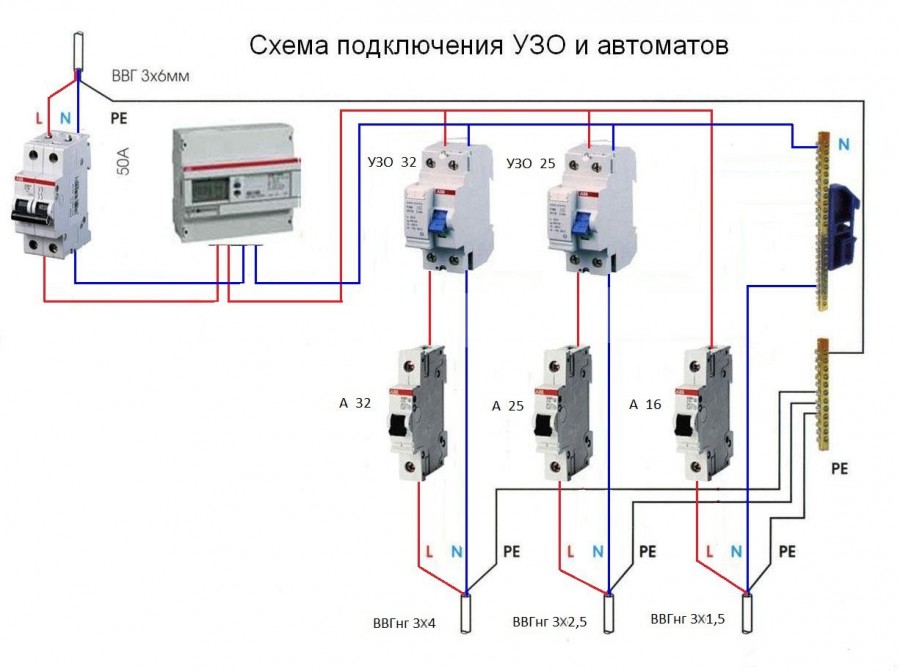 6, где они отмечены звездочками.
6, где они отмечены звездочками.
Квантовые блуждания и клеточные автоматы Дирака на программируемом квантовом компьютере с захваченными ионами
Обзор квантовых блужданий и связь с уравнением Дирака
DQW состоит из двух квантово-механических систем, эффективной монеты и позиционного пространства пешехода , а также оператор эволюции, который применяется к обеим системам с дискретными временными шагами. Эволюция задается унитарным оператором, определенным на тензорном произведении двух гильбертовых пространств \ ({{\ mathcal {H}}} _ {{\ rm {c}}} \ otimes {{\ mathcal {H}}} _ {{\ rm {p}}} \), где \ ({{\ mathcal {H}}} _ {{\ rm {c}}} \) – гильбертово пространство монеты, натянутое на внутренние состояния \ ({\ left | 0 \ right \ rangle} _ {{\ rm {c}}} \) и \ ({\ left | 1 \ right \ rangle} _ {{\ rm {c}}} \) одного кубита, в то время как \ ({{\ mathcal {H}}} _ {p} \) представляет положение в гильбертовом пространстве, заданное состояниями положения \ (\ left | x \ right \ rangle \) с \ (x \ in {\ mathbb { Z}} \), закодированный в несколько кубитов, как описано ниже.Здесь унитарная квантовая операция подбрасывания монеты, \ ({\ hat {C}} _ {\ theta} \), является унитарным оператором вращения, который действует в пространстве кубитов монеты,
$$ {\ hat {C}} _ {\ theta} = \ left [\ begin {array} {cc} \ cos \ theta & -i \ sin \ theta \\ -i \ sin \ theta & \ cos \ theta \ end {array} \ right] \ otimes {\ hat {I}} _ {{\ rm {p}}}, $$
(1)
, где θ – параметр смещения монеты, который может изменяться на каждом шаге для изменения весов наложения путей QW.Оператор условного сдвига позиции \ (\ hat {S} \) переводит частицу влево и вправо в зависимости от состояния кубита монеты,
$$ \ hat {S} = {\ left | 0 \ right \ rangle} _ {{\ rm {c}} \, {\ rm {c}}} \ langle 0 | \ otimes \ sum _ {x \ in {\ mathbb {Z}}} | x-1 \ rangle {\ langle x | + | 1 \ rangle} _ {{\ rm {c}} \, {\ rm {c}}} \ langle 1 | \ otimes \ sum _ {x \ in {\ mathbb {Z}}} | x + 1 \ rangle \ left \ langle x \ right |. $$
$$
(2)
Состояние частицы в позиционном пространстве после t шагов блуждания достигается повторным действием оператора \ (\ hat {W} = \ hat {S} {\ hat {C}} _ { \ theta} \) от начального состояния частицы \ ({\ left | \ psi \ right \ rangle} _ {{\ rm {c}}} = \ alpha {\ left | 0 \ right \ rangle} _ { {\ rm {c}}} + \ beta {\ left | 1 \ right \ rangle} _ {{\ rm {c}}} \) в позиции x = 0, как показано на рис.{2} \).
Рис.1: Схема квантового блуждания в дискретном времени .Каждый шаг состоит из операции квантовой монеты, \ ({\ hat {C}} _ {\ theta} \), с настраиваемыми параметрами эффективного смещения монеты, θ i , за которой следует операция сдвига , \(\шляпы}\).
Недавние работы показали связь между DQW и уравнением Дирака 14,15,16,17,18,43 . Начиная с оператора эволюции в дискретном времени и затем переходя из пространства позиций в пространство импульсов, кинематика Дирака может быть восстановлена из диагональных членов унитарного оператора эволюции для малых импульсов в режиме малых масс 16,17,18 .В отличие от этих предложений в системе Фурье, мы фокусируем нашу реализацию на распределении вероятностей ДКЯ, которое аналогично распространению релятивистской частицы. Для реализации DCA и восстановления уравнения Дирака используется квантовое блуждание с разделением шагов, одна из форм DQW 40 . Каждый шаг квантового блуждания с разделением шагов представляет собой композицию двух полушаговых эволюций с разными смещениями монет и операторами позиционного сдвига:
$$ {\ hat {W}} _ {{\ rm {ss}}} = { \ hat {S}} _ {+} {\ hat {C}} _ {{\ theta} _ {2}} {\ hat {S}} _ {-} {\ hat {C}} _ {{\ theta} _ {1}}, $$
(4)
, где монетная операция \ ({\ hat {C}} _ {\ theta} _ {j}} \) с j = 1, 2 дана в уравнении. {2} / 2) {\ sigma} _ {z} {\ partial} _ {x} + i {\ theta} _ {2 } {\ sigma} _ {x}] \ Psi (x, t) \ приблизительно 0 \).
{2} / 2) {\ sigma} _ {z} {\ partial} _ {x} + i {\ theta} _ {2 } {\ sigma} _ {x}] \ Psi (x, t) \ приблизительно 0 \).
В то же время, выбирая θ 1 = 0, оператор квантового блуждания \ ({\ hat {W}} _ {{\ rm {ss}}} \), заданный в уравнении. (4) принимает форму унитарного оператора для DCA 40 ,
$$ {\ hat {W}} _ {{\ rm {ss}}} = \ left [\ begin {array} {cc} \ cos ({\ theta} _ {2}) {S} _ {-} & – i \ sin ({\ theta} _ {2}) {\ mathbb {1}} \\ -i \ sin ({\ theta} _ {2}) {\ mathbb {1}} & \ cos ({\ theta} _ {2}) {S} _ {+} \ end {array} \ right] = {U} _ {{\ rm {DCA}}}. $$
(8)
В этих рамках θ 2 определяет массу дираковской частицы.Двухшаговый DQW, описываемый оператором \ ({\ hat {W}} _ {\ rm {ss}}} \), эквивалентен двухпериодному DQW с альтернативными монетными операциями, θ 1 и θ 2 , когда альтернативные точки в позиционном пространстве с нулевой вероятностью игнорируются 47 . Следовательно, вся динамика DCA может быть восстановлена из эволюции DQW с помощью \ (\ hat {W} \) и чередования двух операций с монетами. См. В разделе Методы сравнения DCA и явного решения уравнения Дирака.Типичные особенности уравнения Дирака в релятивистской квантовой механике, такие как Zitterbewegung 40 и парадокс Клейна 48 , также являются динамическими особенностями DCA, а также расширением вероятностного распределения и запутыванием локализованных положительных значений. энергетические состояния. Отметим, что эти эффекты также были показаны в прямом аналоговом моделировании уравнения Дирака с захваченными ионами 35 и BEC 49 .
Экспериментальная реализация DQW
Чтобы реализовать DQW на системе кубитов, необходимо выбрать отображение положения частицы в пространство кубитов.Как показано в 50 , не существует уникального способа сопоставить состояния положения с состояниями нескольких кубитов, поэтому разложение каждой схемы зависит от принятой конфигурации. Прямое отображение каждой позиции ходока в один кубит в цепочке, имитирующее расположение массива кубитов, неэффективно с точки зрения количества кубитов и требуемых вентилей (первый растет линейно, а второй – квадратично с моделируемым размером пространства позиций). Чтобы свести к минимуму использование ресурсов, мы используем преимущества цифрового представления для отображения пространства позиций в многокубитовое состояние и переупорядочиваем его таким образом, чтобы состояние \ (\ left | 0 \ right \ rangle \, ( \ left | 1 \ right \ rangle) \) последнего кубита соответствует четным (нечетным) номерам позиций.Это позволяет минимизировать изменения, необходимые в конфигурации пространства кубитов на каждом этапе обхода (см. Рис. 2). Для реализации квантового блуждания в одномерном положении требуется гильбертово пространство размером 2 n , ( n + 1) кубитов. Один кубит действует как монета, а другие n кубитов имитируют позиционное гильбертово пространство с 2 n – 1 позициями симметричного обхода вокруг \ (\ left | x = 0 \ right \ rangle \). Мы отмечаем, что частица может быть запущена из любой точки позиционного пространства, однако установка начального состояния сокращает подсчет вентилей в схеме и, следовательно, уменьшает общую ошибку.Операция с монетой достигается вращением одного кубита на кубите-монете, в то время как операторы сдвига реализуются с помощью монеты в качестве управляющего кубита для изменения состояния положения во время прогулки.
Прямое отображение каждой позиции ходока в один кубит в цепочке, имитирующее расположение массива кубитов, неэффективно с точки зрения количества кубитов и требуемых вентилей (первый растет линейно, а второй – квадратично с моделируемым размером пространства позиций). Чтобы свести к минимуму использование ресурсов, мы используем преимущества цифрового представления для отображения пространства позиций в многокубитовое состояние и переупорядочиваем его таким образом, чтобы состояние \ (\ left | 0 \ right \ rangle \, ( \ left | 1 \ right \ rangle) \) последнего кубита соответствует четным (нечетным) номерам позиций.Это позволяет минимизировать изменения, необходимые в конфигурации пространства кубитов на каждом этапе обхода (см. Рис. 2). Для реализации квантового блуждания в одномерном положении требуется гильбертово пространство размером 2 n , ( n + 1) кубитов. Один кубит действует как монета, а другие n кубитов имитируют позиционное гильбертово пространство с 2 n – 1 позициями симметричного обхода вокруг \ (\ left | x = 0 \ right \ rangle \). Мы отмечаем, что частица может быть запущена из любой точки позиционного пространства, однако установка начального состояния сокращает подсчет вентилей в схеме и, следовательно, уменьшает общую ошибку.Операция с монетой достигается вращением одного кубита на кубите-монете, в то время как операторы сдвига реализуются с помощью монеты в качестве управляющего кубита для изменения состояния положения во время прогулки.
Мультикубитовые состояния переупорядочены таким образом, что состояние \ (\ left | 0 \ right \ rangle \, (\ left | 1 \ right \ rangle) \) последнего кубита соответствует четному (нечетному ) номера позиций и их соответствие в пространстве позиций.
Мы реализуем блуждание по цепочке из семи отдельных ионов 171 Yb + , заключенных в ловушку Пауля и охлаждаемых лазером близко к их движущемуся основному состоянию 45,51 .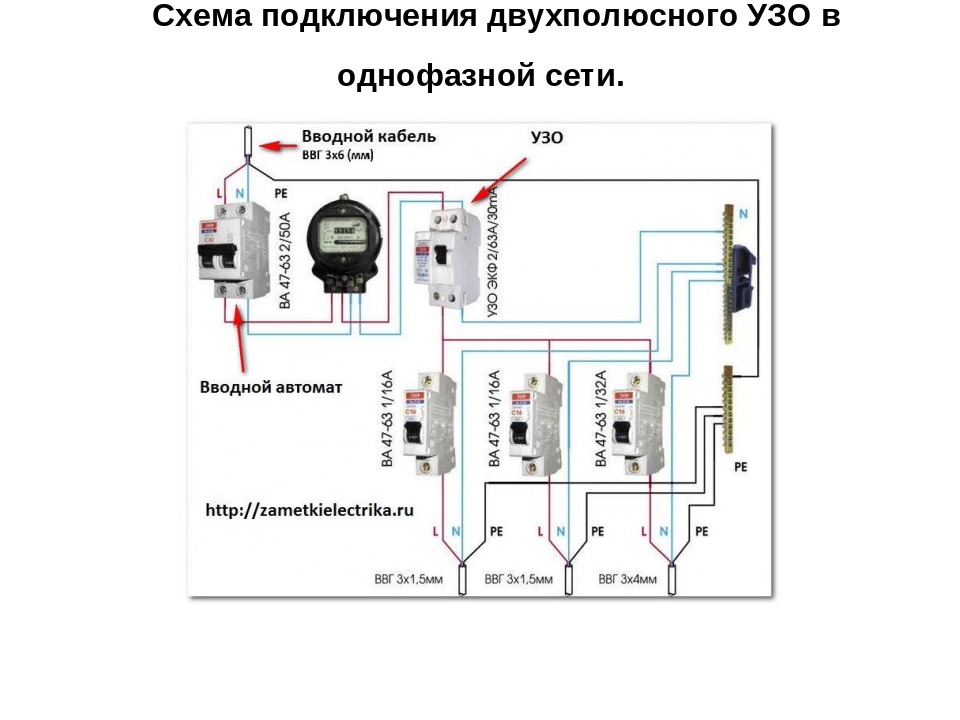 Пять из них используются для кодирования кубитов на их сверхтонком уровне 2 S 1/2 . Вращения одного кубита, или R-вентили, и двухкубитовые запутывающие взаимодействия, или XX-вентили, достигаются путем применения двух встречных оптических рамановских лучей к цепочке, один из которых имеет индивидуальную адресацию (подробности эксперимента см. В Методах).Мы можем представить до 15 позиций симметричной КЯ, включая начальную позицию \ (\ left | x = 0 \ right \ rangle \).
Пять из них используются для кодирования кубитов на их сверхтонком уровне 2 S 1/2 . Вращения одного кубита, или R-вентили, и двухкубитовые запутывающие взаимодействия, или XX-вентили, достигаются путем применения двух встречных оптических рамановских лучей к цепочке, один из которых имеет индивидуальную адресацию (подробности эксперимента см. В Методах).Мы можем представить до 15 позиций симметричной КЯ, включая начальную позицию \ (\ left | x = 0 \ right \ rangle \).
На основе этого позиционного представления составлена принципиальная схема DQW на пяти кубитах с начальным состоянием \ ({\ left | 0 \ right \ rangle} _ {c} \ otimes \ left | 0000 \ right \ rangle \) до пяти шагов, см. рис. 3. Каждый шаг эволюции \ (\ hat {W} \) начинается с операции вращения монеты-кубита \ ({\ hat {C}} _ {{\ theta } _ {j}} \), за которым следует набор управляемых вентилей, которые изменяют состояние положения частицы под \ (\ hat {S} \).Из-за необоснованного выбора используемого представления позиции достаточно выполнять однокубитовый поворот последнего кубита на каждом шаге, что также может быть выполнено классическим трекингом 50 .
Рис. 3: Схема реализации квантовых блужданий на процессоре захваченных ионов и его временная эволюция . a Принципиальная схема DQW и DCA. Каждый пунктирный блок описывает один шаг квантового блуждания. b Квантовая прогулка в дискретном времени. Сравнение экспериментальных результатов (слева) и теоретического распределения вероятностей квантового блуждания (справа) для первых пяти шагов с начальным состоянием частицы b i и b iv \ ({\ left | \ psi \ right \ rangle} _ {{\ rm {c}}} = {\ left | 0 \ right \ rangle} _ {{\ rm {c}}} \), b ii и b iv \ ({\ left | \ psi \ right \ rangle} _ {{\ rm {c}}} = {\ left | 1 \ right \ rangle} _ {{\ rm {c}}} \), b iii и b vi \ ({\ left | \ psi \ right \ rangle} _ {{\ rm {c}}} = {\ left | 0 \ right \ rangle} _ {{\ rm {c}}} + i {\ left | 1 \ right \ rangle} _ {{\ rm {c}}} \) и состояние положения \ (\ left | x = 0 \ right \ rangle \). c Выход клеточного автомата Дирака step-5 для θ 1 = 0 и, c i и c iv θ 2 = π /4, c ii и c v θ 2 = π /10 и c iii и c vi θ 2 = π /20 с начальным состоянием \ (\ left | {\ Psi } _ {{\ rm {in}}} \ right \ rangle = ({\ left | 0 \ right \ rangle} _ {{\ rm {c}}} + i {\ left | 1 \ right \ rangle} _ {{\ rm {c}}}) \ otimes \ left | x = 0 \ right \ rangle \).
c Выход клеточного автомата Дирака step-5 для θ 1 = 0 и, c i и c iv θ 2 = π /4, c ii и c v θ 2 = π /10 и c iii и c vi θ 2 = π /20 с начальным состоянием \ (\ left | {\ Psi } _ {{\ rm {in}}} \ right \ rangle = ({\ left | 0 \ right \ rangle} _ {{\ rm {c}}} + i {\ left | 1 \ right \ rangle} _ {{\ rm {c}}}) \ otimes \ left | x = 0 \ right \ rangle \).
Вычислительные вентили, такие как CNOT, Toffoli и Toffoli-4, генерируются компилятором, который разбивает их на составляющие одно- и двухкубитные вентили физического уровня 45 . Принципиальная схема, подробно описывающая скомпилированные строительные блоки, показана в разделе “Методы”. Чтобы подготовить начальное состояние частицы, отличное от \ ({\ left | 0 \ right \ rangle} _ {{\ rm {c}}} \), достаточно перед первым шагом выполнить вращение монеты-кубита. В некоторых случаях это вращение может быть поглощено первыми воротами на первом этапе.Таблица 1 суммирует количество собственных вентилей, необходимых для каждого шага для начального состояния. Чтобы восстановить эволюцию уравнения Дирака в DQW после пяти шагов, требуется 81 вентиль с одним кубитом и 32 элемента XX.
После эволюции ряда шагов мы производим выборку соответствующего распределения вероятностей 3000 раз и исправляем результаты на предмет ошибок считывания. Для эволюции DQW до пяти шагов, показанных на рис. 3, используется сбалансированная монета ( θ 1 = θ 2 = π /4), где начальное положение равно \ (\ left | x = 0 \ right \ rangle \) для различных начальных состояний частицы, \ ({\ left | 0 \ right \ rangle} _ {{\ rm {c}}} \) на рис.3b i, \ ({\ left | 1 \ right \ rangle} _ {{\ rm {c}}} \) на рис. 3b ii, и их равная суперпозиция на рис. 3b iii. На рис. 3b iv, b v и b vi мы показываем идеальный результат классического моделирования схемы для сравнения (график разницы см. В разделе «Методы»). В сбалансированной монете частица эволюционирует в равной суперпозиции в левую и правую позиции на каждом временном шаге, и при измерении существует 50/50 вероятность нахождения частицы слева или справа от ее предыдущего положения, как и при классическом блуждании. .Если мы позволим DQW развиваться более чем на три шага, прежде чем мы выполним измерение положения, мы обнаружим совершенно другое распределение вероятностей по сравнению с классическим случайным блужданием 52 .
В разделе «Методы»). В сбалансированной монете частица эволюционирует в равной суперпозиции в левую и правую позиции на каждом временном шаге, и при измерении существует 50/50 вероятность нахождения частицы слева или справа от ее предыдущего положения, как и при классическом блуждании. .Если мы позволим DQW развиваться более чем на три шага, прежде чем мы выполним измерение положения, мы обнаружим совершенно другое распределение вероятностей по сравнению с классическим случайным блужданием 52 .
Та же экспериментальная установка может быть использована для восстановления DCA с двухпериодным DQW. Здесь мы установили θ 1 = 0 и изменили θ 2 , чтобы восстановить уравнение Дирака для различных значений массы. На рис. 3в представлены экспериментальные результаты для θ 2 = π /4, π /10 и π /20, соответствующих массе 1.1357, 0,3305 и 0,159 в единицах ℏc −2 s −1 , с начальным состоянием частицы в суперпозиции \ ({\ left | 0 \ right \ rangle} _ {c} + i {\ left | 1 \ right \ rangle} _ {c} \). Основным признаком DCA для малых значений массы является наличие пиков, движущихся наружу, и плоское распределение в середине, как показано для случаев с небольшими значениями θ 2 , рис. 3c ii-iii. Это бимодальное распределение вероятностей в позиционном пространстве указывает на одномерный аналог первоначально локализованной дираковской частицы с положительной энергией, развивающейся во времени, которая распространяется во всех направлениях в позиционном пространстве со скоростью, близкой к скорости света 53 .Напротив, DCA с θ 2 = π /4, рис. 3c i соответствует массивной частице и, следовательно, имеет место медленное распространение, а не баллистическая траектория в пространстве позиций.
Растущие нейронные клеточные автоматы
Содержание
Эта статья является частью
Тема для дифференцируемых самоорганизующихся систем,
экспериментальный формат сбора приглашенных коротких статей, углубляющихся в
дифференцируемые самоорганизующиеся системы с вкраплениями критических
комментарии нескольких экспертов в смежных областях.
Большинство многоклеточных организмов начинают свою жизнь как отдельная яйцеклетка – одиночная клетка, потомство которой надежно самоорганизуется в очень сложные анатомии с множеством органов и тканей в одном и том же расположении каждый раз. Способность строить собственное тело, наверное, самая лучшая. фундаментальный навык, которым обладает каждое живое существо. Морфогенез ( процесс формирования формы организма) является одним из самых ярких Примеры феномена под названием самоорганизация .Клетки, крошечные строительные блоки тел, общаются со своими соседями, чтобы решить форма органов и планы тела, где выращивать каждый орган, как соединить их, и когда в конечном итоге остановиться. Понимание взаимодействия возникновения сложных исходов из простых правил и гомеостатический Саморегулирующиеся петли обратной связи, пытающиеся поддерживать тело в стабильном состоянии или сохранить его правильную общую морфологию при внешнем возмущения петли обратной связи – активная область исследований .Что ясно в том, что эволюция научилась использовать законы физики и вычислений реализовать высоконадежное морфогенетическое программное обеспечение, работающее на кодируемое геномом клеточное оборудование.
Этот процесс чрезвычайно устойчив к возмущениям. Даже когда организм полностью развитые, некоторые виды все еще обладают способностью восстанавливать повреждения – процесс, известный как регенерация. Некоторые существа, например саламандры, могут полностью регенерировать жизненно важные органы, конечности, глаза или даже части мозга! Морфогенез – удивительно адаптивный процесс.Иногда даже очень атипичный процесс развития может привести к появлению жизнеспособного организма – например, когда зародыш раннего млекопитающего разрезать пополам, каждая половина сформирует полный особи – однояйцевые близнецы!
Самая большая загадка в этой области – это вопрос о том, как клеточный коллектив
знает, что строить и когда останавливаться. Науки о геномике и стволовых клетках
биология – это только часть головоломки, поскольку они объясняют распространение
конкретные компоненты в каждой ячейке и создание разных типов
ячеек.Хотя мы знаем о многих генах, которые требуют для
процесса регенерации, мы до сих пор не знаем алгоритм, который достаточно , чтобы клетки знали, как строить или реконструировать сложные органы
к очень конкретной анатомической конечной цели. Таким образом, одна из главных опор будущего
работа в области биомедицины – это открытие процесса, с помощью которого крупномасштабные
анатомия определяется внутри коллективов клеток, и как мы можем это переписать
информация для рационального управления ростом и формой.Это также становится
ясно, что программное обеспечение жизни обладает многочисленными модулями или подпрограммами,
например «Построй глаз здесь», который можно активировать простым сигналом
триггеры. Обнаружение таких подпрограмм и
отображение логики развития – это новая область на пересечении
биология развития и информатика. Следующий важный шаг – попробовать
сформулировать вычислительные модели этого процесса, чтобы обогатить
концептуальный инструментарий биологов и помощь в переводе открытий
биологии в лучшую робототехнику и вычислительные технологии.
Науки о геномике и стволовых клетках
биология – это только часть головоломки, поскольку они объясняют распространение
конкретные компоненты в каждой ячейке и создание разных типов
ячеек.Хотя мы знаем о многих генах, которые требуют для
процесса регенерации, мы до сих пор не знаем алгоритм, который достаточно , чтобы клетки знали, как строить или реконструировать сложные органы
к очень конкретной анатомической конечной цели. Таким образом, одна из главных опор будущего
работа в области биомедицины – это открытие процесса, с помощью которого крупномасштабные
анатомия определяется внутри коллективов клеток, и как мы можем это переписать
информация для рационального управления ростом и формой.Это также становится
ясно, что программное обеспечение жизни обладает многочисленными модулями или подпрограммами,
например «Построй глаз здесь», который можно активировать простым сигналом
триггеры. Обнаружение таких подпрограмм и
отображение логики развития – это новая область на пересечении
биология развития и информатика. Следующий важный шаг – попробовать
сформулировать вычислительные модели этого процесса, чтобы обогатить
концептуальный инструментарий биологов и помощь в переводе открытий
биологии в лучшую робототехнику и вычислительные технологии.
Представьте, если бы мы могли проектировать системы такой же пластичности и надежности, как
биологическая жизнь: структуры и машины, которые могут расти и ремонтироваться
сами себя. Такая технология трансформирует текущие усилия в
регенеративная медицина, где ученые и клиницисты стремятся открыть
входы или стимулы, которые могут заставить клетки тела строить структуры на
спрос по мере необходимости. Чтобы помочь разгадать загадку морфогенетического кода, и
также использовать знания биологии для создания самовосстанавливающихся систем в
в реальной жизни, мы пытаемся воспроизвести некоторые из желаемых свойств в in silico эксперимент.
Модель
Специалисты по инженерным дисциплинам и исследователи часто используют разные виды моделирование, включающее локальное взаимодействие, в том числе системы частичных производное уравнение (PDE), системы частиц и различные типы сотовых Автоматы (СА). Мы сосредоточимся на моделях клеточных автоматов в качестве дорожной карты для усилия по выявлению правил на уровне ячейки, которые приводят к сложным, регенеративное поведение коллектива. Центры сертификации обычно состоят из сетки ячейки, которые итеративно обновляются, с тем же набором правил, применяемых к каждая ячейка на каждом шагу.Новое состояние ячейки зависит только от состояний из нескольких ячеек в непосредственной близости. Несмотря на их очевидные простота, центры сертификации часто демонстрируют богатое, интересное поведение и долгая история применения для моделирования биологических явлений.
Давайте попробуем разработать правило обновления клеточного автомата, которое, начиная с одиночная ячейка, создаст предопределенный многоклеточный узор на 2D-сетке. Это наша аналогичная игрушечная модель развития организма.Чтобы спроектировать CA, мы должны указать возможные состояния ячеек и их функцию обновления. Типичный Модели CA представляют состояния ячеек с набором дискретных значений, хотя существуют варианты, использующие векторы непрерывных значений. Использование непрерывного values имеет то достоинство, что позволяет правилу обновления быть дифференцируемым функция состояний соседства ячейки. Правила, которыми руководствуются поведение отдельной клетки, основанное на локальной среде, аналогично низкоуровневая аппаратная спецификация, кодируемая геномом организма.Запуск нашей модели на заданное количество шагов от начальной конфигурации покажет поведение паттерна, которое обеспечивается таким оборудованием.
Итак – что же такого особенного в дифференцируемых правилах обновления? Они позволят
использовать мощный язык функций потерь, чтобы выразить свои пожелания, и
обширный существующий механизм вокруг градиентных числовых
оптимизация для их выполнения.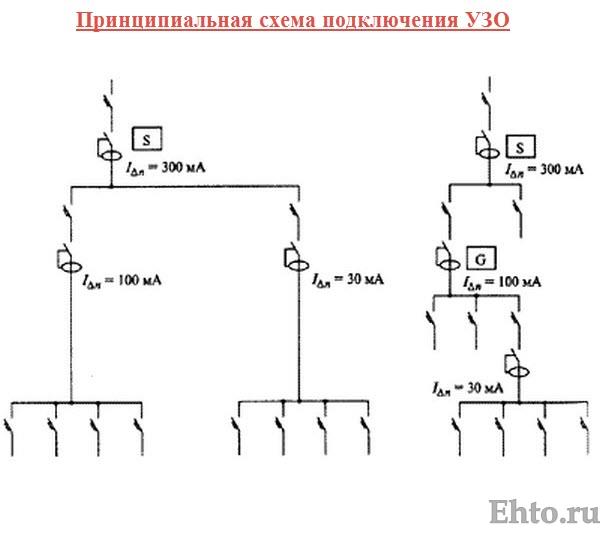 Искусство складывать отличные друг от друга
функции, и оптимизация их параметров для выполнения различных задач имеет
долгая история.В последние годы он процветал под разными названиями, такими как
(Глубокие) нейронные сети, глубокое обучение или дифференцируемое программирование.
Искусство складывать отличные друг от друга
функции, и оптимизация их параметров для выполнения различных задач имеет
долгая история.В последние годы он процветал под разными названиями, такими как
(Глубокие) нейронные сети, глубокое обучение или дифференцируемое программирование.
Состояние ячейки
Мы представим состояние каждой ячейки как вектор из 16 реальных значений (см. рисунок выше). Первые три канала представляют цвет ячейки, видимый для нас (RGB). Целевой шаблон имеет значения цветового канала в диапазоне [0,0,1,0] [0,0, 1,0] [0,0,1,0]. и α \ alphaα равным 1.0 для пикселей переднего плана и 0,0 для фона.
Альфа-канал (α \ alphaα) имеет особое значение: он разграничивает живые клетки, принадлежащие выращиваемому образцу. В частности, клетки имеющие α> 0,1 \ alpha> 0,1α> 0,1 и их соседи считаются «живыми». Другой ячейки являются «мертвыми» или пустыми, и для них явно заданы значения вектора состояния до 0,0 на каждом временном шаге. Таким образом, клетки с α> 0,1 \ alpha> 0,1α> 0,1 можно рассматривать как как «зрелые», а их соседи с α≤0.1 \ alpha \ leq 0.1α≤0.1 «растут», а могут стать зрелыми, если их альфа превышает порог 0,1.
state⃗ → 0.00 \ vec {state} \ rightarrow 0.00state⃗ → 0.00, когда нет соседа с α> 0.10 \ alpha> 0.10α> 0.10 Скрытые каналы не имеют предопределенного значения, и это зависит от обновления.
правило, чтобы решить, для чего их использовать. Их можно интерпретировать как
концентрации некоторых химикатов, электрические потенциалы или другие
сигнальный механизм, который используется клетками для управления ростом.В
с точки зрения нашей биологической аналогии – все наши клетки имеют один и тот же геном
(правило обновления) и различаются только информацией, закодированной
химические сигналы, которые они получают, излучают и хранят внутри (их состояние
векторы).
Правило клеточного автомата
Пришло время определить правило обновления. Наш CA работает на обычной 2D-сетке из 16-мерные векторы, по сути, трехмерный массив формы [высота, ширина, 16]. Мы хотим применить одну и ту же операцию к каждой ячейке, и результат этого операция может зависеть только от небольшой (3×3) окрестности ячейки.Этот сильно напоминает операцию свертки, один из краеугольных камней обработки сигналов и дифференциального программирования. Свертка – это линейная операции, но ее можно комбинировать с другими операциями для каждой ячейки для получения сложное правило обновления, способное запомнить желаемое поведение. Наша ячейка Правило обновления можно разделить на следующие этапы, применяемые по порядку:
Восприятие. Этот шаг определяет, что каждая клетка воспринимает. окружающая среда.Мы реализуем это с помощью свертки 3×3 с фиксированное ядро. Кто-то может возразить, что определение этого ядра излишне – в конце концов, мы могли бы просто заставить клетку научиться необходимому восприятию коэффициенты ядра. Наш выбор фиксированных операций мотивирован тот факт, что реальные клетки часто полагаются только на химические градиенты, чтобы направлять развитие организма. Таким образом, мы используем классические фильтры Собеля для оценки частные производные каналов состояний клеток в x⃗ \ vec {x} x⃗ и y⃗ \ vec {y} y⃗ направлений, формируя двумерный вектор градиента в каждом направлении, для каждый государственный канал.Мы объединяем эти градиенты с собственными ячейками. состояний, образуя 16 * 2 + 16 = 4816 * 2 + 16 = 4816 * 2 + 16 = 48 мерный вектор восприятия , или скорее воспринимаемых векторов, по на каждую ячейку.
по умолчанию (state_grid):
sobel_x = [[-1, 0, +1],
[-2, 0, +2],
[-1, 0, +1]]
sobel_y = транспонировать (sobel_x)
# Свернутые фильтры Собеля с состояниями
# по x, y и размеру канала.
grad_x = conv2d (sobel_x, state_grid)
grad_y = conv2d (sobel_y, state_grid)
# Объединить каналы состояния ячейки,
# градиенты каналов по x и
# градиент каналов по y.
perception_grid = concat (
state_grid, grad_x, grad_y, axis = 2)
вернуть perception_grid
Правило обновления. Каждая ячейка теперь применяет серию операций к вектору восприятия, состоящему из типичного дифференцируемого программирования строительные блоки, такие как 1×1-свертки и нелинейности ReLU, которые мы вызовите “правило обновления” ячейки.Напомним, что правило обновления изучено, но в каждой ячейке выполняется одно и то же правило обновления. Сеть, параметризующая это обновление Правило состоит примерно из 8000 параметров. Вдохновленный остаточной нервной системой сети, правило обновления выводит инкрементное обновление состояния ячейки, который применялся к ячейке до следующего временного шага. Правило обновления разработан, чтобы демонстрировать начальное поведение «ничего не делать» – реализовано инициализация весов последнего сверточного слоя в правиле обновления с нуля.Мы также не применяем ReLU к выходу последнего слоя правило обновления, поскольку инкрементные обновления состояния ячейки должны обязательно уметь как прибавлять, так и убавлять из состояния.
обновление по умолчанию (perception_vector):
# Следующий псевдокод работает на
# вектор восприятия отдельной клетки.
# В нашей эталонной реализации используется 1D
# сверток по соображениям производительности.
x = плотный (perception_vector, output_len = 128)
x = relu (x)
ds = плотный (x, output_len = 16, weights_init = 0.0)
возврат ds
Обновление стохастической ячейки. Типичное обновление клеточного автомата все клетки одновременно. Это подразумевает наличие глобальных часов, синхронизация всех ячеек. Не стоит полагаться на глобальную синхронизацию можно ожидать от самоорганизующейся системы. Мы ослабляем это требование, предполагая, что каждая ячейка выполняет обновление независимо, ожидая случайный интервал времени между обновлениями. Чтобы смоделировать это поведение, мы применяем случайная маска для каждой ячейки для обновления векторов, установка всех значений обновления на ноль с некоторой предопределенной вероятностью (мы используем 0.5 во время тренировки). Этот Операцию можно также рассматривать как применение отсева для каждой ячейки для обновления векторов.
def stochastic_update (state_grid, ds_grid):
# Обнулить случайную часть обновлений.
rand_mask = cast (random (64, 64) <0,5, float32)
ds_grid = ds_grid * rand_mask
вернуть state_grid + ds_grid
Маскировка живых клеток. Мы хотим смоделировать процесс роста который начинается с одной ячейки и не хочет, чтобы пустые ячейки участвовали в вычислений или несут какое-либо скрытое состояние.Мы обеспечиваем это явным обнуление всех каналов пустых ячеек. Ячейка считается пустой, если в его окрестности 3×3 нет «зрелой» (альфа> 0,1) клетки.
по умолчанию alive_masking (state_grid):
# Возьмем альфа-канал как мерило «жизни».
в живых = max_pool (state_grid [:,:, 3], (3,3))> 0,1
state_grid = state_grid * cast (жив, float32)
вернуть state_grid
Эксперимент 1. Учимся расти
Тренировочный режим для обучения целевому паттерну.В нашем первом эксперименте мы просто обучаем CA для достижения целевого изображения. после случайного количества обновлений. Этот подход довольно наивен и будет работать в вопросы. Но проблемы, с которыми он сталкивается, помогут нам улучшить будущее. попытки.
Мы инициализируем сетку нулями, кроме одной исходной ячейки в центре, в котором будут все каналы, кроме RGB Мы устанавливаем RGB-каналы начального числа на ноль, потому что хотим, чтобы он был видимым. на белом фоне.установлен на единицу. После инициализации сетки мы итеративно применяем обновление. правило. Мы выбираем случайное количество шагов CA из [64, 96] Это должно быть достаточное количество шагов, чтобы вырастить узор размер, с которым мы работаем (40×40), даже с учетом стохастической природы наших обновить правило. диапазон для каждого шага обучения, так как мы хотим, чтобы шаблон был стабильным на протяжении количество итераций. На последнем шаге мы применяем пиксельную потерю L2 между Каналы RGBA в сетке и целевом шаблоне.Эта потеря может быть дифференцированно оптимизированный Мы наблюдали тренировочную нестабильность, которая проявлялась в виде резкие скачки величины потерь на более поздних этапах обучения. Мы удалось смягчить их, применив нормализацию L2 для каждой переменной к градиенты параметров. Это может иметь эффект, похожий на вес нормализация. Другое обучение параметры доступны в сопроводительном исходном коде. в отношении параметров правила обновления путем обратного распространения во времени, стандартный метод обучения рекуррентных нейронных сетей.
Как только оптимизация сойдется, мы можем запустить моделирование, чтобы увидеть, как наши изученные паттерны роста CA, начиная с семенной клетки. Посмотрим, что происходит, когда мы выполняем его дольше, чем количество шагов, использованных во время подготовка. На анимации ниже показано поведение нескольких разных моделей. обучены генерировать различные шаблоны эмодзи.
Ваш браузер не поддерживает видео тег. Многие модели демонстрируют нестабильность в течение более длительных периодов времени.Воспроизвести в записной книжке
Мы видим, что различные обучающие прогоны могут привести к созданию моделей с очень большим различное долгосрочное поведение. Некоторые имеют тенденцию вымирать, некоторые, кажется, не умирают. знаю, как перестать расти, но некоторые оказываются почти стабильными! Как мы можем направить обучение на постоянное создание устойчивых паттернов?
Эксперимент 2: То, что сохраняется, существует
Один из способов понять, почему предыдущий эксперимент был нестабильным, – это нарисовать параллель динамическим системам.Мы можем рассматривать каждую клетку как динамическая система, в которой каждая ячейка разделяет одну и ту же динамику, и все ячейки будучи локально связанными между собой. Когда мы обучаем нашу клетку обновлению модель мы корректируем эту динамику. Наша цель – найти динамику, которая удовлетворяют ряду свойств. Изначально мы хотели, чтобы система развивалась. от исходного образца к целевому образцу – траектория, которую мы достигли в эксперименте 1. Теперь мы хотим избежать наблюдаемой нестабильности, которая в нашей метафоре динамической системы состоит в том, чтобы сделать целевой шаблон аттрактор.
Одна из стратегий для достижения этого – позволить CA выполнять итерацию в течение гораздо более длительного времени. и периодически прикладывая урон к цели, тренируя систему путем обратного распространения через эти более длительные интервалы времени. Интуитивно мы утверждаем что с более длинными временными интервалами и несколькими приложениями потерь модель с большей вероятностью создаст аттрактор для целевой формы, поскольку мы итеративно формировать динамику, чтобы вернуться к целевому паттерну из любого места система решила рискнуть.Однако более длительные периоды времени существенно увеличить время тренировки и, что более важно, память требования, учитывая, что промежуточные активации всего эпизода должны быть сохраненным в памяти для выполнения обратного прохода.
Вместо этого мы предлагаем стратегию, основанную на «пуле образцов», для достижения аналогичного эффекта. Мы определить пул начальных состояний для запуска итераций, изначально заполненных с начальным состоянием одиночного черного пикселя. Затем мы пробуем партию из этого бассейн, который мы используем на нашем этапе обучения.Чтобы предотвратить эквивалент «Катастрофическое забывание» заменяем один образец в этой партии на исходное однопиксельное начальное состояние. По завершении этапа обучения мы заменить образцы в пуле, которые были отобраны для партии, выходными состояния из шага обучения над этой партией. На анимации ниже показан случайная выборка записей в пуле каждые 20 шагов обучения.
определение pool_training ():
# Установить альфа и скрытый каналы на (1.0).
семя = нули (64, 64, 16)
начальное число [64 // 2, 64 // 2, 3:] = 1.0
target = цели [«ящерица»]
пул = [начальное число] * 1024
для i в диапазоне (training_iterations):
idxs, партия = pool.sample (32)
# Сортировать по убыванию, по убыванию.
партия = sort_desc (партия, потеря (партия))
# Замените образец с наибольшими потерями семенем.
партия [0] = начальное число
# Провести обучение.
выходов, потери = поезд (партия, цель)
# Поместите выходы обратно в пул.
пул [idxs] = выводит
Ваш браузер не поддерживает видео тег. Случайная выборка паттернов в пуле во время обучения, отобранная каждые 20 тренировочных шагов.Воспроизвести в записной книжке
На ранних этапах тренировочного процесса случайная динамика в системе позволяет модель попадет в различные неполные и неправильные состояния.Как эти состояния выбираются из пула, мы уточняем динамику, чтобы иметь возможность оправиться от таких состояний. Наконец, по мере того, как модель становится более надежной из начального состояния в целевое состояние, образцы в пуле отражают это и с большей вероятностью будут очень близки к целевому паттерну, что позволяет обучение для дальнейшего совершенствования этих почти завершенных моделей.
По сути, мы используем предыдущие конечные состояния как новые отправные точки для заставляют наш CA научиться сохранять или даже улучшать уже сформированный шаблон, в дополнение к возможности вырастить его из семени.Это делает это можно добавить периодический убыток для значительно более длительных интервалов времени чем это возможно в противном случае, поощрение генерации аттрактора в качестве форма цели в нашей связанной системе. Мы также заметили, что пересев выборка с наибольшими потерями в пакете вместо случайной делает обучение более стабильный на начальных этапах, так как помогает убирать некачественные состояния из пула.
Вот как выглядит типичный прогресс обучения правилу CA.Клетка Правило учится стабилизировать паттерн параллельно с уточнением его характеристик.
Ваш браузер не поддерживает видео тег. Поведение CA на шагах обучения 100, 500, 1000, 4000.Воспроизвести в записной книжке
Эксперимент 3: Обучение регенерации
Помимо способности выращивать собственное тело, живые существа отлично их поддерживает. Мало того, что изношенная кожа заменяется новой кожа, но очень тяжелые повреждения сложных жизненно важных органов могут быть восстановлены в некоторые виды.Есть ли вероятность, что некоторые из моделей, которые мы обучили выше есть регенеративные способности?
Ваш браузер не поддерживает видео тег. При повреждении узоры проявляют некоторые регенерирующие свойства, но не полный повторный рост.Воспроизвести в записной книжке
На приведенной выше анимации показаны три разные модели, обученные с использованием одного и того же настройки. Мы позволяем каждой из моделей развить шаблон более 100 шагов, затем повредить конечное состояние пятью разными способами: удаляя разные половинки сформированного узора, и вырезав из центра квадрат.Один раз опять же, мы видим, что эти модели показывают совсем другой режим вне тренировки. поведение. Например, «ящерица» развивает довольно сильную регенеративную способность. возможности, без явного обучения этому!
Поскольку мы обучили нашу связанную систему ячеек генерировать аттрактор к целевой форме из одной ячейки, вероятно, что эти системы, после повреждения будет обобщаться в сторону несаморазрушающих реакций. Это потому, что системы были обучены расти, стабилизироваться и никогда не полностью самоуничтожиться.Некоторые из этих систем могут естественным образом притягиваться к регенеративным способностям, но ничто не мешает им развиваться различное поведение, такое как взрывные митозы (неконтролируемый рост), невосприимчивость к повреждению (сверхстабилизация) или даже самоуничтожение, особенно для наиболее серьезных повреждений.
Если мы хотим, чтобы наша модель показывала более последовательные и точные регенеративные возможностей, мы можем попытаться увеличить область притяжения для нашей цели узор – увеличивают пространство конфигураций ячеек, которые естественным образом тяготеют к нашей целевой форме.Мы сделаем это, повредив несколько отобранных из пула состояния перед каждым шагом обучения. Теперь система должна быть способна регенерация из состояний, поврежденных случайно расположенными стирающими кругами. Наш надеюсь, что это будет распространено на регенерационные способности от различные виды повреждений.
Ваш браузер не поддерживает видео тег. Повреждение образцов в бассейне способствует изучению надежных восстановительные качества. Строка 1 – образцы из пула, Строка 2 – их соответствующие состояния после итерации модели.Воспроизвести в записной книжке
На приведенной выше анимации показан прогресс обучения, включая примерный урон. Мы отбираем 8 состояний из пула. Затем мы заменяем образец с наибольшими потерями (крайний левый верхний на рисунке выше) с исходным состоянием и повредить три состояния с наименьшими потерями (верхний правый угол) путем установки случайной круговой области в шаблоне до нулей. В нижней строке показаны состояния после итерации. из соответствующего самого верхнего начального состояния. Как и в эксперименте 2, результирующие состояния возвращаются в пул.
Ваш браузер не поддерживает видео тег. Узоры, подверженные повреждениям во время тренировок, демонстрируют поразительные регенеративные возможности.Воспроизвести в записной книжке
Как видно из приведенной выше анимации, модели, подвергшиеся повреждениям во время тренировок гораздо более устойчивы, в том числе к видам повреждений не опытных в тренировочном процессе (например, прямоугольные повреждения как над).
Эксперимент 4. Вращение поля восприятия
Как описано ранее, мы моделируем восприятие клеткой соседних ячеек путем оценки градиентов каналов состояний в x⃗ \ vec {x} x⃗ и y⃗ \ vec {y} y⃗ с использованием фильтров Собеля.Удобная аналогия: у каждого агента есть два датчика (например, хемосенсорные рецепторы), указывающие ортогонально направления, которые могут ощущать градиенты в концентрации определенных химикаты вдоль оси датчика. Что произойдет, если мы повернем эти датчики? Мы можем сделать это, вращая ядра Собеля.
[KxKy] = [cosθ − sinθsinθcosθ] ∗ [SobelxSobely] \ begin {bmatrix} K_x \\ K_y \ end {bmatrix} = \ begin {bmatrix} \ cos \ theta & – \ sin \ theta \\ \ sin \ theta & \ cos \ theta \ end {bmatrix} * \ begin {bmatrix} Sobel_x \\ Sobel_y \ end {bmatrix} [Kx Ky] = [cosθsinθ −sinθcosθ] ∗ [Sobelx Sobely]Эта простая модификация поля восприятия дает повернутые версии. шаблона для угла выбора без переобучения, как показано ниже.
Вращение оси, по которой шаг восприятия вычисляет градиенты вызывает повернутые версии узора.Воспроизвести в записной книжке
В идеальном мире, не квантованном отдельными ячейками в пиксельной решетке, это было бы неудивительно, ведь в конце концов, можно было бы ожидать воспринимаемые градиенты в x⃗ \ vec {x} x⃗ и y⃗ \ vec {y} y⃗ инвариантны к выбранному угол – простая смена системы отсчета. Однако важно обратите внимание, что в модели на основе пикселей все не так просто.Вращающийся пиксель основанная на графике включает в себя вычисление сопоставления, которое не обязательно является биективным и обычно включает интерполяцию между пикселями для достижения желаемого результат. Это потому, что один пиксель при повороте теперь, скорее всего, будет перекрывают несколько пикселей. Успешный рост моделей, как указано выше, предполагает определенная устойчивость к основным условиям за пределами тех испытал во время обучения.
CA и PDE
Существует обширная литература, описывающая различные ароматизаторы клеточных автоматов и систем PDE и их приложения для моделирование физических, биологических или даже социальных систем.Хотя было бы невозможно дать краткий обзор этой области в нескольких строках, мы будем опишите несколько ярких примеров, вдохновивших на эту работу. Алан Тьюринг представил свои знаменитые паттерны Тьюринга еще в 1952 году. , предлагая, как системы реакции-диффузии могут быть действительной моделью для химического поведения во время морфогенеза. Особенно вдохновляющая модель реакции-диффузии, которая выдержала испытание временем – модель Грея-Скотта , который показывает крайнее разнообразие поведение контролируется всего несколькими переменными.
С тех пор, как фон Нейман представил центры сертификации как модели для самовоспроизведения они захватили умы исследователей, которые наблюдали чрезвычайно сложные поведение, возникающее из очень простых правил. Точно так же более широкая аудитория вне академических кругов были соблазнены жизненным поведением CA благодаря Игра жизни Конвея. Возможно частично мотивировано доказательством того, что такая простая вещь, как Правило 110, Тьюринг завершен, книга Вольфрама « Новый вид науки» требует сдвига парадигмы в центре внимания вокруг широкого использования элементарных компьютерных программ, таких как CA как инструменты для познания мира.
Совсем недавно несколько исследователей обобщили “Игру жизни” Конвея на работу. на более непрерывных доменах. Нас особенно вдохновили работы Рафлера SmoothLife и Ления из Чана , последний из который также обнаруживает и классифицирует целые виды «форм жизни».
Ряд исследователей использовали эволюционные алгоритмы для поиска правил CA. которые воспроизводят предопределенные простые шаблоны . Например, Дж. Миллер предложил эксперимент, аналогичный нашему, с использованием эволюционных алгоритмов для разработки CA Правило, которое могло построить и возродить французский флаг, начиная с семени клетка.
Нейронные сети и самоорганизация
Тесная связь между сверточными нейронными сетями и сотовой Автоматы уже наблюдались рядом исследователей. . В связь настолько сильна, что позволила нам построить нейронные модели CA, используя компоненты, легко доступные в популярных фреймворках машинного обучения. Таким образом, используя другой жаргон, наш Neural CA потенциально может быть назван «Recurrent Остаточные сверточные сети с выпадением «на пиксель».
Нейронный графический процессор предложения вычислительная архитектура очень похожа на нашу, но применяется в контекст обучения умножению и алгоритм сортировки.
Если смотреть шире, мы думаем, что концепция самоорганизации находит свое отражение в массовом машинном обучении с популяризацией Графические модели нейронных сетей. Обычно GNN выполняет повторное вычисление по вершинам (возможно, динамический) график. Вершины сообщаются локально через ребра графа, и агрегировать глобальную информацию, необходимую для выполнения задачи по нескольким раундов обмена сообщениями, так же как атомы можно рассматривать как общаются друг с другом, чтобы создать новые свойства молекула или даже точки точки облако разговаривает со своими соседями, чтобы выяснить их глобальную форму .
Самоорганизация также проявилась в увлекательной современной работе с использованием большего количества традиционные сети динамических графов, в которых авторы развили Самособирающиеся агенты для решения множества виртуальных задач .
Swarm Robotics
Одна из самых ярких демонстраций силы самоорганизации. когда это применяется к моделированию роя. Еще в 1987 году Рейнольдс Боидс смоделировал стайку птиц с просто крошечный набор правил, созданных вручную.В настоящее время мы можем встраивать крошечных роботов с программами и проверять их коллективное поведение на физических агентах, как продемонстрировано такими работами, как Mergeable Nervous Systems и килоботы . Насколько нам известно, программы встроенные в роевые роботы в настоящее время разрабатываются людьми. Мы надеемся, что наш работа может служить источником вдохновения для данной области и способствовать созданию коллективное поведение посредством дифференцируемого моделирования.
Обсуждение
Эмбриогенетическое моделирование
Ваш браузер не поддерживает видео тег.Способный к регенерации двухголовый планарий, создание, которое вдохновило этот работуВоспроизвести в записной книжке
В этой статье описывается игрушечная модель эмбриогенеза и регенерации. Это основное направление для будущей работы со многими приложениями в биологии и вне. В дополнение к значениям для понимания эволюции и контроль регенерации и использование этого понимания для биомедицинских ремонт, есть биоинженерия.При переходе поля от синтетическая биология коллективов отдельных клеток до истинной синтетической морфологии новых живых машин, это будет иметь важное значение для разработки стратегий программирования на системном уровне. возможности, такие как анатомический гомеостаз (регенеративная репарация). Она имеет давно известно, что регенеративные организмы могут восстанавливать специфические анатомический узор; однако совсем недавно было обнаружено, что цель морфология не жестко закодирована ДНК, но поддерживается физиологический контур, который хранит уставку для этого анатомического гомеостаза .Техники теперь доступно для перезаписи этой уставки, в результате чего, например, у двухголовых плоских червей что при разрезании на части в простой воде (без дополнительных манипуляций) приводят к появлению последующих поколений регенерированных двухголовых червей (как показано над). Важно приступить к разработке моделей вычислительной процессы, которые хранят целевое состояние системного уровня для поведения роя , чтобы можно было разработать эффективные стратегии для рационального редактирования этого информационная структура, приводящая к желаемым крупномасштабным результатам (таким образом, победить обратную проблему, которая сдерживает регенеративную медицину и многие другие другие достижения).
Инженерия и машинное обучение
Модели, описанные в этой статье, работают на мощном графическом процессоре современного компьютер или смартфон. Но давайте порассуждаем о том, что «более физически» реализация такой системы могла бы выглядеть. Мы можем представить это как сетку крошечных независимых компьютеров, имитирующих отдельные ячейки. Каждый из тех компьютерам потребуется примерно 10 КБ ПЗУ для хранения «ячейки геном »: веса нейронной сети и управляющий код, а также около 256 байт RAM для состояния ячейки и промежуточных активаций.Клетки должны иметь возможность для передачи своих 16-значных векторов состояния соседям. Каждая ячейка также требуется RGB-диод для отображения цвета пикселя, который он представляет. А обновление одной ячейки потребует около 10 тыс. операций умножения-сложения и выполняет не нужно синхронизировать по сети. Мы предполагаем, что клетки могут ждать случайных интервалов времени между обновлениями. Система, описанная выше единообразно и децентрализовано. Тем не менее, наш метод позволяет его запрограммировать. для достижения предопределенного глобального состояния и восстановления этого состояния в случае многоэлементные сбои и перезапуски.Поэтому мы предполагаем такой вид моделирование можно использовать для создания надежных самоорганизующихся агентов. На более теоретический фронт машинного обучения, мы показываем пример децентрализованная модель, способная выполнять чрезвычайно сложные задачи. Мы верим это направление должно быть противоположным более традиционному используемому глобальному моделированию. в большинстве современных работ в области глубокого обучения, и мы надеемся эта работа послужит источником вдохновения для изучения более децентрализованного обучения моделирование.
Эта статья является частью Тема для дифференцируемых самоорганизующихся систем, экспериментальный формат сбора приглашенных коротких статей, углубляющихся в дифференцируемые самоорганизующиеся системы с вкраплениями критических комментарии нескольких экспертов в смежных областях.
Тема для дифференцируемых самоорганизующихся систем Самоклассифицирующиеся цифры MNIST«Моделирование топологических эффектов на динамику клеточными автоматами» Адвайта Апте, Джона В. Кейна и др.
Название журнала / книги / конференции
Журнал биологической инженерии
Аннотация
Фон
Мотивы прямого распространения – важные функциональные модули в биологических и других сложных сетях. Функциональность мотивов с прямой связью и других сетевых мотивов в значительной степени продиктована связностью отдельных сетевых компонентов. В то время как исследования динамики мотивов и сетей обычно посвящены временному или пространственному описанию процессов, это исследование фокусируется на взаимосвязи между конкретной архитектурой и общей скоростью процессов семейства мотивов с прямой связью, включая двойные и двойные. тройные петли с прямой связью.Поиск наиболее эффективной сетевой архитектуры может представлять особый интерес для регуляторных или сигнальных путей в биологии, а также в вычислительных и коммуникационных системах.
Результаты
Динамика мотивов с прямой связью изучалась с использованием клеточных автоматов и сравнивалась с моделированием дифференциальным уравнением. Количество итераций клеточного автомата, необходимое для 100% превращения субстрата в целевой продукт, использовалось как обратная мера скорости трансформации.Было идентифицировано несколько основных топологических паттернов, которые упорядочивают определенные конструкции с прямой связью в соответствии со скоростью, которую они обеспечивают. При одинаковом количестве сетевых узлов и постоянных других параметрах, двухпараллельные и трехпараллельные мотивы обеспечивают более высокую эффективность сети, чем одиночные мотивы с прямой связью. Кроме того, топологическое свойство изодинамичности было идентифицировано для мотивов с прямой связью, где разные сетевые архитектуры приводили к одинаковой общей скорости целевого производства.
Заключение
Было показано, что для классов структурных мотивов с упреждающей архитектурой топология сети влияет на общую скорость процесса количественно предсказуемым образом. Эти фундаментальные результаты могут быть использованы в качестве основы для моделирования более крупных сетей как комбинаций более мелких сетевых модулей с последствиями для изучения синтетических генных цепей, небольших регуляторных систем и, в конечном итоге, динамических моделей целых клеток.
Права
© 2008 Apte et al; лицензиат BioMed Central Ltd.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа правильно процитировано.
Принципы дифференциальной защиты, которые вы ДОЛЖНЫ понимать
Дифференциальная защита
Хотя в настоящее время дифференциальная защита достигается численно, для понимания принципов дифференциальной защиты полезно проанализировать повсеместное электромеханическое реле.
Принципы дифференциальной защиты, которые вы ДОЛЖНЫ понимать (на фото: реле защиты SIPROTEC)На рисунке 1 показана простая схема дифференциальной защиты, также известная как схема Merz-Price .
В этой простой схеме мы можем предположить, что при нормальных условиях эксплуатации ток, входящий в часть оборудования под защитой , равен (или, в случае трансформатора, пропорционален) его выходному току. В этом примере мы предположим, что входной и выходной токи равны.Автоматический выключатель с каждой стороны защищаемого оборудования управляется реле максимального тока.
Рисунок 1 – Простая дифференциальная защита (щелкните, чтобы развернуть схему)Трансформаторы тока одинакового типа и коэффициента трансформации устанавливаются с обеих сторон оборудования. Эти трансформаторы тока индуцируют идентичные вторичные токи, потому что их первичные токи идентичны и у них одинаковое отношение витков.
Путем простого осмотра схемы становится ясно, что в этих условиях ток утечки не будет протекать через реле , поэтому сигналы отключения генерироваться не будут.
… и при возникновении неисправности
Рассмотрим неисправность , внутреннюю для оборудования . Через короткое замыкание будет протекать большой ток, поэтому ток, выходящий из оборудования, быстро уменьшится, что приведет к уменьшению вторичного тока в CT B . Это вызовет протекание тока через реле, величина которого будет достаточной для отключения автоматических выключателей.
Теперь рассмотрим внешний отказ в F , как показано на рисунке 2.
Рисунок 2 – Простая дифференциальная защита с внешним отказомВы можете видеть, что в этом случае ток на выходе из оборудования, хотя и большой, все еще такой же, как ток на входе в него, поэтому реле не сработает. Это именно то, что мы хотим. , потому что внешние по отношению к оборудованию неисправности находятся в другой зоне защиты и защищены другой схемой.
Если защищаемое оборудование представляет собой, например, шину или обмотку генератора, очевидно, что выходной ток такой же, как и входной.Если, однако, оборудование представляет собой трансформатор, у которого коэффициент трансформации не равен единице, то входящий ток будет отличаться от выходящего тока.
В этом случае трансформаторы тока должны быть сбалансированы с эквивалентным дифференциалом передаточного числа.
Дифференциальная схема создает четко определенную зону защиты, охватывающую все, что находится между двумя трансформаторами тока . Любая неисправность, существующая в этой зоне защиты, рассматривается как внутренняя неисправность, а любая неисправность, существующая за пределами этой зоны защиты, является внешней неисправностью.
Следовательно, дифференциальная схема должна быть способна реагировать на самые маленькие внутренние неисправности, но ограничивать самые большие внешние неисправности.
На практике, этого трудно достичь – особенно при очень больших сквозных КЗ из-за неидеальности трансформаторов тока, используемых для измерения токов. Термин, используемый для обозначения способности системы справляться с этими недостатками, называется Устойчивость при отказе .
В современных IED (интеллектуальных электронных устройствах) ток в трансформаторах тока не контролирует напрямую рабочую катушку, которая отключает выключатели, поэтому подключение не такое, как показано в этом примере.На самом деле токи от трансформаторов тока просто вводятся в IED, где они дискретизируются и оцифровываются.
Дифференциальный режим затем выполняется программным обеспечением IED.
Основная дифференциальная теория трансформатора (ВИДЕО)
Ссылка // Принципы автоматизации подстанции Майкла Дж.

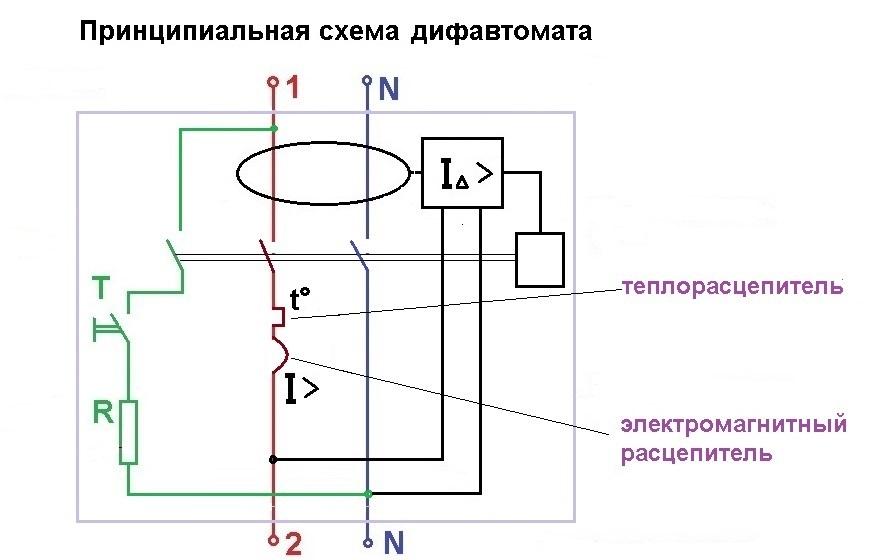


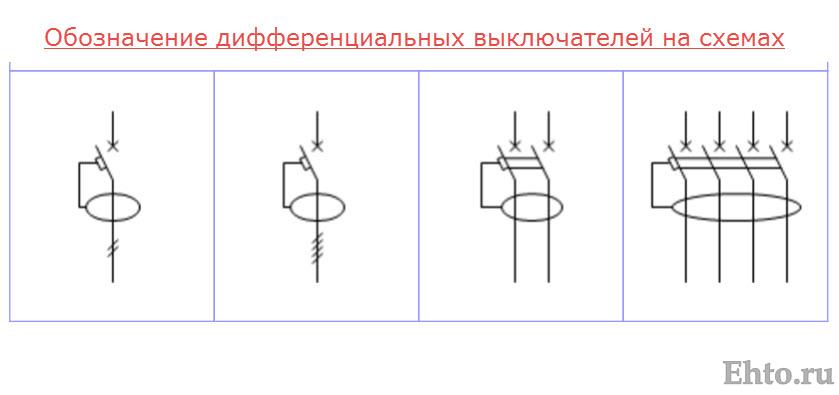 На эффективность его работы такое положение не повлияет, главное, не перепутать клеммы подключения.
На эффективность его работы такое положение не повлияет, главное, не перепутать клеммы подключения.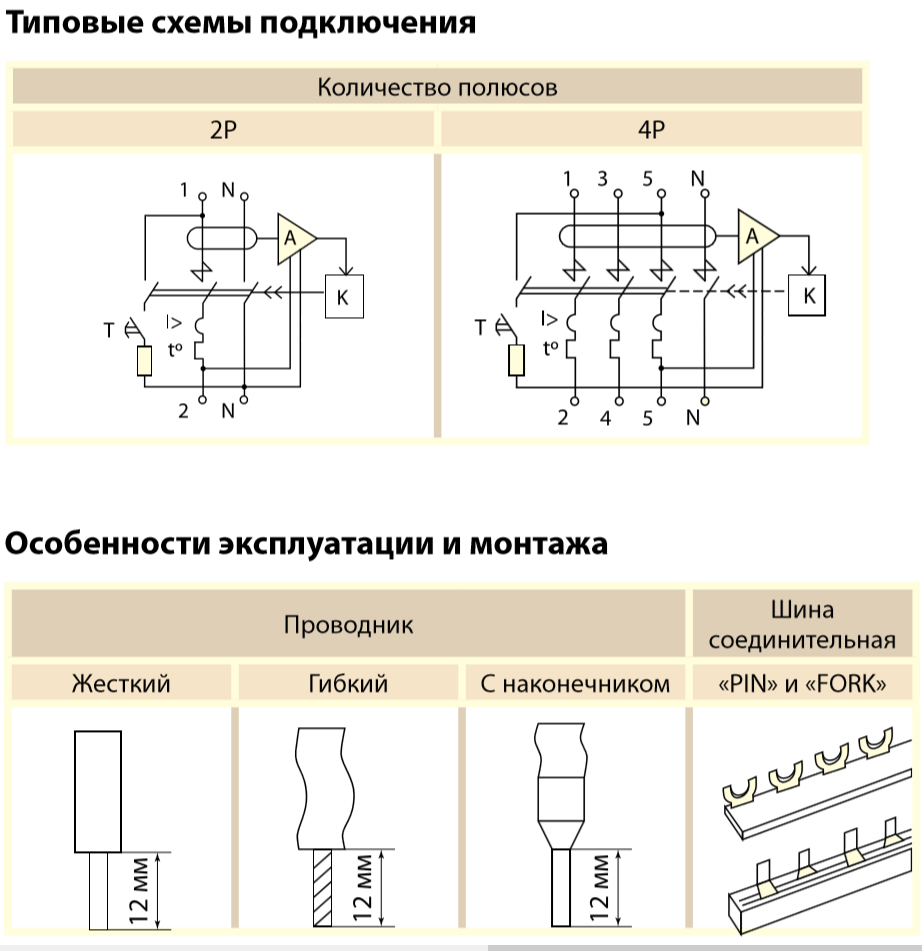
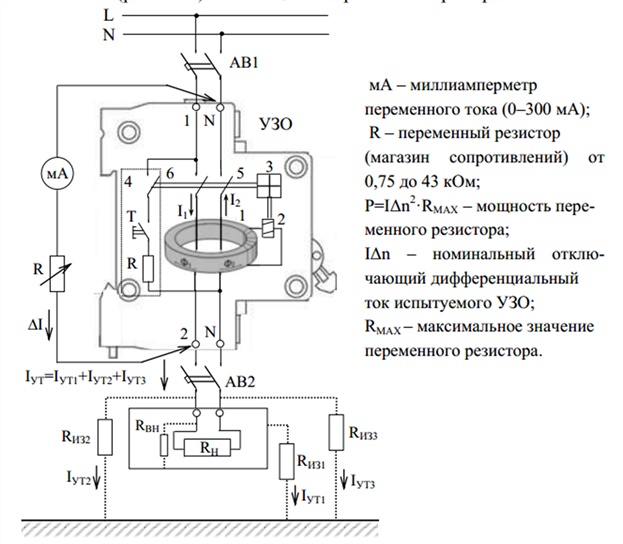 Выбор сечения определяется номиналом. Схема нанесена на корпус.
Выбор сечения определяется номиналом. Схема нанесена на корпус. Вскоре он начал думать о робототехнике и, возможно, представил, как реализовать пример с использованием игрушечного конструктора. Однако по аналогии с электронными схемами он понял, что 2D должно быть достаточно. И следуя предложению 1951 года Станислава Улама (который, возможно, уже независимо рассматривал проблему), он упростил свою модель и получил двумерный клеточный автомат (он, очевидно, надеялся позже преобразовать результаты обратно в дифференциальные уравнения).Конкретный клеточный автомат, который он построил в 1952-1953 годах, имел 29 возможных цветов для каждой ячейки и сложные правила, специально разработанные для имитации работы компонентов электронного компьютера и различных механических устройств. Чтобы дать математическое доказательство возможности самовоспроизведения, фон Нейман затем обрисовал в общих чертах построение конфигурации из 200 000 клеток, которые будут воспроизводить себя (детали были заполнены Артуром Берксом в начале 1960-х). Фон Нейман, по-видимому, полагал – предположительно отчасти из-за сложности реальных биологических организмов и электронных компьютеров – что нечто подобное этому уровню сложности неизбежно будет необходимо для системы, чтобы демонстрировать сложные возможности, такие как самовоспроизведение.В этой книге я показываю, что это абсолютно не так, но с интуицией, которую он получил из существующей математики и инженерии, фон Нейман, по-видимому, никогда не мог себе этого представить.
Вскоре он начал думать о робототехнике и, возможно, представил, как реализовать пример с использованием игрушечного конструктора. Однако по аналогии с электронными схемами он понял, что 2D должно быть достаточно. И следуя предложению 1951 года Станислава Улама (который, возможно, уже независимо рассматривал проблему), он упростил свою модель и получил двумерный клеточный автомат (он, очевидно, надеялся позже преобразовать результаты обратно в дифференциальные уравнения).Конкретный клеточный автомат, который он построил в 1952-1953 годах, имел 29 возможных цветов для каждой ячейки и сложные правила, специально разработанные для имитации работы компонентов электронного компьютера и различных механических устройств. Чтобы дать математическое доказательство возможности самовоспроизведения, фон Нейман затем обрисовал в общих чертах построение конфигурации из 200 000 клеток, которые будут воспроизводить себя (детали были заполнены Артуром Берксом в начале 1960-х). Фон Нейман, по-видимому, полагал – предположительно отчасти из-за сложности реальных биологических организмов и электронных компьютеров – что нечто подобное этому уровню сложности неизбежно будет необходимо для системы, чтобы демонстрировать сложные возможности, такие как самовоспроизведение.В этой книге я показываю, что это абсолютно не так, но с интуицией, которую он получил из существующей математики и инженерии, фон Нейман, по-видимому, никогда не мог себе этого представить.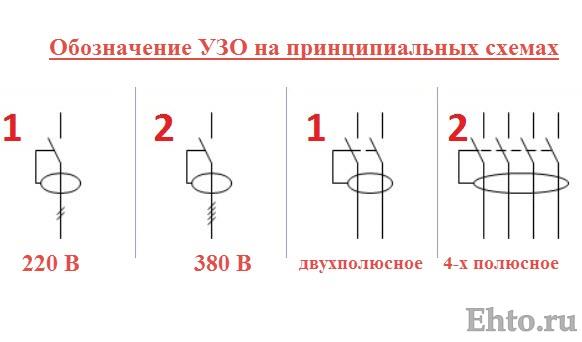 Начиная с начала 1960-х годов были замечены несколько довольно простых общих черт клеточных автоматов, которые, как считалось, имеют отношение к самовоспроизведению, и изучались с использованием все более сложного технического формализма. (Примером был результат так называемого Эдемского сада, согласно которому в клеточных автоматах могут быть конфигурации, которые возникают только как начальные условия; см. Стр. 963.Также были сделаны различные явные конструкции клеточных автоматов, поведение которых проявляло определенные простые особенности, возможно, относящиеся к самовоспроизведению (такие как так называемая синхронизация расстрельной команды, как на странице 1039).
Начиная с начала 1960-х годов были замечены несколько довольно простых общих черт клеточных автоматов, которые, как считалось, имеют отношение к самовоспроизведению, и изучались с использованием все более сложного технического формализма. (Примером был результат так называемого Эдемского сада, согласно которому в клеточных автоматах могут быть конфигурации, которые возникают только как начальные условия; см. Стр. 963.Также были сделаны различные явные конструкции клеточных автоматов, поведение которых проявляло определенные простые особенности, возможно, относящиеся к самовоспроизведению (такие как так называемая синхронизация расстрельной команды, как на странице 1039).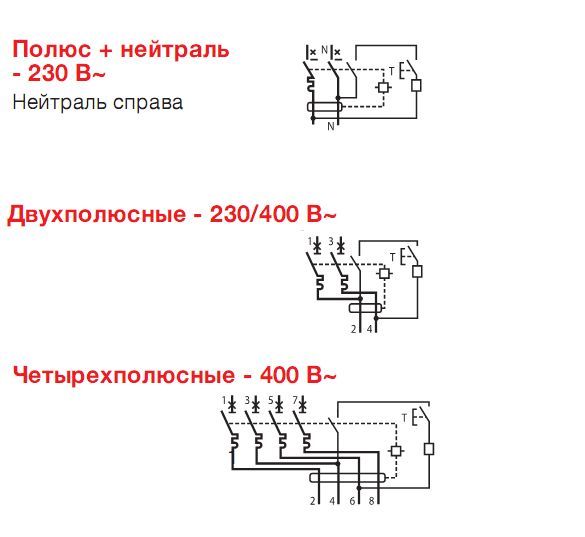 Однако примерно в 1960 году было проведено несколько симуляций, связанных с двумерными клеточными автоматами. Станислав Улам и другие использовали компьютеры в Лос-Аламосе для создания нескольких примеров того, что они называли рекурсивно заданными геометрическими объектами – по сути, результатов развития обобщенных двумерных клеточных автоматов из отдельных черных ячеек (см. Стр. 930).Особенно после получения больших изображений в 1967 году Улам отметил, что по крайней мере в одном случае довольно простые правила роста порождают сложную структуру, и упомянул, что это может иметь отношение к биологии. Но, возможно, из-за того, что традиционные математические методы почти не продвинулись в этом направлении, результат не был широко известен и никогда не использовался. (Улам попытался построить одномерный аналог, но в итоге получил не клеточный автомат, а вместо этого последовательности, основанные на числах, обсуждаемых на странице 910.Примерно в 1961 году Эдвард Фредкин смоделировал двумерный аналог правила 90 на компьютере PDP-1 и отметил его свойства самовоспроизведения (см. Стр. 1186), но в целом его больше интересовало обнаружение простых физических свойств.
Однако примерно в 1960 году было проведено несколько симуляций, связанных с двумерными клеточными автоматами. Станислав Улам и другие использовали компьютеры в Лос-Аламосе для создания нескольких примеров того, что они называли рекурсивно заданными геометрическими объектами – по сути, результатов развития обобщенных двумерных клеточных автоматов из отдельных черных ячеек (см. Стр. 930).Особенно после получения больших изображений в 1967 году Улам отметил, что по крайней мере в одном случае довольно простые правила роста порождают сложную структуру, и упомянул, что это может иметь отношение к биологии. Но, возможно, из-за того, что традиционные математические методы почти не продвинулись в этом направлении, результат не был широко известен и никогда не использовался. (Улам попытался построить одномерный аналог, но в итоге получил не клеточный автомат, а вместо этого последовательности, основанные на числах, обсуждаемых на странице 910.Примерно в 1961 году Эдвард Фредкин смоделировал двумерный аналог правила 90 на компьютере PDP-1 и отметил его свойства самовоспроизведения (см. Стр. 1186), но в целом его больше интересовало обнаружение простых физических свойств. (В 1978 году Джонатан Миллен в качестве возможного одномерного аналога Жизни, который легче было реализовать на ранних персональных компьютерах, кратко рассмотрел то, что оказалось тотальным правилом кода 20 k = 2, r = 2 со страницы 283.)
(В 1978 году Джонатан Миллен в качестве возможного одномерного аналога Жизни, который легче было реализовать на ранних персональных компьютерах, кратко рассмотрел то, что оказалось тотальным правилом кода 20 k = 2, r = 2 со страницы 283.)
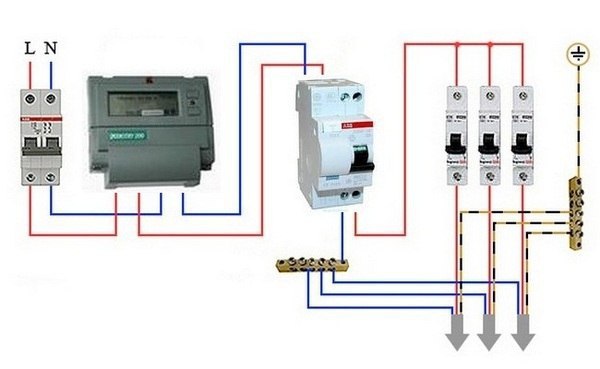 Стр. 963).В 1950-х и начале 1960-х годов в этой области (по крайней мере, в США) проводились работы ряда выдающихся чистых математиков, но, поскольку они были в значительной степени применимы к криптографии, большая часть их держалась в секрете. И то, что было опубликовано, было в основном абстрактными теоремами о функциях, слишком глобальных, чтобы раскрыть какую-либо сложность, о которой я говорю.
Стр. 963).В 1950-х и начале 1960-х годов в этой области (по крайней мере, в США) проводились работы ряда выдающихся чистых математиков, но, поскольку они были в значительной степени применимы к криптографии, большая часть их держалась в секрете. И то, что было опубликовано, было в основном абстрактными теоремами о функциях, слишком глобальных, чтобы раскрыть какую-либо сложность, о которой я говорю.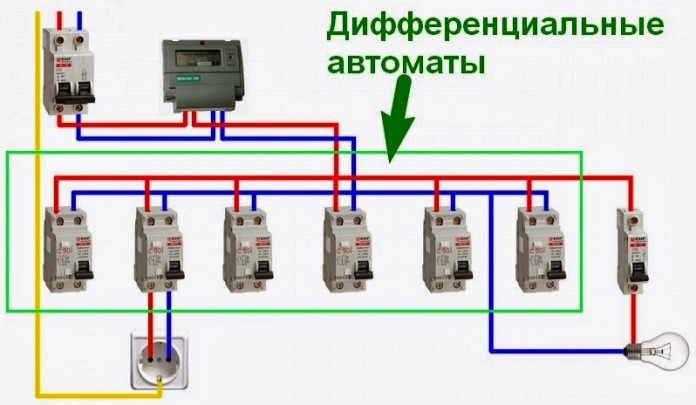 Публикация моей первой статьи о клеточных автоматах в 1983 г. (см. Стр. 881) привела к быстрому росту интереса к этой области, и с тех пор с тех пор количество статей постоянно увеличивалось (о чем свидетельствует количество исходных документов в Указанный ниже индекс научного цитирования) были опубликованы по клеточным автоматам – почти все они следуют указанным мною направлениям.
Публикация моей первой статьи о клеточных автоматах в 1983 г. (см. Стр. 881) привела к быстрому росту интереса к этой области, и с тех пор с тех пор количество статей постоянно увеличивалось (о чем свидетельствует количество исходных документов в Указанный ниже индекс научного цитирования) были опубликованы по клеточным автоматам – почти все они следуют указанным мною направлениям.