3 Схемы замещения трансформаторов – СтудИзба

Лекция 3.  Схемы замещения трансформаторов

На ПС применяют двух, трехобмоточные трансформаторы, а также АТ.

1) Двухобмоточный трансформатор условно обозначается так:

Первичная обмотка со вторичной имеет только магнитную связь.

Имеет две обмотки и связывает сети двух напряжений.

2) Трехобмоточный трансформатор связывает сети 3-х напряжений, и обозначается:

3) Двухобмоточный трансформатор с расщепленной обмоткой НН. U_нн1=U_нн2: U_нн1^>_<U_нн2 – 6,10кВ обозначается:

Рекомендуемые файлы

Трансформаторы выполняются либо трехфазными, либо однофазными (три однофазных трансформатора на ПС составляют одну трехфазную трансформаторную группу).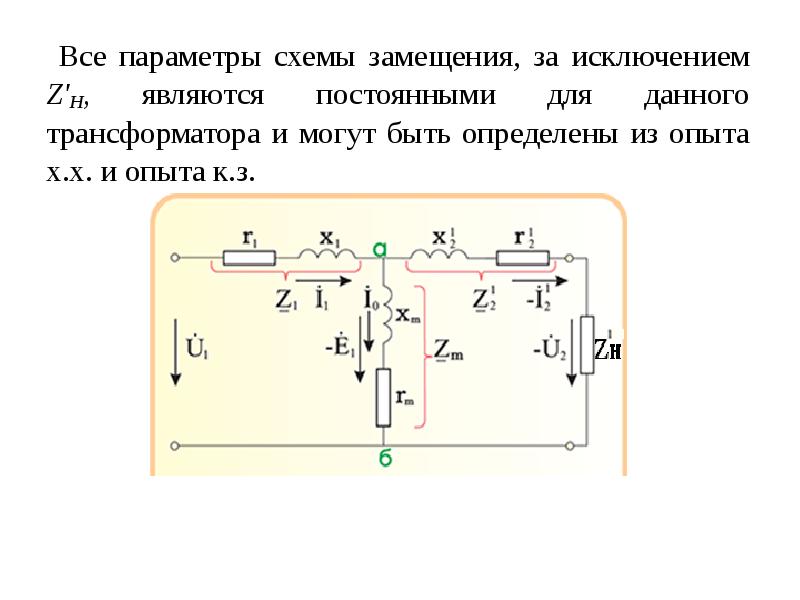

Двухобмоточный трансформатор

Влияние трансформаторов на режим работы системы учитывается с помощью схемы замещения (Г-образной). Такая схема замещения (Г-образная) для одной фазы двухобмоточного трансформатора показана на рис.1,

где r_Т=r₁+r^I₂ – сумма активного сопротивления первичной обмотки и приведенного к ней (к первичной) активного сопротивления вторичной обмотки;

х_Т=х₁+х^I₂ – сумма индуктивного сопротивления рассеяния первичной обмотки и приведенного к ней (к первичной) индуктивного сопротивления вторичной обмотки.

r_Т и х_Тназывают активным и индуктивным сопротивлениями трансформатора.

Проводимости g_Т и в_Т, определяют активную и реактивную слагающие намагничивающего тока трансформатора I_m.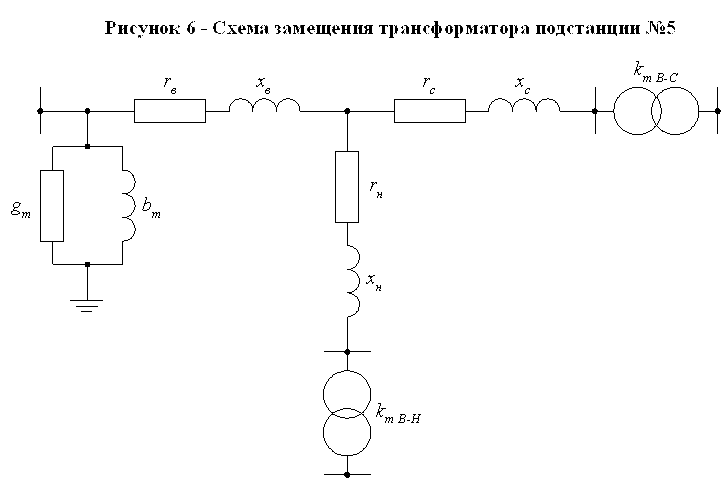

Активная составляющая этого тока обусловлена потерями мощности в стали трансформатора, а реактивная определяет магнитный поток взаимоиндукции обмоток трансформатора.

В схему включен идеальный трансформатор, не имеющий сопротивлений и магнитных потоков рассеяния. Соотношение напряжений на его зажимах постоянно и определяется коэффициентом трансформации реального трансформатора в режиме холостого хода.

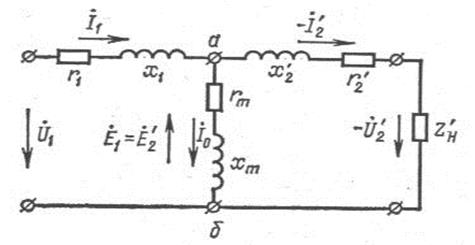
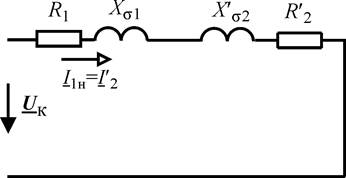
Обычно идеальный трансформатор в схемах замещения опускается, и расчеты выполняются к приведенным величинам вторичного напряжения U^I₂ и тока I^I₂ (см. рис.2 упрощенная схема замещения).

При U£220кВ ветви намагничивания учитываются в виде дополнительной нагрузки потери мощности в стали трансформатора или потери холостого хода.

где DР_хх+jDQ_хх – потери мощности в стали или потери х. х.

Опыт холостого хода

Проводимости ветви намагничивания определяются результатами опыта х.х. В этом опыте размыкается вторичная обмотка, а к первичной подводится номинальное напряжение. Ток в продольной части схемы замещения равен нулю, а к поперечной приложено Uном. Трансформатор потребляет в этом режиме только мощность, равную потерям холостого хода.

 

Как следует из схемы замещения, ток и мощность, потребляемая трансформатором в этом режиме, определяется параметрами цепи намагничивания

DR_хх»U²_ном´g_Т

DQ_xx»U²_ном´в_Т, откуда

g_Т=;    в_Т=.

Намагничивающая мощность DQ_хх обычно принимается равной полной мощности х. х. трансформатора S_хх в виду малости потерь активной мощности DR_хх в сравнении с DQ_хх.

DQ_хх»S_хх»I_m или I_xx

Мощность S_хх в относительных единицах равна току холостого хода в процентах, который указывается в каталожных данных.

I_m=

Проводимости g_Т и в_Т схемы замещения трансформатора определяются по результатам опыта х.х., в котором при разомкнутой вторичной обмотке к первичной обмотке трансформатора подводиться номинальное напряжение.

Для каждого трансформатора известны следующие параметры (каталожные данные) к ним относятся:

                       Потери  к.з.  DР_к.з., [кВт];

                       Потери  х.х.  DР_хх, [кВт];

                       Напряжение  короткого замыкания U_к, %;

                       Ток  холостого хода   I_xx=I_m, %.

Они позволяют определить все сопротивления и проводимости схемы замещения и вычислить потери активной и реактивной мощности в нем (стр.64 Идельчик).

Опыт короткого замыкания

Активное и индуктивное сопротивление одной фазы трансформатора может быть экспериментально определены из опыта короткого замыкания (к.з.). Этот опыт состоит в том, что вторичная обмотка трансформатора замыкается накоротко, а к первичной подводится такое напряжение, при котором токи в обеих обмотках трансформатора имеют номинальное значение. Это напряжение называется напряжением короткого замыкания (U_к).

 

Активная мощность, потребляемая трансформатором в опыте к.з., целиком расходуется на нагрев его обмоток. Потери в стали при этом ничтожны из-за малости приложенного напряжения (U_к£U_ном).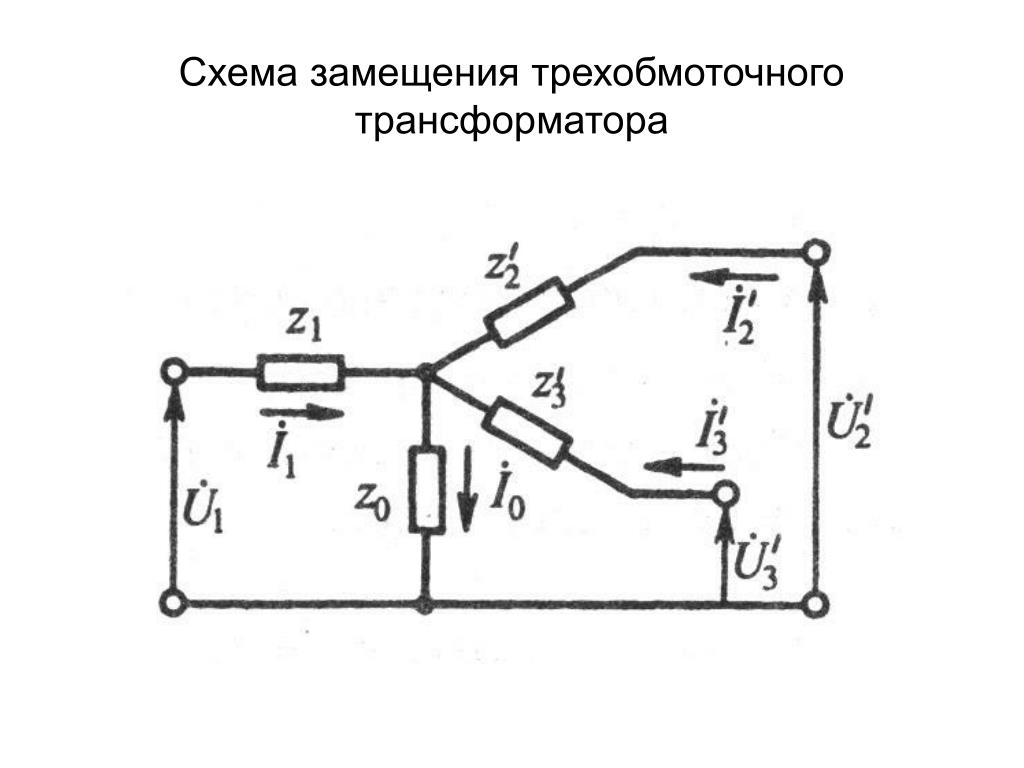 Поэтому можно считать, что в опыте к.з.:

DR_кз=3I²_номr_Т=;    S=´U´I;     I=;

откуда

Напряжение короткого замыкания (U_к) складывается из двух составляющих: Первая составляющая – падение напряжения в активном и вторая составляющая – в индуктивном сопротивлениях от тока, протекающего в режиме к.з. В крупных трансформаторах r_Т<<x_Т.

Пренебрегая падением напряжения в активном сопротивлении можно считать:

U_к%»U_r%=;       U_ф=;

откуда  х_Т=;

х_Т=

х_Т – в Ом, при U_ном – кВ, S_ном – МВА.

Передача мощности через трансформаторы сопровождается потерями мощности в активном и реактивном сопротивлениях его обмоток, а также с потерями связанными с намагничиванием стали.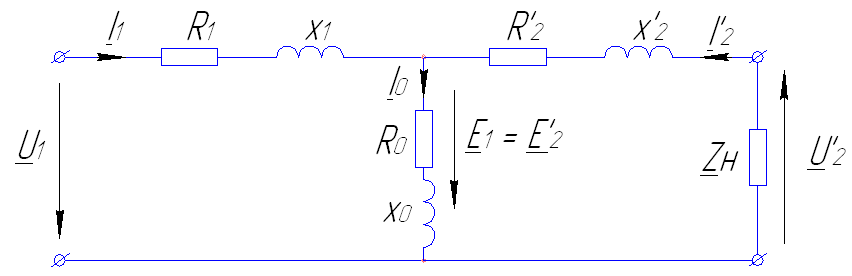

Потери, возникающие в обмотках, зависят от протекающего по ним тока; потери, идущие на намагничивание, определяются приложенным напряжением и в первом приближении может быть приняты неизменными и равными потерям х.х.

Суммарные потери мощности в трансформаторе:

DР_Т=3I²₂r_Т+DР_хх=

DQ_Т=3I²₂x_Т+DQ_xx=

DQ_xx – выразить через каталожные данные.

Когда напряжение U₂ неизвестно, принимают U₂=U_ном, к которому приведены сопротивления r_Т и х_Т.

При êêработе “n” одинаковых трансформаторов их эквивалентное сопротивление уменьшается ¯ в “n” раз, тогда как потери на намагничивание увеличиваются ­ в “n” раз.

При этом:                               DР_Т»

DQ_Т»

Потери мощности могут быть найдены по каталожным параметрам трансформаторов без предварительного вычисления сопротивлений r_Т и х_Т.

Поскольку потери к.з. DR_кз определяются при номинальном токе трансформатора.

DR_кз=3I²_ном´r_Т,

а при любом другом токе потери активной мощности в обмотках:(потери в меди)

DR_м=3I²₂´r_Т,

то справедлива зависимость:

Тогда при одном трансформаторе из (*) при известной реальной загрузке трансформаторов получим:                       DR_м=DR_кз´

При ççработе “n” одинаковых трансформаторов:  DR_Т=

Подставив выражение для реактивного сопротивления (5) в (7) получим:

DQ_Т=:(12)

Трехобмоточный трансформатор

Условное обозначение:

Имеет три обмотки, связывает сети трех напряжений.

Обмотки между собой имеют электромагнитную связь.

Схема замещения трехобмоточного трансформатора:

 

Схему замещения можно отобразить в упрощенном виде, где идеальные трансформаторы отсутствуют и сопротивления представлены в виде комплексных значений:

где r₁, r₂, r₃ – активные сопротивления трех обмоток трансформатора, приведенные к напряжению первичной обмотки;

х₁, х₂, х₃ – условные индуктивности рассеяния обмоток, также приведенные к напряжению первичной обмотки.

Параметры цепи намагничивания 3-х обмоточных трансформаторов определяется аналогично двухобмоточным.

Если в опытах к.з. при замыкании одной обмотки и отсутствии нагрузки у другой, замерить напряжение к.з. U_к(1-2), U_к(1-3), U_к(2-3) и потери мощности, то по формулам, полученным выше, можно определить суммарные сопротивления двух последовательно включенных лучей схемы замещения 3-х обмоточного трансформатора. При замыкании накоротко обмотки 2 и включения трансформатора под напряжение через обмотку 1 можно найти:

r₁₂=r₁+r₂=

x₁₂=x₁+x₂=

Другие опыты к.з. позволяют аналогично определить суммарные сопротивления:

(15)

Из систем уравнений (14) и (15) следует, что:

Значения напряжений к.з. U_к(1-2), U_к(1-3), U_к(2-3) нормированы и приводятся в каталожных данных.

Значение потерь к.з. дается в таблицах. В первом случае активные сопротивления обмоток могут быть найдены в предположении, что эти сопротивления приведены к одной ступени трансформации, обратно пропорциональны номинальным мощностям соответствующих обмоток, и отвечающие наибольшим потерям мощности. Приводятся три значения потерь:  DR_кз(1-2), DR_кз(1-3), DR_кз(2-3).

При определении активных и индуктивных сопротивлений обмоток, следует принять во внимание их исполнение.

Трехобмоточные  тр-ры имеют несколько исполнений. В одном из них каждая из обмоток тр-ра рассчитана на номинальную мощность. Есть возможность по любым двум обмоткам при отключенной третьей передавать полную номинальную мощность.

Соотношение мощностей обмоток у такого тр-ра 100/100/100%

Есть исполнение у новых трансформаторов, где соотношение мощностей  100/50/50%

                                                                                                                                        100/67/33%

                                                                                                                                        100/33/67%

50% или 67% или 33% соответствуют загрузке соответствующих обмоток на 50 или 67 или 33% от номинальной мощности тр-ра.

Выбор исполнения трехобмоточного тр-ра зависит от соотношения между мощностями нагрузок, питающихся от различных обмоток тр-ра.

При исполнении тр-ров с соотношением мощностей обмоток 100/100/100% все его активные сопротивления (приведенные) равны: r₁=r₂=r₃=

что следует из (13) при r₁=r₂.

Для тр-ров с соотношением мощностей обмоток 100/100/66,7 сопротивление первых двух обмоток определяется соотношением (17) сопротивление же третьей находиться из соотношения:     

При известных трех значениях потерь к.з. можно найти:

DR_кз1=

DR_кз2=

DR_кз3=

а затем с помощью формулы:  r_Т=; определить сопротивления r₁, r₂, r₃ по найденным значениям DR_кз1, DR_кз2, DR_кз3.

Потери реактивной и активной мощностей в 3-х обм. тр-рах можно вычислить суммированием потерь мощности в трех его обмотках; которые определяются по величине мощности, протекающей через соответствующую обмотку.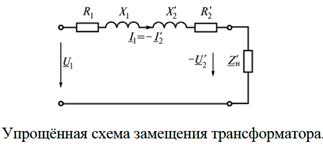

При неизвестных напряжениях в точках схемы замещения расчет ведется по номинальному напряжению, к которому приведены сопротивления обмоток.

Когда известны потери к.з. DR_кз1, DR_кз2, DR_кз3, потери активной мощности м.б. найдены приблизительно как:

DR_Т=

Здесь S₁, S₂, S₃ – нагрузки обмоток тр-ра.

Для потерь реактивной мощности при приблизительном расчете справедливо выражение:

DQ_Т=

(при выводе формул (18) и (19) принято, что потери мощности и напряжения к.з. приведены к номинальной мощности соответствующих обмоток).

Трансформатор с расщепленной обмоткой низшего напряжения

Соединяет ветви двух напряжений.

НАПРИМЕР: 110/10,5/10,5кВ или (110-ВН; 10,5-НН1; 10,5-НН2).

Соединяет сети ВН и двух ближайших (одного класса) напряжений.

НАПРИМЕР: 110/10,5/6,3кВ (110-ВН; 10,5-НН1; 6,3-НН2). 

Типы: ТРДН, ТРДЦН.

Мощность каждой обмотки низшего напряжения составляет часть номинальной мощности (1/2 S_ном). Допускается любое распределение нагрузки между ветвями расщепленной обмотки (одна ветвь может быть полностью нагружена, а вторая отключена или обе ветви нагружены полностью).

;                    ;

;

;

.

Схема замещения трансформатора с расщепленной обмоткой низшего напряжения.

 

Автотрансформаторы

Рис 1

Наряду с трансформаторами, для связи электрических сетей с различными напряжениями, широко применяются автотрансформаторы (АТ).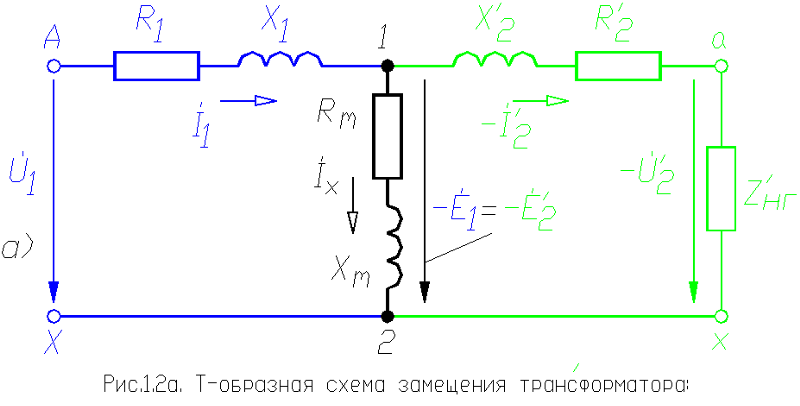

Условное обозначение АТ в схемах: (Рис. 1)

АТ осуществляют непосредственную электрическую связь между сетями высшего и среднего напряжения, обеспечивают перетоки мощности как односторонние, так и реверсивные, одновременно могут питать нагрузку на стороне НН или через присоединенные к обмотке НН, синхронные компенсаторы могут выдавать в сеть СН опережающего мощность и др. Наиболее характерным режимом АТ является выдача мощности из магистральных сетей ВН в сети СН для электроснабжения значительных районов.

Основное отличие АТ и Т заключается в следующем:

*                    в трансформаторе первичная обмотка со вторичной обмоткой имеет только магнитную связь;

·       в АТ между обмотками ОА ОС осуществляется электрическая связь

       Эл. связанные обмотки АО и СО. Часть обмотки между выводами АО называется последовательной, а между выводами СО называется общей.

       Последовательная и общая обмотки имеют между собой как магнитную, так и электрическую связь. Обмотка низкого напряжения с двумя другими обмотками имеет только магнитная связь.

       В АТ часть мощности передается непосредственно без трансформации, через контактную (электрическую) связь между последовательной и общей обмотками.

       Токораспределение у АТ другое. Если мощность передается с ВН®СН и с ВН®НН.

       В понижающем АТ ток в общей обмотке (I_тр) определяется разностью токов, замыкающихся через сети ВН и СН. Эта обмотка рассчитывается на ток меньший I_ном АТ, определяемого на стороне ВН.

       АТ в каждой фазе имеет обмотку ОА-ВН, состоящую из общей обмотки ОС-СН и последовательной обмотки АС. Эти обмотки соединены между собой по автотрансформаторной схеме, т.е. электрически. Третья обмотка – третичная НН всегда соединена треугольником и имеет трансформаторную электромагнитную связь с обмоткой ОА (ВН), т.е. с общей (ОС) и последовательной (АС), что на схеме отражено.

При работе АТ в режиме понижения напряжения в последовательной обмотке проходит ток I_в, который создавая магнитный поток, наводит в общей обмотке ток I₀. Ток нагрузки вторичной обмотки I_с складывается из тока I_в, проходящего благодаря гальванической (электрической) связи обмоток, и тока I₀, созданного магнитной связью этих обмоток:

  I_с= I_в+ I₀,   откуда I₀+ I_с– I_в.

 АТ также как и трансформатор характеризуются номинальными напряжениями и мощностью.

       Под номинальной мощностью АТ понимается предельная проходная мощность, которая может быть передана через АТ на стороне ВН:

S_ном = Ö3 I_в. U_в

Мощность, которую АТ может принять из сети ВН или передать в эту сеть, называется проходной мощностью S_прох, причем S_прох= S_тр,+ S_э,

S_тр – трансформаторная мощность;

S_э – электрическая мощность.

       Для характеристики АТ введено еще понятие типовой номинальной мощности S_т, на которую рассчитывается последовательная обмотка (АС).

       Типовая, т.е. трансформаторная  мощность АТ при номинальных условиях характеризует способность АТ передавать мощность магнитным путем. Она определяет габариты и стоимость АТ, а также расход материалов и мощность отдельных обмоток.

       Для этой последовательной обмотки, протекающая по ней мощность определяется при отсутствии нагрузки НН.

S_т=S_ном×a

 – коэффициент трансформации;

или =,    где a=1-;

a -коэффициент выгодности;

k – коэффициент трансформации.

       Т.о. типовая мощность характеризует мощность передаваемую электромагнитным путем, через обмотки, связанные электрически.

       При использовании третичной обмотки (НН) в понижающих АТ для питания нагрузки (или для присоединения к ней генератора в повышающих АТ) предельная ее мощность равна типовой.

В понижающем АТ при передаче мощности с ВН®СН и ВН®НН в общей обмотке ОС (СН) протекает разность токов Iв – Iс. Вследствие этого общая обмотка рассчитана на ток меньший номинального, и мощность этой обмотки равна его типовой мощности. (S_{общ.обм.}=S_тип.)

Т.о. конструкция понижающего АТ делает возможным передачу мощности больше той, на которую рассчитываются его обмотки. Понижающие АТ поэтому дешевле трех обмоточных трансформаторов той же мощности и характеризуются меньшим расходом активных материалов на их изготовление и следовательно меньшими потерями активной мощности.

Преимущества АТ проявляются в большей степени при малых значениях (коэффициент выгодности), т.е. тогда, когда они связывают сети более близких напряжений.

                                      S_т=S_ном×a;   .

       АТ, как и трех обмоточные трансформаторы характеризуются потерями и токами ХХ (DР_хх, I_m=I_хх) и тремя значениями напряжений КЗ.

       Таблицы параметров АТ содержат при значения потерь КЗ, отвечающие трем опытам КЗ. Причем одно из них DР_кз(в-с)= DР_кз(1-2) приводятся отнесенными к номинальной мощности АТ, а два других DР’_кз(в-н)= DР’_кз(1-3) и  DР’_кз(с-н)= DР’_кз(2-3) в ряде случаев указываются отнесенными к типовой мощности.

       Эта особенность отвечает условиям осуществления опытов КЗ. При КЗ обмотки НН, рассчитанной на типовую мощность, напряжение поднимается до величины, определяющей в этой обмотке ток, соответствующий типовой, а не номинальной мощности.

       При КЗ на стороне СН и подаче напряжения на ВН, это напряжение может подниматься до величины, при которой ток в последовательной обмотке достигнет значения, отвечающего номинальной мощности АТ.

       Для АТ справедлива схема замещения трехобмоточного трансформатора.

      

 

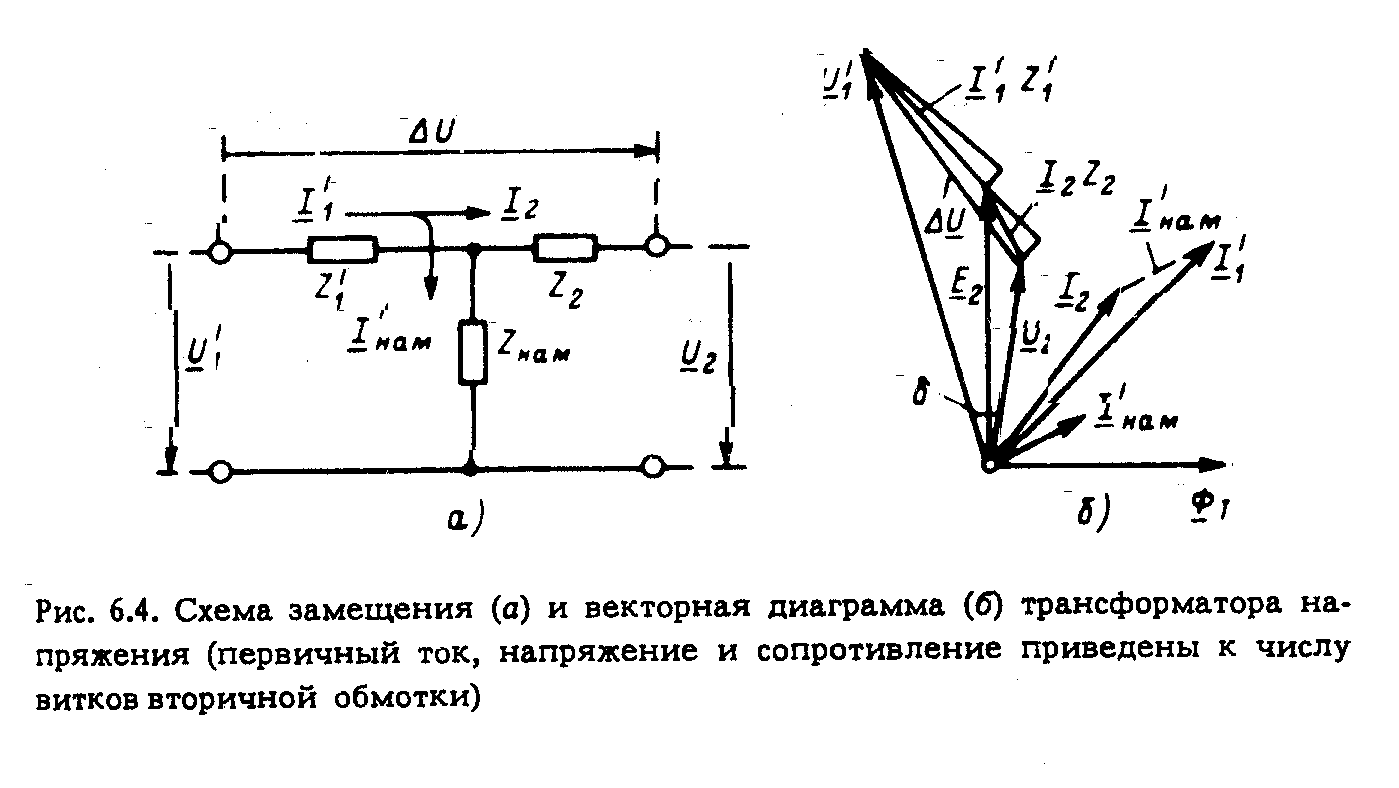
Параметры ветви намагничивания определяются по формулам:

;                .

Также как и для трансформаторов реактивные сопротивления могут быть найдены по выражениям:

; ;      .

После вычисления по формулам:

;

НО только после приведения всех табличных значений напряжений КЗ к одной номинальной мощности АТ.

  и.

       При определении активных сопротивлений все значения потерь КЗ (DР_КЗ) также должны быть приведены к номинальной мощности АТ:

    и   ;

Тогда

;  ; .

И аналогично выражениям для Х1, Х2, Х3:

;  ;  .

       Для вычисления потерь активной и реактивной мощностей в АТ можно выполнить расчет режима его схемы замещения. Можно также воспользоваться табличными значениями потерь КЗ (DР_КЗ) и напряжений КЗ (U_k%). В последнем случае искомые величины определяются формулами:

;

и

в которых табличные данные должны  подставляться приведенными к номинальной мощности АТ.

       Для снижения стоимости ПС и уменьшения потерь электроэнергии при трансформации в сетях напряжением 110кВ и выше применяют автотрансформаторы (АТ) вместо трех обмоточных (Т) трансформаторов. При применении автотрансформатора 220/110/10кВ удельная экономия меди (кг/кВ×А) составляет примерно 15-25%, а его полный вес в 1,5 раза меньше, чем трансформатора. Суммарные потери энергии уменьшаются на 30-35%.

Расчет режимов кольцевых сетей

На рисунке  а)  показана схема сети с несколькими нагрузками. Головные участки включены на шины питающего пункта А – это или системная п/ст или эл.станция. Если эту схему представить разрезанной по питающему пункту и развернутой, то она будет иметь вид линии с двусторонним питанием, у которой напряжения по концам равны по величине и фазе  ( рис.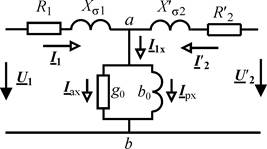 б )

На рисунке  в)  приведена расчетная схема этой сети:

Здесь S₁, S₂ , S₃ – расчетные нагрузки п/ст, включающие саму нагрузку узлов, зарядные мощности  0.5 линий и потери мощности в трансформаторах.

Направление потоков мощности на отдельных участках схемы принимается условно. Действительные направления определяются в результате расчета.

     Известными для расчета являются:

1.                    Напряжение в точке питания

2.                    Мощность нагрузок

Расчет должен выполняться методом последовательных приближений.

Первое приближение – равенство напряжений вдоль линии,это напряжение принимают равным номинальному напряжению линии.

Второе приближение  –  отсутствие потерь мощности.

При этих допущениях ,токи, протекающие по отдельным участкам схемы определяются соотношением:

                                                             

Условие равенства напряжений по концам линии означает равенство нулю падения напряжения в схеме.

Условие равенства нулю падения напряжения на основании 2^-го закона Кирхгофа может быть записано следующим образом:

                       

или ,если сократить во всех членах Ö3U_ном

                                      

Выразим входящие в это уравнение мощности участков II, III, IV через мощность S_I и известные мощности нагрузок  S₁, S₂, S₃:

                                                          

Откуда:                                            

                                                         

Кроме того, на основании 1^-го закона Кирхгофа имеем:

                                                              

                                                          

Подставив (2)-(5) в исходное уравнение (1):

                     

После преобразования получим:

       

                                 

                                       

                                         

откуда, c учетом обозначений рис. в) следует,что

Или   

Подставив формулы (2)-(5) в уравнение (1) для  S_IV после аналогичных преобразований получим:

Или    

В общем случае при  «n» нагрузках на кольцевой линии:

                                 и                  

где  Z_mA  и  Z_{mA– сопротивления  от точки  m , в которой включена промежуточная нагрузка  Sm до точки питания A и A соответственно.}

     После определения мощностей, протекающих по головным участкам сети, можно найти мощности на остальных участках с помощью закона Кирхгофа, последовательно примененного для каждой точки включения нагрузки. Определение потоков мощности является первым этапом расчета.

    На втором этапе определяются потери мощности, а также напряжения в узловых точках схемы.

Допустим , что в результате  I  этапа найдено распределение мощностей показанное на рис. а)

К точке 2 мощность поступает с двух сторон. Такая точка называется  точкой потокораздела. Обычно изображается зачерненным треугольником.

    Если исходную схему мысленно разрезать по точке потокораздела, то получим схему, изображенную на рисунке б).

    Такая операция не изменит распределение мощностей во всей сети в целом, если считать в точке 2 включенной нагрузку с потребляемой мощностью  S_II , а в точке 2 – нагрузку с мощностью  S_III.

Схема , изображенная на рисунке б), состоит из двух независимых частей, каждая из которых характеризует разомкнутую сеть с заданными нагрузками  S₁,S_II и S₃,S_III  и напряжениями

U_A = U_A на шинах источника питания. Дальнейший расчет осуществляется также как для разомкнутых сетей «по данным начала».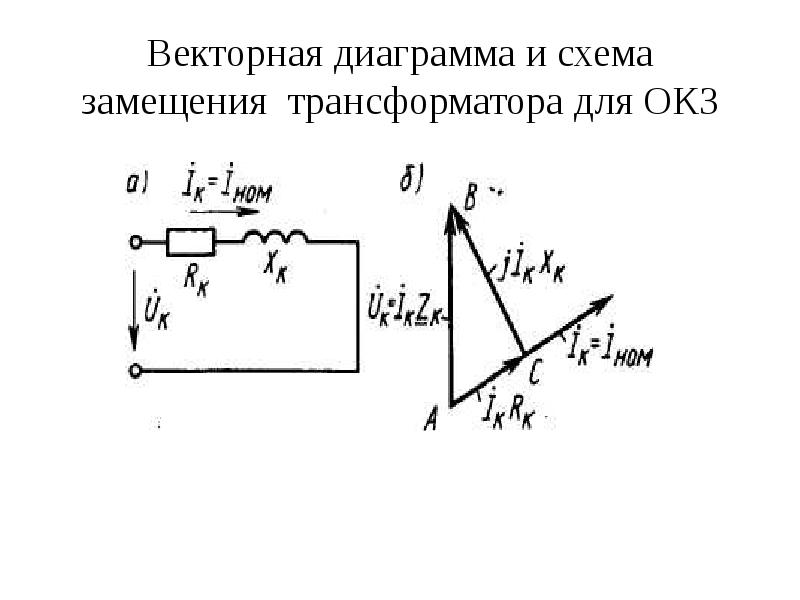 При этом, должны быть найдены уточненные значения мощностей, учитывающие потери мощности на участках схемы, начиная с концов

 при допущении, что  U = U_ном, а затем должны быть вычислены напряжения в узловых точках, начиная с точек  A и A .

     Иногда может выявиться две точки потокораздела – одна для активной, другая для реактивной мощности.

Такой случай иллюстрируется на рисунке 2, где точка 2 является точкой потокораздела для активной, а точка 3 – для реактивной мощности.
    Кольцевая сеть разделяется на две разомкнутые. Предварительно вычисляют потери мощности на участке между точками потокораздела:

                                             

                                           

Если принять, что в точке 2 включена нагрузка

                              

а в точке 3 нагрузка

                             

то можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на последнем рисунке.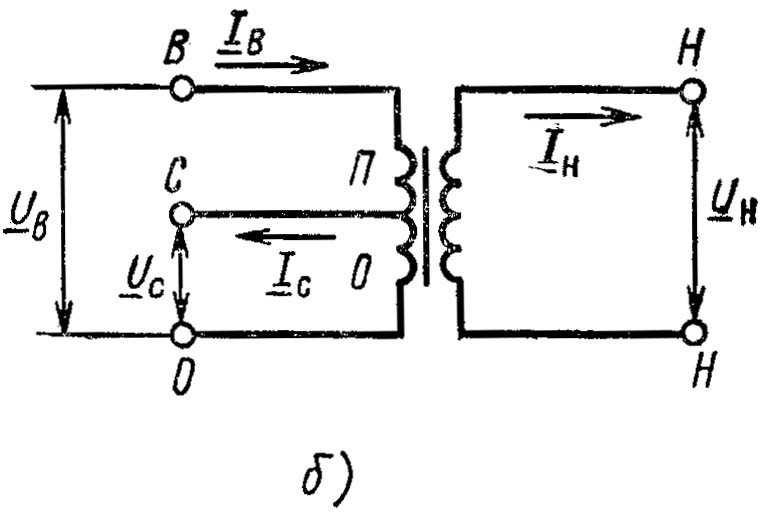

Совместный расчет режима сетей

нескольких номинальных напряжений

       В энергосистеме работают сети нескольких номинальных напряжений, связанных между собой трансформаторами и автотрансформаторами.

Схема сети.

Схема замещения.

       Рассмотрим особенности расчета режима в таких случаях.

       Идеальный трансформатор отражает наличие трансформации между цепями 110 и 35 кВ.

       При этом сопротивления трансформатора учитываются элементами  Z_тв2, Z_тс2 (Z_тн2  нет т.к. D S_тн2 вошли в S₂).

       В узловых точках 1, 0 и 3 включены расчетные нагрузки подстанций 1, 2 и 3 ().

       В составе S₁ кроме нагрузки потерь в трансформаторе учтены зарядные мощности половин линий Л1 и Л2, в S₂ учтена нагрузка узла и потери в обмотке Z_тн2 , в S₃ учтена нагрузка и потери в трансформаторе (зарядная мощность 1/2 линии ЛЧ  не учитывается, т.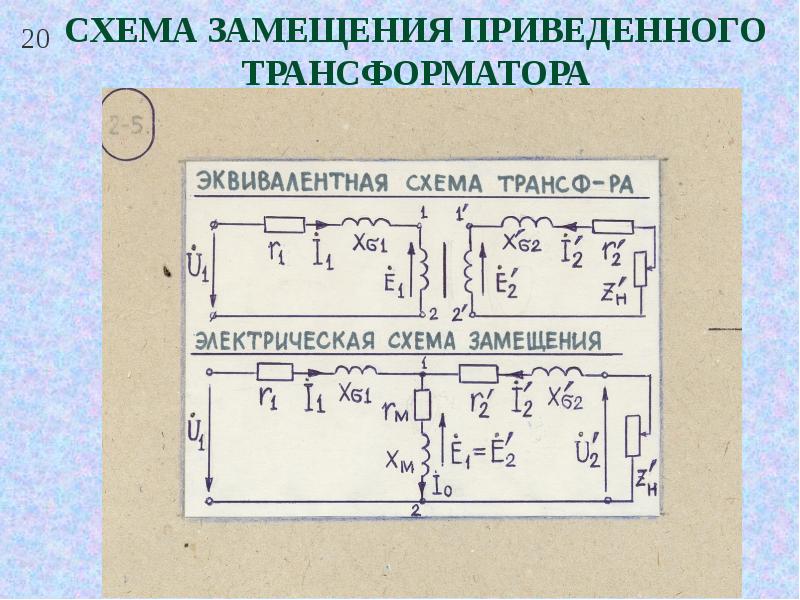 к. U=35кВ).

       Рассмотрим сначала последовательность расчета схемы «по данным конца». Расчет участка 3-2 выполняется аналогично приведенным ранее расчетам.

       Результатом расчета будет определение напряжения  и мощности . При коэффициенте трансформации k _tb-c, а мощность , т.к. трансформатор – идеальный и он не имеет сопротивлений.

       После определения и  расчет выполняется применительно к схеме одного номинального напряжения.

       Расчет «по данным начала» выполняется в два этапа, по аналогии с расчетом для сети с одним U_ном.

       На первом этапе определяется:

1.     потери мощности;

2.     значения мощностей во всех элементах схемы замещения, при условии, что напряжение во всех точках сети имеет номинальное значение.

Для линии ЛЧ U_ном=35кВ, для остальных элементов схемы U_ном=110кВ.

На втором этапе определяется во втором приближении:

1.      напряжения в узловых точках по заданному напряжению в точках питания А и найденных на первом этапе мощностям в начале каждого из элементов схемы.

       Затем при последовательном переходе от одной узловой точки питания А к концу линии ЛЧ определяется приведенное напряжение  на шинах СН подстанции 2, а затем отвечающее ему действительное напряжение на этих шинах .

       Далее ведется расчет для линии ЛЧ, причем потери напряжения в ней определяется по найденному напряжению U_2c, т.е.

.

При этом напряжение в т.3  U₃= U_2c-D U₄

Еcли надо вычислить напряжение на шинах низкого напряжения (НН) подстанций, то расчет должен быть дополнен еще одним этапом. Должны быть учтены потери напряжения в сопротивлениях трансформаторов и автотрансформаторов и наличие магнитной связи между их обмотками.

Покажем последовательность  расчета на примере подстанции 1 предыдущей схемы.

На рисунке показана схема соединения элементов, учтенных при определении расчетной нагрузки этой подстанции 1 и указаны мощности, которые должны быть найдены и просуммированы при вычислении .

Так как напряжение U₁ известно (определено на предыдущем этапе расчета), то потеря напряжения в сопротивлении трансформатора Z_т1 может быть найдена по величине напряжения U₁ и мощности , протекающей по сопротивлению Z_т1 .

       При этом потеря напряжения

,

а приведенные напряжения на шинах низкого напряжения подстанций

.

Искомое напряжение на шинах НН подстанции 1

.

Можно применять и способ, предусматривающий приведение параметров схемы и ее режима к одной ступени трансформации. В нашем примере целесообразно привести сопротивление линии ЛЧ к номинальному напряжению 110 кВ. В этом случае из схемы замещения исключается идеальный трансформатор, точки объединяются, а сопротивления Z₄ заменяется сопротивлением:    

Напряжение в точке 3 при расчете также следует принимать приведенным к той же ступени трансформации, что и , т. е. считать, что . Оба подхода к расчету равноценны.

Расчеты режима линий с двусторонним питанием при различающихся напряжениях источников питания (по концам)

Для расчета схем с несколькими независимыми источниками питания широко используется принцип наложения.

Согласно этому принципу токи и мощности в ветвях могут рассматриваться как результат суммирования ряда слагающих, число которых равно числу независимых источников напряжения.

Каждый из этих токов определяется действием лишь одного из источников напряжения при равенстве нулю напряжений других источников.

Линии с двусторонним питанием при различающихся напряжениях по концам относятся к числу электрических цепей с независимыми источниками мощности. Для её расчета также может быть применен принцип наложения.

Заданы различные напряжения по концам линии, например U₁ >U₄.

Известны мощности нагрузок  S₂ и S₃ и сопротивления участков линии  Z_{kj ,} где k – узел начала участка линии, j – узел конца участка линии.

 Надо найти потоки мощности  S_kj.

В соответствии с известным из ТОЭ принципом наложения, линию можно представить двумя линиями (рисунок б) и в)).

Потоки мощности в исходной линии можно получить в результате наложения (суммирования)

потоков в этих линиях. Потоки мощности в линии с равными напряжениями по концам ( U_н.)

рисунок б) определяются известными выражениями:

                                              где       

                                              где        

В линии на рисунке в) в направлении от источника питания с большим напряжением к источнику с меньшим напряжением протекает сквозной уравнительный ток  I_ур. и уравнительная мощность S_ур.

 

                                                   

                                  

Соответственно в результате положения потоков, определенных по формулам (1), (2) и (3), определяются потоки мощности в линии с двусторонним питанием на рисунке а)

Определение потерь мощности  DS_{kj осуществляется по формуле:}

                               

    где   k – узел начала участка линии;

             j – узел конца участка линии;

Затем определяются напряжения.

Допустим точкой потокораздела является точка3,рисунок 2).Разрежем линию в узле 3, рис. д )

Теперь можно определить напряжения или падения напряжения ( DU_нб ) в двух разомкнутых сетях, т.е. в линиях 1–3 и 4–3¹ т.к. U₁ > U₄, то DU_1-3 > DU_4-3  и  DU_нб = DU_1-3

Послеаварийные режимы

Наиболее тяжелые – выход из строя и отключение участков 1-2 и 3-4 (ближайших к источнику питания ).

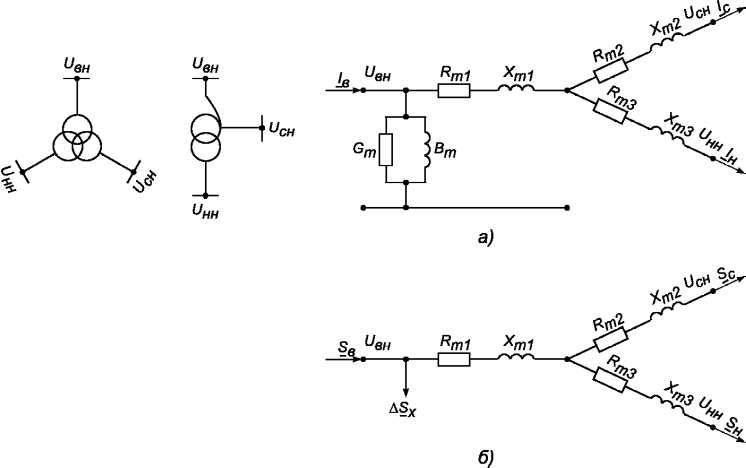Проанализируем эти режимы и определим наибольшую потерю напряжения  DU_нб в режиме, когда отключен участок 4-3 рисунок е). Обозначим наибольшую потерю напряжения  DU_{1-3 ав.}

В режиме, когда отключен участок 1-2 (рисунок ж)),наибольшую потерю напряжения обозначим  DU_{4-2 ав.}

Надо сравнить  DU_{1-3 ав.} и DU_{4-2 ав.}и определить наибольшую потерю напряжения  DU_ав.нб  Если линия с двусторонним питанием имеет ответвления —–  ( рисунок  з))

Рекомендуем посмотреть лекцию “10 Место и время пересечения таможенной границы”.

     ,то определение наибольшей потери напряжения усложняется.

Так, в нормальном режиме надо определить потери напряжения DU_1-3, DU_4-3, DU_1-2-5, сравнить их и определить DU_нб.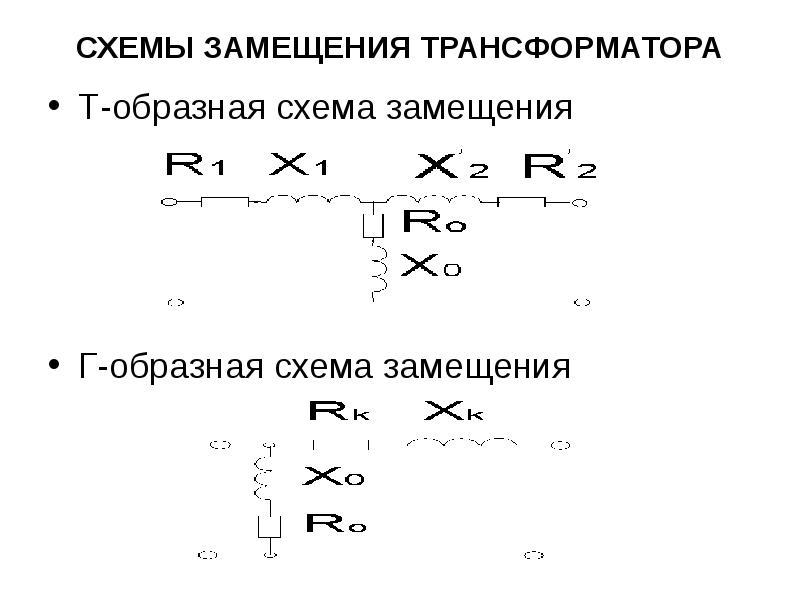

Далее чтобы определить  DU_нб.ав. в послеаварийном режиме, надо рассмотреть аварийные отключения головных участков 1-2 и 4-5.

Схемы замещения трансформатора – Энциклопедия по машиностроению XXL

Полная схема замещения индуктора, подобная схеме замещения трансформатора, приведена на рис. 5-4, а [24 ]. На схеме и х а — первичная и вторичная реактивности рассеяния, Хд = причем — магнитное сопротивление участка пути магнитного потока вне индуктора и загрузки, которое в дальнейшем называется магнитным сопротивлением обратного замыкания магнитного потока. Га и Хам—активное и внутреннее реактивное сопротивления загрузки, приведенные к току участка индуктора бесконечной длины. Сопротивления и Ха определяются в зависимости от формы тела и режима нагрева так, как было описано раньше. Реактивное сопротивление Хд определяет составляющую магнитодвижущей силы, необходимой для преодоления магнитным потоком пространства вне индуктора.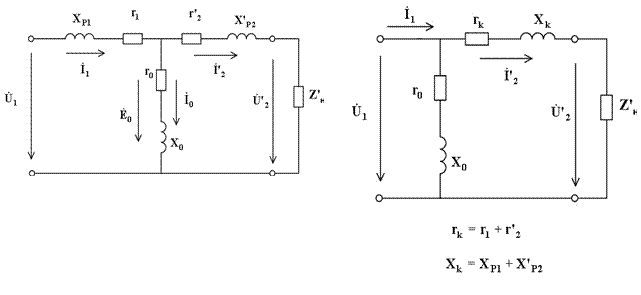  [c.77]
Применяя схемы замещения трансформатора с подвижными обмотками (рис. 27 Л 28) и задаваясь напряжением сварочной дуги я ее сопротивлением, определим необходимые параметры для построения векторной диаграммы. Индуктивное сопротивление вторичной обмотки трансформатора в приведенной форме имеет вид   [c.36]

Схемы замещения трансформатора 35  [c.205]

В рассматриваемом случае такая схема замещения в виде воздушного трансформатора обеспечивает правильность расчета напряженностей поля, токов и мощностей. Однако в более общем случае ее применение требует дополнительных условий или вообще невозможно. Если цилиндрическая система содержит массивное немагнитное тело, то ток в нем распределен неравномерно и замена его одним контуром неприемлема. Выходом является разбиение (дискретизация) такого тела по радиусу и длине на кольцевые элементы, являющиеся трубками тока, в пределах которых плотность тока примерно постоянна.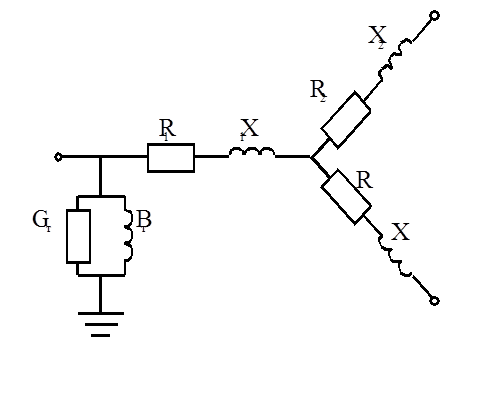 На этом приеме основан интегральный метод расчета цилиндрических и плоских систем с немагнитными телами (глава 2). Для массивных тел более сложной формы (например, призм) заранее выделить трубки вихревого тока уже нельзя  [c.15]

Измерение тока точечных и роликовых однофазных машин в пределах 3,5—35,0 ка может быть произведено прибором АСТ-2, работающим по схеме замещения, принцип которой заключается в следующем. В моменты пауз (при отсутствии тока) на гальванометр подается питание от стабильного источника постоянного тока—сухого элемента в момент измерения (нри протекании тока во- вторичном контуре) ток сухого элемента замещается равным по величине током с тороида (трансформатора с немагнитным сердечником).  [c.171]

Откуда полное сопротивление обмоток трансформатора в рассматриваемой схеме замещения  [c.36]

На рис. 27. изображена Т-образная схема замещения трансформатора, показанного на рис. 26. Участок аб этой схе.мы представляет собой намагничивающий контур, по которому протекает ток холостого хода /х. Активная составляющая /.,а обусловлена потерями в стали магнитопровода, а реактивная составляющая / р предназначена для создания основного магнитного потока трансформатора. Принимая во иним ине выражения, призе юииые для oдн JфaJ J о ансфирма1ора в режиме холостого хода, с >четом рассматриваемом схемы замещения  [c.35]

Рассмотрим процесс разрядки конденсатора С/ на импульсный трансформатор ИТр. Схема замещения представлена на рис. 1.6,5, где Li и Li — индуктивности первичной и вторичной обмоток Ri и Ri — активные сопротивления соответствующих проводов и обмо-гок Сг — паразитные емкости вторичной обмотки и проводов i — емкость формирующего конденсатора (паразитными емкостями на стороне первичной обмотки можно пренебречь ввиду их малости по сравнению с i. Между обмотками трансформатора действует взаимная индуктивность М. Сопротивление газоразрядного прибора Л  

[c.11]

Схема замещения представляет собой систему индуктивно связанных колебательных контуров. Решение уравнений, описывающих подобную систему, позволяет установить аналитические зависимости между токами и напряжениями на элементах схемы замещения в функции времени [8—10]. Пробой ГРП происходит под действием приложенного напряжения, возникающего на вторичной обмотке трансформатора, яоэтому основное внимание сосредоточим а характере изменения этого напряжения.  [c.12]

Применение схем замещения или двойного уравновешивания возможно лишь в сравнительно узком диапазоне частот, так как трудно иметь в одном приборе набор безреактивных сопротивлений, необходимых для измерения е и б образцов разнообразных изоляционных материалов в большом интервале частот 10 . . . 10 гц. Поэтому рассмотренные выше схемы с переменным 7 используют при фиксированной частоте, обычно 1000 гц. Если необходимо снимать частотные зависимости е и б, то для этой цели часто применяют неуравновешенный ди еренциальный мост (рис. 3-8, а, б). Два плеча моста образованы двумя вторичными полуобмотками дифференциального трансформатора, третье плечо представляет собой образцовый переменный конденсатор, четвертое — испытуемый образец. В измерительной диагонали включено высокоомное образцовое сопротивление напряжение в диагонали моста измеряется вольтметром Уц с высокоомным входом й с малой входной емкостью Сд. К достоинствам этого метода относятся возможность изменения частоты в широких пределах, наличие только одного регулируемого элемента — образцового конденсатора — и возможность отсчета б по шкале стрелочного прибора, измеряющего напряжение Уд в диагонали моста. то напряжение пропорционально разности токов, протекающих через конденсаторы С и С . При условии равенства емкостей  

[c.64]

В настоящее время чисто транзитные Л. э. встречаются реже, чем электропередачи с несколькими нагрузками вдоль линии или Л. о., образующие сети энергетич. систем. Такие более сложные случаи электрич. расчета целесообразнее производить, идя от участка к участку, т. е. находя в первой стадии расчета напряжения и токи высшей стороны повысительных и понизительных трансформаторов, и затем уже во второй стадии расчета учитывать трансформаторы соответствующим пересчетом напряжений, приняв во внимание потери напряжения в трансформаторах и установленные ответвления на обмотках их. При этом оказывается, что если вместо токов в электрич. расчете таких электропередач оперировать с мощностями, то помимо сокращения счетной работы уменьшается в приближенных способах и процент ошибки. Кроме того при методе мощностей влияние различных факторов на электрич. состояние линии становится более наглядным. Работа электропередачи с точки зрения условного раздельного рассмотрения активной и реактивной мощностей такова потребители, например асинхронные двигатели, требуют для своей нормальной работы наличия как активной, так и реактивной мощностей, из которых первая идет на механич. эффект двигателя, а вторая — на создание магнитных полей, без которых двигатель работать не будет. Задачей генераторной станции является т. о. выработка в необходимых размерах активной и реактивной мощностей, а задачей электропередачи, то есть линии и трансформаторов, — передача этих мощностей. Но передача электрич. энергии по проводам и через трансформаторы происходит с потерями активной и реактивной мощностей, благодаря чему активные и реактивные мощности, подаваемые генераторной станцией, будут больше потребляемых на величину активных и реактивных потерь мощности. Величина реактивной мощности в особенности сильно влияет на величину потери напряжения в электропередаче. Поэтому, желая иметь в зависимости от нагрузки те или иные напряжения по концам электропередачи, изменяют величину реактивных потерь мощности, уменьшая или увеличивая по электропередаче проходящую реактивную мощность, заставляя для этого работать синхронные или асинхронные к( 1пенсаторы на конце линии генераторами или потребителями реактивной мощности. В методе мощностей для отдельных участков Л. э. берется П-образная схема замещения, причем реактивные мощности участков, обусловленные емкостью самой линии и разнесенные по половине на начало и конец участка, включаются в реактивные мощности потребителей или ста1 ций, предварительно приведенные к высшему напряжению. Т. о. расчетной схемой отдельных участков является схема, состоящая только из последовательно включенных активного и реактивного сопротивлений линии. Реактивные составляющие  

[c.72]

На основании упрощенной схемы замещения составн.м уравнение для сварочного тока трансформатора с подвижными обмотками   [c.37]

При моделировании механической системы схема замещения упругого элемента, не имеющего массы, представляет собой четырехполюсник, содержащий один конденсатор С по первой системе аналогий или один элемент самоиндукции Ь по второй системе аналогий. Сосредоточенная масса, наоборот, замещается индуктивностью по первой системе аналогий и емкостью по второй. Модели элемента трения — это четырехполюсники, содержащие омические сопротивления Я или проводимости Рычаг или редуктор представлен четырехполюсником в виде трансформатора. Коэффициент трансформации соответсгвует передаточному числу редуктора или рычага.  [c.290]

---

128. Назначение, принцип работы, схема замещения и погрешность измерительных трансформаторов тока и напряжения.

ТА

Принцип действия. Трансформаторы тока (ТТ) являются вспомогательными элементами, с помощью которых ИО РЗ получают информацию о значении, фазе и частоте тока защищаемого объекта. От достоверности получаемой информации зависит правильность действия устройств РЗ. Поэтому основным требованием к ТТ, питающим устройства РЗ, является точность трансформации контролируемого тока с погрешностями, не превышающими допустимых значений. Принцип устройства ТТ поясняют схемы, приведенные на рис.3.1. Заметим, что один из вторичных зажимов ТТ должен обязательно заземляться по условиям техники безопасности.

Трансформатор тока (рис.3.1, а) состоит из первичной обмотки w₁, включаемой последовательно в цепь контролируемого тока, вторичной обмотки w₂, замкнутой на сопротивление нагрузки Z_н, состоящее из последовательно включенных элементов РЗ или измерительных приборов, и стального магнитопровода 1, с помощью которого осуществляется магнитная связь между обмотками. Первичный ток I₁ проходящий по виткам первичной обмотки w_l, и ток I₂, индуцированный во вторичной обмотке

w₂, создают магнитодвижущие силы (МДС) I₁w_l и I₂w₂, которые вызывают соответственно магнитные потоки Ф₁ и Ф₂, замыкающиеся по стальному магнитопроводу 1. Намагничивающие силы и создаваемые ими магнитные потоки с учетом их положительных направлений, показанных на рис.3.1, геометрически вычитаются, образуя результирующую МДС I_намw₁ и результирующий магнитный поток трансформатора Ф_т [41]:

                                  (3.1)

                                              (3.1а)

Поток Ф_т, называемый рабочим или основным, пронизывает обе обмотки и наводит во вторичной обмотке ЭДС Е₂, которая создает в замкнутой цепи вторичной обмотки ток I₂. Поток Ф_т создается МДС I_намw₁ и, следовательно, током I_нам. Последний является частью тока I₁ и называется намагничивающим током. Если I_нам = 0, выражение (3.1) примет вид

I_lw_l = I₂w₂,

откуда

                                                                                                    (3.2)

где  – коэффициент трансформации, называемый витковым, в отличие от номинального¹. При отсутствии намагничивающего тока вторичный ток I₂ (расчетный ток) равен первичному току I₁ поделенному на коэффициент трансформации ТТ, равный К_Iв. В этом случае первичный ток полностью трансформируется во вторичную обмотку w₂, и ТТ работает идеально без потерь и погрешностей.

Причины погрешности. В реальном ТТ I_нам ≠ 0, как это следует из (3.1). Ток I_HAM является обязательной частью первичного тока I₁, он образует МДС, создающую поток Ф, который и осуществляет трансформацию. Из выражения (3.1) вторичный ток реального ТТ

                                                                           (3.3)

где k_I = w₂/w_l – витковый коэффициент трансформации.

Из выражения (3.3) следует, что действительный вторичный ток I₂ отличается от расчетного (идеального) значения I₁/k_I, определенного по формуле (3.2), на значение I_нам/k_I, которое вносит искажение в абсолютное значение и фазу вторичного тока. Таким образом, причиной, вызывающей погрешность в работе ТТ, является ток намагничивания I_нам

Векторная диаграмма и виды погрешностей ТТ. Искажающее влияние тока намагничивания на вторичный ток ТТ показано на векторной диаграмме рис.3.3, в основу которой положена схема замещения (см. рис.3.1, б).

В схеме замещения магнитная связь между первичной и вторичной обмотками ТТ заменена электрической, а все величины первичной стороны приведены к виткам вторичной обмотки: I’₁= I₁/K_I и I’_нам= I_нам/k_I.

Погрешность по току ΔI (f_i,) и полная погрешность ε =|I_нам| выражаются в относительных единицах или процентах как отношение действующих значений этих погрешностей к действующему значению приведенного первичного тока.

Относительная токовая погрешность

                                                                                    (3.5)

Относительная полная погрешность

                                                                                           (3.6)

  
 

* Ток I’_нам имеет две составляющих: I’_a нам, которая определяет потери энергии на нагрев магнитопровода вихревыми токами, и I’_р нам, которая осуществляет намагничивание сердечника, т. е. создает поток Ф_т. Составляющая I’_a нам << I’_р нам, поэтому углом γ можно пренебречь и считать, что вектор I’_нам совпадает по фазе с Ф_т и равен I’_р нам.

Если вторичный ток несинусоидален, то ток намагничивания выражается как среднее квадратичное значение разности мгновенных значений реального и расчетного токов i₂:

Тогда

                                                                                (3.7)

Здесь К_I – номинальный коэффициент трансформации ТТ.

Погрешность по углу выражается в градусах и минутах, она считается положительной, если I₂ опережает I^’₁, как показано на рис.3.3. Относительные погрешности ε, , f_i и δ увеличиваются с увеличением тока намагничивания I_нам.

           

TV

 

Информацию о контролируемом напряжении ИО РЗ получают от первичных трансформаторов напряжения (ТН). Основными параметрами ТН (рис.6.1) являются: номинальное первичное напряжение U_1ном (равное номинальному напряжению контролируемой электрической сети), вторичное номинальное напряжение U_2ном, значение которого обычно принимается равным 100 или 100/В. Отношение этих величин, называемое номинальным коэффициентом трансформации, К_Uном = U_1ном/ U_2ном [24].

Начала и концы первичных и вторичных обмоток ТН Н (н) и К (k) обозначаются изготовителями так же, как и у силовых трансформаторов: у первичной обмотки буквами А и X, у вторичной соответственно а и х. Для питания устройств РЗ используются в большинстве случаев ТН, установленные на сборных шинах ПС и РУ электростанций, к вторичным обмоткам которых подключаются РЗ всех присоединений (рис.6.2, а), или на каждом присоединении, питающие РЗ только этого присоединения.

 ПОГРЕШНОСТИ ТРАНСФОРМАТОРА НАПРЯЖЕНИЯ

 

Трансформатор напряжения работает с погрешностью, искажающей вторичное напряжение как по величине, так и по фазе. В “идеальном” ТН, работающем без погрешностей, вторичное напряжение

                                                                                                          (6.1)

где U₁ – напряжение, подведенное к зажимам первичной обмотки; К_U – коэффициент трансформации “идеального” ТН, равный отношению количества витков первичной и вторичной обмоток. Однако за счет падения напряжения ΔU (рис.6.4, б) в первичной и вторичной обмотках действительное значение вторичного напряжения будет равно:

                                                                                                      (6.2)

что вытекает из эквивалентной схемы замещения ТН и векторной диаграммы (рис.6.4, а, б). Из этой же схемы следует

                                                                                      (6.2а)

Падение напряжения в обмотках ТН ΔU обусловливает появление погрешности, искажающей значение и фазу U₂ (рис.6.4, б) по сравнению с расчетным напряжением U₂ = U₁/K_U = U’₁ по выражению (6.1).

Поскольку значения Z₁ и Z₂, а также ток намагничивания I_нам определены конструкцией ТН, в условиях эксплуатации уменьшить его погрешность можно только уменьшением тока

нагрузки I₂. Допустимые погрешности нормируются при номинальном напряжении, соответственно чему ТН подразделяются на классы: 0,2; 0,5; 1 и 3. Один и тот же ТН может работать в разных классах точности в зависимости от значения нагрузки. Заводы обычно указывают номинальную мощность, подразумевая под ней максимальную нагрузку, которую может питать ТН в гарантированном классе точности. Кроме того, для ТН указывается максимальная мощность по условиям нагрева, которая значительно превосходит его номинальную мощность. Погрешность по значению вторичного напряжения принято оценивать в процентах:

                                                                                            (6.3)

Погрешность по фазе оценивается углом сдвига δ между векторами первичного и вторичного напряжений (рис.6.4, б).

В начало

“Определение параметров схемы замещения трансформаторов”

Практическая работа №7

Определение параметров схемы замещения трансформатора

Задание: Трехфазный трансформатор имеет параметры, значения которых приведены в таблице 1: номинальная мощность S_ном и номинальные напряжения (линейные) U_1ном и U_2ном, напряжение короткого замыкания u_к, ток холостого хода i₀ , потери холостого хода P_0ном и потери короткого замыкания P_к.ном . Обмотки трансформатора соединены по схеме «звезда-звезда».

Требуется определить: параметры Т-образной схемы замещения, считая ее симметричной ( r₁ = r₂^′ и x₁ = x₂^′), а также фактические значения сопротивлений вторичной обмотки; величины КПД η, соответствующие значениям полной мощности трансформатора 0,25 S_ном; 0,5 S_ном; 0,75 S_ном и S_ном при коэффициентах мощности нагрузки cosφ₂=0,8 (индуктивный характер нагрузки) и cosφ₂=1; номинальное изменение напряжения ∆U_ном. Построить графики η= f(β) и U₂ = f(β).

Таблица 1

Методические указания

1. Напряжение короткого замыкания

U_1к = 10^-2 u_к U_1ном

2. Ток короткого замыкания

I_1к = I_1ном = S_ном/( U_1ном)

3. Коэффициент мощности в режиме короткого замыкания

сosφ_к = P_к/( U_1к I_1к )

4. Полное сопротивление короткого замыкания

z_к = U_1к/( I_1к)

5. Активная составляющая сопротивления короткого замыкания

r_к = z_к cosφ_к

6. Индуктивная составляющая сопротивления короткого замыкания

x_к = z_к sinφ_к

7. Активные и индуктивные сопротивления Т-образной схемы замещения трансформатора

r₁ = r₂^′= 0,05/2

x₁ = x₂^′= 0,13/2

8. Фактические (неприведенные) значения сопротивлений вторичной обмотки трансформатора

r₂= r₂^′/( U₁/ U₂)²

x₂ = x₂^′/( U₁/ U₂)²

9. Ток холостого хода

I_0ном = 10^{-2 .} 6,5 ^. i₀ I_1ном

10. Коэффициент мощности в режиме холостого хода

сosφ₀ = P_0ном /( I_0ном U_1ном)

11. Полное сопротивление ветви намагничивания Т-образной схемы замещения трансформатора

z_m = U_1ном/( I_0ном)

12. Активное и индуктивное составляющие ветви намагничивания

r_m= z_m сosφ₀

x_m = z_m sinφ₀

13. Для расчета КПД воспользуемся выражением

η =

Задавшись значениями коэффициента нагрузки: β = 0,25; 0,50; 0,75 и 1,0 рассчитаем для каждого из них КПД сначала для коэффициента мощности нагрузки сosφ₂ = 1, а затем для сosφ₂ = 0,8

Результаты расчетов занесем в таблицу

Построить график зависимости η= f(β)

Эквивалентная схема трансформатора | electricaleasy.com

В практическом трансформере –
(a) Некоторый поток утечки присутствует как на первичной, так и на вторичной стороне. Эта утечка приводит к возникновению реактивных сопротивлений утечки с обеих сторон, которые обозначаются как X ₁ и X ₂ соответственно.
(b) И первичная, и вторичная обмотки обладают сопротивлением, обозначенным как R ₁ и R ₂ соответственно. Эти сопротивления вызывают падение напряжения, как I ₁ R ₁ и I ₂ R ₂ , а также потери в меди I ₁ ² R ₁ и I ₂ ² R ₂ .
(c) Проницаемость сердечника не может быть бесконечной, поэтому необходим некоторый ток намагничивания. Взаимный поток также вызывает потери в сердечнике в железных частях трансформатора.
Нам необходимо учесть все вышеперечисленное, чтобы вывести эквивалентную схему трансформатора .

Эквивалентная схема трансформатора Сопротивления и реактивные сопротивления трансформатора, которые описаны выше, можно представить отдельно от обмоток (как показано на рисунке ниже). Следовательно, функция обмоток в дальнейшем будет только преобразовывать напряжение.
Ток холостого хода I ₀ делится на чистую индуктивность X ₀ (с учетом намагничивающих компонентов I _μ ) и неиндукционное сопротивление R ₀ (с учетом рабочего компонента I _w ), которые соединены параллельно. Главная. Значение E ₁ может быть получено путем вычитания I ₁ Z ₁ из V ₁ . Значение R ₀ и X ₀ можно рассчитать как, R ₀ = E ₁ / I _w и X ₀ = E ₁ / I _μ .

Но использование этой эквивалентной схемы не упрощает вычислений. Чтобы упростить вычисления, предпочтительно передавать ток, напряжение и полное сопротивление либо на первичную, либо на вторичную стороны. В этом случае придется работать только с одной обмоткой, что удобнее.

Из коэффициента трансформации напряжения видно, что
E ₁ / E ₂ = N ₁ / N ₂ = K

Теперь давайте отнесем параметры вторичной стороны к первичной.
Z ₂ может называться первичным как Z ₂ ‘
, где Z ₂ ‘ = (N ₁ / N ₂ ) ² Z ₂ = K ² Z ₂ . ………… где K = N ₁ / N ₂ .
, то есть _R ‘+ jX ₂ ‘ = K ² ( ₂ + jX ₂ )
приравнивая действительную и мнимую части,
R ₂ ‘= K ² R ₂ и X ₂ ‘= K ² X ₂ .
И В ₂ ‘= КВ ₂
На следующем рисунке показана эквивалентная схема трансформатора с параметрами вторичной обмотки относительно первичной обмотки .

Теперь, когда значения сопротивления обмотки и реактивного сопротивления утечки настолько малы, что V ₁ и E ₁ можно считать равными. Следовательно, возбуждающий ток, потребляемый параллельной комбинацией R ₀ и X ₀ , не повлияет существенно, если мы переместим его на входные клеммы, как показано на рисунке ниже.

Теперь пусть R ₁ + R ₂ ‘= R’eq и X ₁ + X ₂ ‘ = X’eq
Тогда эквивалентная схема трансформатора станет такой, как показано на рисунке ниже
.

Примерная схема замещения трансформатора

Если рассчитывается только регулировка напряжения, то можно пренебречь даже всей ветвью возбуждения (параллельная комбинация R0 и X0). Тогда эквивалентная схема станет такой, как показано на рисунке ниже
.

Что такое эквивалентная схема трансформатора?

Equivalent Circuit of Transformer – это электрическая схема, объясняющая уравнения, представляющие поведение этого трансформатора.Фактически, эквивалентная схема любого электрического прибора важна для анализа его работы и выявления любых возможностей дальнейшего изменения моделирования. Эквивалентная схема трансформатора включает в себя настройку индуктивности, сопротивления, напряжения, емкости и т. Д. Эти схемы затем можно анализировать и исследовать, применяя принципы теории диаграммы.

Что такое эквивалентная схема трансформатора?

Эквивалентная схема или диаграмма любой системы может быть относительно полезной для предварительного определения характеристик прибора в различных ситуациях различных операций.Он может легко представить поведение схемы с помощью конкретного уравнения, полностью описывающего состояние системы.

Например, эквивалентный импеданс системы жизненно важен для оценки, поскольку трансформатор является электрическим силовым прибором для рассмотрения нескольких характеристик электрического силового устройства, которые могут потребоваться для оценки всего внутреннего импеданса трансформатора в системе электроснабжения. , исследование с первичной или вторичной стороны в зависимости от требований.

Эта оценка фактически требует эквивалентной схемы трансформатора на основе основной стороны эквивалентной схемы трансформатора и вторичной стороны соответственно. Относительный импеданс также является очень важной характеристикой трансформатора. Посетите здесь, чтобы увидеть важность этого расчета при проектировании любой схемы.

Упрощенная эквивалентная схема трансформатора представлена ​​с учетом всех свойств трансформатора на первичной или вторичной стороне.Основная эквивалентная схема трансформатора показана ниже на схеме:

Эквивалентная схема трансформатора (Ссылка: circuitglobe.com )

Этой особенности следует уделять большое внимание при установке трансформатора в существующий система электроснабжения. Относительный импеданс различных силовых трансформаторов должен быть полностью согласован на основе параллельной конфигурации энергосистем. Относительный импеданс можно извлечь из эквивалентного значения импеданса трансформатора, поэтому можно заметить, что эквивалентная схема трансформатора также важна при оценке относительного импеданса.

Мы можем определить эквивалентную схему трансформатора на основе коэффициента трансформации как:

K = \ frac {{E} _ {2}} {{E} _ {1}}

Где E ₁ – наведенная ЭДС, равная основному используемому напряжению ( ₁ В) с небольшим уменьшением напряжения. Это напряжение влияет на систему, вырабатывая ток I ₀ или ток холостого хода в первой обмотке трансформатора. Величина тока холостого хода слишком мала, поэтому при расчетах им можно пренебречь.

В первую очередь мы должны установить общие правила в системе для управления эквивалентной схемой трансформатора, затем мы можем изменить ее для подготовки к определению правил на основе первичной обмотки. Для этого, во-первых, нам необходимо представить полную векторную диаграмму трансформатора, которая представлена ​​на рисунке ниже.

Векторная диаграмма трансформатора (Ссылка: lectric4u.com )

В результате I ₁ = I ’ ₁ . Далее ток холостого хода разделен на две части: намагниченный ток (I _m ) и рабочий ток (I _w ).{‘}} {K} = \ frac {{I} _ {1} – {I} _ {0}} {K}

Напряжение подключения V ₂ внутри нагрузки такое же, как и конкретная ЭДС E ₂ в следующей обмотке с небольшим понижением напряжения во второй обмотке.

Эквивалентная схема трансформатора, когда все величины относятся к первичной стороне

В этом методе, чтобы получить эквивалентную схему трансформатора, все характеристики должны рассматриваться как первичная часть, как показано на рисунке ниже:

Эквивалентная цепь трансформатора, относящаяся к первичной стороне (Каталожный номер: circuitglobe.{‘}

Примерная эквивалентная схема трансформатора

Из-за небольшого значения I ₀ по сравнению с I ₁ , оно составляет менее 4 процентов от общей нагрузки первичного тока и изменяет снижение напряжения незначительно. В результате это идеальное приближение для уменьшения эффекта возбуждения схемы в приближенной эквивалентной схеме трансформаторного метода. Сопротивление и реактивное сопротивление обмотки расположены в последовательной конфигурации, которая теперь может быть введена как эквивалентное реактивное сопротивление и сопротивление трансформатора для любой конкретной стороны.{‘} = K {V} _ {2}

Приблизительная эквивалентная цепь трансформатора, относящаяся к первичной стороне (Ссылка: lectric4u.com )

Эквивалентная цепь трансформатора, когда все величины относятся к вторичной стороне

Эквивалентная схема трансформатора или базовая схема представлена ​​ниже, когда все функции спроектированы на основе вторичной обмотки. Эквивалентная цепь

, относящаяся к вторичной стороне (Ссылка: circuitglobe.com )

Следующие свойства представляют собой значения сопротивления и реактивного сопротивления, которые можно получить ниже.{‘}

Поскольку ток холостого хода или I ₀ обычно составляет от 2 до 4 процентов от значения полной нагрузки номинального тока, параллельная конфигурация включает сопротивление R ₀ , а реактивное сопротивление X ₀ может быть удаляется из схемы без внесения каких-либо особых ошибок в работу трансформатора при приложении нагрузки.

Мы также можем применить дальнейшее упрощение в эквивалентной схеме трансформатора, удалив параллельные члены в схеме, включая R ₀ и X ₀ .Эта упрощенная схема системы представлена ​​ниже:

Упрощенная эквивалентная схема трансформатора (Ссылка: circuitglobe.com )

Это все существенные проблемы, связанные с эквивалентной схемой трансформатора.

Эквивалентная схема трансформатора

– электротехническое руководство

Эквивалентная схема трансформатора показана на рисунке.

Компоненты без нагрузки

Первичный ток холостого хода I _o имеет две составляющие, а именно I _m и I _w .

Где I _м = намагничивающая составляющая = I _o sin φ _o
и I _w = компонент потерь в сердечнике = o cos φ _o .

• I _w обеспечивает потери холостого хода и, как предполагается, протекает через сопротивление холостого хода, которое также известно как сопротивление потерь в сердечнике (R _или ).
• Предполагается, что намагничивающая составляющая I _м протекает через реактивное сопротивление, известное как намагничивающее реактивное сопротивление, X _o .
• Параллельная комбинация R _o и X _o также известна как схема возбуждения .

Из эквивалентной схемы трансформатора ,

R _o = V ₁ / I _w и X _o = V ₁ / I 9182 _м.

Основные компоненты

• Сопротивление R ₁ и реактивное сопротивление X ₁ соответствуют сопротивлению обмотки (сопротивление постоянному току) и реактивному сопротивлению утечки первичной обмотки.
• Полный ток I ₁ на первичной стороне равен векторной сумме I _o и I ₂ ’.
• I ₂ ’= K I ² – дополнительный первичный ток, протекающий из-за нагрузки, подключенной на вторичной стороне трансформатора.

Вторичные компоненты

• Сопротивление R ₂ и реактивное сопротивление X ₂ соответствуют сопротивлению обмотки и реактивному сопротивлению утечки вторичной обмотки.
• Сопротивление нагрузки Z _L может быть резистивным, индуктивным или емкостным.
• Эквивалентная схема однофазного трансформатора дополнительно упрощена за счет переноса всех величин либо на первичную, либо на вторичную сторону.
• Это сделано для упрощения расчетов.

Все компоненты вторичной обмотки трансформатора переведены на первичную обмотку, как показано на рисунке.

• R ₂ ’, X ₂ ’ и Z _L ’являются значениями R ₂ , X ₂ и Z _L , относящимися к первичным соответственно.
• Значения этих компонентов получаются следующим образом:

R ₂ ‘= R ₂ / K ² , X ₂ ‘ = X ₂ / K ² и Z _L ‘= Z _L / K ²

где K = N ₂ / N ₁ (коэффициент трансформации).

Эквивалентная цепь трансформатора, относящаяся к вторичной обмотке

Эквивалентная схема трансформатора , относящаяся к вторичной стороне, показана на рисунке.

• Компоненты R ₁ ’, X ₁ ’, R _o ’и X _o ’ являются первичными компонентами, относящимися к вторичным. Выражения для этих компонентов следующие:

R ₁ ‘= K ² R ₁ , X ₁ ‘ = K ² X ₁
R _o ‘= K ² R _o , X _o ‘= K ² X _o

• Первичные напряжения и токи также передаются на вторичную сторону как I ₁ ‘, V ₁ ‘, I _o ‘, E ₁ ‘ соответственно и выдаются по:

I ₁ ‘= I ₁ / K, E ₁ ‘ = KE ₁ , I _o ‘= I / K
, где K = N ₂ / N ₁ (коэффициент трансформации).

Примерная эквивалентная схема трансформатора

Примерная эквивалентная схема – это схема, которая получается путем смещения схемы возбуждения влево от R ₁ и X ₁ , как показано на рисунке.

Хотя это смещение создает ошибку в падении напряжения на R ₁ и X ₁ , оно значительно упрощает работу по расчету и дает значительно упрощенную эквивалентную схему.

Трансформатор | Все сообщения

© https: // yourelectricalguide.ком / схема замещения трансформатора.

Схема трансформатора, эквивалентная

, относящаяся к первичной и вторичной обмоткам

По сути, эквивалентная схема представляет все параметры трансформатора в виде схемы или в виде диаграммы. Эквивалентную схему трансформатора можно использовать для понимания поведения трансформатора в различных условиях. Расчет различных параметров трансформатора, таких как сопротивление, реактивное сопротивление, импеданс на первичной и вторичной стороне, можно легко выполнить, что также используется для определения регулирования, эффективности и потерь трансформатора.

Схема эквивалента трансформатора:

Рассмотрим трансформатор с V ₁ и I ₂ – это первичное напряжение и ток. Аналогично, V ₁ и I ₂ – это вторичное напряжение и ток. Пусть E ₁ и E ₂ – это ЭДС, индуцированные в первичной и вторичной обмотках соответственно, как показано ниже.

Для вышеуказанного трансформатора эквивалентная схема с коэффициентом трансформации K показана ниже.

На приведенной выше принципиальной схеме первичный ток трансформатора обслуживает два компонента I _o и I ₂ . Ток холостого хода I _o , также известный как ток намагничивания, также создает магнитный поток и намагничивает сердечник с потерями в сердечнике.

• Потери в сердечнике (потери на гистерезис и потери на вихревые токи) представлены неиндуктивным сопротивлением R _o , принимая рабочий компонент I _w . Ток I _w , составляющий ток I _o протекает через сопротивление R _o , так что,
• ЭДС E ₁ , индуцированная в первичной обмотке из-за потока, создаваемого током намагничивания I _μ .Величина ЭДС E ₁ будет меньше и противоположна приложенному напряжению V ₁ . Реактивное сопротивление X _o из-за потока Φ, который подключен параллельно сопротивлению R _o , таково, что,

Здесь R ₁ X ₁ и R ₂ X ₂ – это падения, обусловленные сопротивлением первичной и вторичной обмоток и реактивным сопротивлением утечки соответственно. Ток I ₂ – это ток противовеса I ₂ вторичной обмотки на первичной обмотке.Теперь мы можем еще больше упростить эквивалентную схему, сдвинув первичные параметры на вторичную сторону, или наоборот, это снижает сложность схемы и вычислений. Это можно сделать, используя коэффициент трансформации трансформатора.

Эквивалентная цепь трансформатора относительно первичной обмотки:

Вышеупомянутая эквивалентная схема трансформатора может быть изменена путем передачи напряжения, тока и полного сопротивления вторичной стороны первичной стороне, как показано на рисунке ниже.

Путем передачи всех параметров вторичной стороны на первичную с коэффициентом трансформации K. Тогда

• Первичный эквивалент вторичной ЭДС,
• Первичный эквивалент вторичного напряжения на клеммах,
• Первичный эквивалент вторичного тока,
• Точно так же вторичное сопротивление, реактивное сопротивление и импеданс, называемые первичными, задаются как

Эквивалентная схема может быть дополнительно изменена путем переноса R _o и X _o (схема возбуждения) в сторону левого конца, известного как приблизительная эквивалентная схема, как показано на рисунке ниже.Ошибка, возникающая при этом, мала, и ею можно пренебречь. Следует отметить, что в этом случае R _o = V ₁ / I _w и X _o = V _o / I _μ .

Поскольку ток холостого хода I _o очень мал, схему можно дополнительно упростить, если пренебречь I _o , взяв I ₁ ‘= I ₁ , показанный на рисунке ниже. Здесь R ₀₁ (R ₁ + R ₂ ‘) и X ₀₁ (X ₁ + X ₂ ‘) – это полное эквивалентное сопротивление и реактивное сопротивление трансформатора, называемого первичным.

Эквивалентная цепь трансформатора относительно вторичной обмотки:

Точно так же, поскольку эквивалентная схема трансформатора относится к первичной обмотке, мы также можем отнести параметры первичной обмотки к вторичной стороне, перенеся первичную сторону на вторичную сторону, как показано ниже.

Путем передачи всех параметров первичной стороны на вторичную с коэффициентом трансформации K. Тогда

• Вторичный эквивалент первичной ЭДС,
• Вторичный эквивалент первичного напряжения,
• Вторичный эквивалент первичного тока,
• Аналогичным образом, сопротивление первичной обмотки, реактивное сопротивление и импеданс, называемые вторичной обмоткой, задаются как

Аналогичным образом, без учета тока холостого хода I _– упрощенная эквивалентная схема, относящаяся к вторичной обмотке, показана ниже.Здесь R ₀₂ (R ₁ ‘+ R ₂ ) и X ₀₂ (X ₁ ‘ + X ₂ ) – это полное эквивалентное сопротивление и реактивное сопротивление трансформатора, называемого вторичным.

Из вышеизложенного можно сделать вывод, что,

• Если параметры эквивалентной схемы упоминаются как первичные. Вторичные параметры должны быть разделены с коэффициентом трансформации K, за исключением вторичного тока, где он умножается.
• Если параметры схемы замещения относятся к вторичной.Первичные параметры должны быть умножены на коэффициент трансформации K, за исключением первичного тока, на который он делится.

Эквивалентная схема практического трансформатора – нестандартные катушки

Практический трансформатор и эквивалентные схемы

Обмотки трансформатора в основном изготавливаются из меди. Хотя медь является очень хорошим проводником, у нее все же есть внутреннее сопротивление. Следовательно, и первичная, и вторичная обмотки трансформатора имеют конечное сопротивление, а именно.R1 и R2. Эти сопротивления равномерно распределяются по обмоткам и вызывают потери в меди (I2R).

Будем считать, что ЭДС I1N1 в первичной обмотке индуцирует поток Φl1, ЭДС I2N2 во вторичных обмотках и поток утечки Φl2. Оба сопротивления считаются реактивным сопротивлением утечки обмоток трансформатора. Это последовательные эффекты на очень низких (50/60 Гц) рабочих частотах. Для простоты вычислений их можно рассматривать как сосредоточенные параметры.

Поэтому считается, что трансформатор состоит из сосредоточенных сопротивлений R1 и R2 и реактивных сопротивлений X l1 и X l2, включенных последовательно с соответствующими обмотками. Однако наведенные ЭДС E1 и E2 могут незначительно отличаться от вторичных напряжений V1 и V2 из-за наличия сосредоточенных импедансов. Это явление наблюдается из-за небольших падений напряжения на сопротивлениях обмоток R1 и R2 и реактивном сопротивлении утечки.

Приведенное ниже уравнение дает коэффициент трансформации как:
а = (N1 / N2) = (E1 / E2) ≈ (V1 / V2)

Практичный или неидеальный трансформатор

Эквивалентная схема

Теперь ток возбуждения I0‾ можно разделить на две составляющие Im‾ и Ii‾.Im‾ – его намагничивающая составляющая, которая создает взаимный поток Φ‾, а Ii‾ – составляющая потерь в сердечнике, которая обеспечивает потери, связанные с изменением магнитного потока. Его можно представить как
I0‾ = Im‾ + Ii‾

Здесь векторная форма обозначена отрицательным знаком (‾).

Следовательно, эквивалентная схема практического трансформатора может быть представлена, как показано на рисунке ниже

Эквивалентная схема трансформатора

Здесь
Gc = проводимость
Bm = Susceptance

Импеданс теперь можно отнести к первичной обмотке, в результате получится следующая цепь:

Эквивалентная схема, относящаяся к первичной стороне, выглядит следующим образом: (сердечник не учитывается)

Схема, эквивалентная первичной

X l2 ’= (N1 / N2) 2 X l2
R2 ’= (N1 / N2) 2 R2

Напряжение нагрузки и токи, относящиеся к первичной стороне, равны:

V2’ = (N1 / N2) V2
I2 ’= (N1 / N2) I2

V1’ = (N1 / N2) V1
I1 ’= (N1 / N2) I1
Gi ’= (N1 / N2) 2 Gi
Bi ’= (N1 / N2) 2 Bi
X l1 ’= (N1 / N2) 2 X l1
R1 ’= (N1 / N2) 2 R1

Фазорная диаграмма

Применение закона Кирхгофа о напряжении на первичной и вторичной обмотках эквивалентных схем

V1¬ = E1 + I1R1 + jI1X1
V2¬ = E2 + I2R2 + jI2X1
I1 = I2 ’+ I0’ = I2 ’+ (Ii + Im)

Используя эти уравнения, векторную диаграмму практического трансформатора можно составить следующим образом:

Фазорная схема эквивалентной цепи практического трансформатора

Теория эквивалентной схемы трансформатора

Что такое эквивалентная схема трансформатора?

Прежде чем обсуждать эквивалентную схему трансформатора, необходимо разобраться в практическом применении трансформатора.Практический трансформатор всегда имеет сопротивления обмоток, которые играют основную и важную роль в потерях в меди . Так как сопротивление первичной обмотки составляет R ₁ , а вторичной обмотки – R ₂ . По сути, часть потока первичной обмотки, а также вторичная обмотка завершают путь через воздух и соединяются с соответствующей обмоткой. Такой поток называется потоком утечки.

Поток утечки через первичную обмотку создается за счет первичного тока I ₁ , который находится в фазе с I ₁ и связан только с первичной обмоткой, в то время как поток утечки через вторичную обмотку создается за счет тока I ₂ , который находится в фазе с I ₂ и также связан с вторичной обмоткой.Из-за этих потоков утечки там присутствуют соответствующие самоиндуцированные ЭДС, и из-за этих самоиндуцированных ЭДС первичное напряжение V ₁ должно преодолеть первичную самоиндуцированную ЭДС, чтобы создать E ₁ на первичной обмотке. в то время как E ₂ , индуцированный на вторичной обмотке, должен преодолеть вторичную самоиндуцированную ЭДС, чтобы произвести V ₂ под нагрузкой, из-за чего эти самоиндуцированные ЭДС рассматриваются как фиктивные падения напряжения на реактивных сопротивлениях X ₁ и X ₂ , играющие свою основную роль вместе с последовательными сопротивлениями первичной и вторичной обмоток R ₁ и R ₂ соответственно.

Мы знаем, что если сопротивление и реактивное сопротивление системы заданы, мы можем найти импеданс, поскольку мы знаем, что импеданс – это комбинированный эффект реактивных сопротивлений и сопротивлений системы. Как мы знаем, первичные и вторичные сопротивления и реактивные сопротивления равны R ₁ , R _2, и X ₁ , X ₂ соответственно.

Расчеты – Эквивалентная схема трансформатора

Следовательно, импеданс первичной и вторичной обмоток составляет

Z ₁ = R ₁ + jX ₁

Z ₂ = R ₂ + jX ₂

И соответствующие им величины равны,

Z ₁ = (R ₁ ² + X ₁ ² ) ^1/2

Z ₂ = (R ₂ ² + X ₂ ² ) ^1/2

Комбинация фиксированных и переменных сопротивлений и реактивных сопротивлений, которые точно имитируют характеристики и работу машина известна как эквивалентная схема машины.

Для трансформатора первичный ток холостого хода состоит из двух компонентов:

Компонент намагничивания = I _м = I _o sinϕ _o

Активный компонент = I _c = I _o cosϕ _o

Намагничивающая составляющая тока холостого хода создает магнитный поток и, как предполагается, протекает через реактивное сопротивление X _o , в то время как активная составляющая тока холостого хода, представляющая потери в сердечнике, как предполагается, протекает через сопротивление R _o .Таким образом, эта схема, содержащая параллельно R _o и X _o , называется схемой возбуждения. Итак, мы можем написать

R _o = V ₁ / I _c

X _o = V _{1 1 m}

Мы знаем, что когда нагрузка подключенный ко вторичной обмотке трансформатора, ток I ₂

протекает через нагрузку, из-за чего происходит падение напряжения на R ₂ и X ₂ , и из-за этого тока I ₂ первичная обмотка потребляет дополнительную ток, который равен

I ₂ ^‘ = KI ₂ , где K – постоянная преобразования напряжения.

Теперь мы можем сказать, что I ₁ является векторным сложением I _o и I ₂ ^’, и этот ток первичной обмотки вызывает падение напряжения на R ₁ и X ₁ .

Его можно записать как

I ₁ = I _o + I ₂ ^‘

Общая процедура поиска параметров эквивалентной схемы трансформатора состоит в том, чтобы связать параметры вторичной стороны с параметры первичной стороны или первичной стороны к вторичной стороне.

Итак, перенеся параметры вторичной обмотки на первичную получаем,

R ₂ ^‘ = R ₂ / K ²

X ₂ ^‘ = X ₂ / K ²

Z ₂ ^‘ = Z ₂ / K ²

в то время как

E ₂ ^‘ = E ₂ / K

I ₂ ^‘ = KI ₂

Где,

K = N ₂ / N ₁

Аналогичным образом параметры первичной обмотки могут быть переданы на вторичную сторону и мы можем получить параметры эквивалентной схемы, относящиеся к вторичной обмотке.

R ₁ ^‘ = R ₁ * K ²

X ₁ ^‘ = X ₁ * K ²

Z ₁ ^‘ = Z ₁ * K ²

while,

E ₁ ^‘ = K * E ₁

I ₁ ^‘ = I ₁ / K

I _o ^‘ = I _o / K

Где

K = N ₂ / N ₁

Правила запоминания эквивалентной схемы трансформатора

При передаче параметров помните правило:

Обмотка низкого напряжения => Высокий ток => Низкое сопротивление

Обмотка высокого напряжения => Низкий ток => Высокое сопротивление

Теперь, пока нет- загрузить филиал, который h также известен как возбуждающая цепь между Z ₁ и Z ₂ ^‘ или Z ₂ и Z ₁ ^‘ импедансы не могут быть объединены, и дальнейшее упрощение схемы не может быть выполнено .Итак, происходит процесс приближения, благодаря которому можно найти дальнейшее упрощение или эквивалентность схемы.

Чтобы получить дальнейшее приближение, первым шагом является смещение схемы возбуждения за R ₁ и X ₁ , из-за чего I _o игнорируется, из-за чего такая эквивалентная схема известна как приблизительная эквивалентная схема . Теперь параметры схемы могут быть объединены, такие как R ₁ и R ₂ ^‘, для эквивалентного сопротивления, относящегося к первичному R _1e , и реактивные сопротивления могут быть объединены, такие как X ₁ и X ₂ ^‘ – эквивалентное реактивное сопротивление относительно первичной обмотки X _1e , поэтому полное сопротивление относительно первичной стороны становится равным Z _1e .

Итак, мы можем записать их отношения как

R _1e = R ₁ + R ₂ ^‘ = R ₁ + (R ₂ / K ² )

X _1e = X ₁ + X ₂ ^‘ = X ₁ + (X ₂ / K ² )

Z _1e = R _e + jX _1e

И его величина составляет Z _1e = (R _1e ² + X _1e ² ) ^1/2

And

R _o = V ₁ / I _c

Xo = V ₁ / I _м

Где

I _м = I _o sinϕ _o 900 I77

_c = I _o cosϕ _o

Аналогично соотношение нс для вторичной примерной эквивалентной схемы:

R _2e = R ₂ + R ₁ ^‘ = ₂ + ( _{R 1} * K ² )

X _2e = X ₂ + X ₁ ^‘ = X ₂ + (X ₁ * K ² )

Z _2e = R _2e + jX _2e

И его величина составляет Z _2e = (R _2e ² + X _2e ² ) ^1/2

И

R _o ^‘ = V ₁ ^‘ / I _c ^‘

Xo ^‘ = V ₁ ^‘ / I _m ^‘

Параметры вторичной обмотки для приблизительного эквивалентная схема используются для нахождения примерного напряжения падение в трансформатор.

Связанные темы;

1. Все о трансформаторе
2. КПД и потери трансформатора
3. Характеристики идеального трансформатора
4. Трехфазный трансформатор
5. Испытание трансформатора на обрыв и короткое замыкание Схема эквивалента

   трансформатора

   Эквивалентная схема любого устройства может быть весьма полезной для предопределения поведения устройства в различных условиях эксплуатации, и ее можно нарисовать, если известны уравнения, описывающие его поведение.Если какое-либо электрическое устройство подлежит анализу и дальнейшему исследованию на предмет подходящих модификаций, необходима соответствующая эквивалентная схема.

   Эквивалентная схема для электромагнитных устройств состоит из комбинации сопротивлений, индуктивностей, емкостей, напряжения и т. Д. Таким образом, такая эквивалентная схема (или модель схемы) может быть легко проанализирована и изучена путем прямого применения теории электрических цепей.

   Как указано выше, эквивалентная схема – это просто схемное представление уравнений, описывающих производительность устройства.Поведение трансформатора под нагрузкой и помогает получить эквивалентную схему трансформатора.

   Эквивалентная схема трансформатора с коэффициентом трансформации K = E ₂ / E ₁ показана на рис. 10.17.

   Индуцированная ЭДС в первичной обмотке E ₁ – это приложенное первичное напряжение V ₁ за вычетом падения первичного напряжения. Это напряжение вызывает ток потерь в стали I ₀ и ток намагничивания I _m , и, следовательно, мы можем представить эти две составляющие тока холостого хода током, потребляемым неиндуктивным сопротивлением R ₀ и чистым реактивным сопротивлением X ₀ с приложенным к ним напряжением E ₁ или (V ₁ – первичное падение напряжения), как показано на рис.10.17.

   Вторичный ток, I ₁ = I ’ ₁ / K = I ₁ – I ₀ / K

   Напряжение на клеммах В ₂ на нагрузке индуцируется ЭДС E ₂ во вторичной обмотке за вычетом падения напряжения во вторичной обмотке.

   Эквивалентную схему можно упростить, перенеся напряжение, ток и полное сопротивление на первичную обмотку. После передачи вторичного напряжения, тока и импеданса в эквивалентную схему первичной стороны уменьшаются до значений, показанных на рис.10.18.

   Эквивалентную принципиальную схему можно дополнительно упростить, перенеся сопротивление R ₀ и реактивное сопротивление X ₀ к левому концу, как показано на рис. 10.19. Ошибка, вызванная этим, очень мала, и ею можно пренебречь.

   Ток холостого хода I ₀ едва ли составляет 3-5 процентов от номинального тока полной нагрузки, параллельная ветвь, состоящая из сопротивления R ₀ и реактивного сопротивления X ₀ , может быть опущена без внесения каких-либо заметных ошибок в поведение трансформатора под нагрузкой.Такая схема показана на рис. 10.16 (а). Эквивалентная схема, относящаяся к вторичной стороне (без учета тока холостого хода I ₀ ), проиллюстрирована на рис. 10.15 (a).

   Эквивалентное сопротивление и реактивность:

   Две независимые цепи трансформатора можно разделить на эквивалентную схему, чтобы упростить вычисления.

   Пусть сопротивления и реактивное сопротивление первичной и вторичной обмоток равны R ₁ и R ₂ и X ₁ и X ₂ Ом соответственно, а коэффициент трансформации – K.

   Резистивная капля во вторичной обмотке = I ₂ R ₂

   Реактивное падение во вторичной обмотке = I ₂ X ₂

   Падение сопротивления в первичной обмотке = I ₁ R ₁

   Реактивное падение в первичной обмотке = I ₁ X ₁

   Относится к вторичной стороне:

   Поскольку коэффициент трансформации равен K, поэтому падение сопротивления и реактивности первичной обмотки по отношению к вторичной будет K раз, т.е.е., K I ₁ R ₁ и K I ₁ X ₁ соответственно. Если I ₁ подставить равным KI ₂ , то мы получим первичные резистивные и реактивные падения, относящиеся к вторичной, равные K ² I ₂ R ₁ и K ² I ₂ X ₁ соответственно.

   Суммарное падение сопротивления в трансформаторе = K ² I ₂ R ₁ + I ₂ R ₂ = I ₂ (K ² R ₁ + R ₂ ) = Я ₂ Р ₀₂

   Суммарное реактивное падение трансформатора = K ² I ₂ X ₁ + I ₂ X ₂ = I ₂ (K ² X ₁ + X ₂ ) = Я ₂ Х ₀₂

   Термин (K ² R ₁ + R ₂ ) и (K ² X ₁ + X ₂ ) представляет собой эквивалентное сопротивление и реактивное сопротивление соответственно трансформатора, относящегося к вторичной обмотке, и пусть они будут представлены R ₀₂ и X ₀₂ соответственно.Эквивалентная схема, относящаяся к вторичной обмотке, показана на рис. 10.15 (а).

   Из векторной диаграммы [Рис. 10.15 (b)]

   Где V ₂ – вторичное напряжение на клеммах, I ₂ – вторичный ток, отставание от напряжения на клеммах V ₂ на.

   Поскольку член (I ₂ X ₀₂ cos ɸ – I ₂ , R ₀ , sin ɸ) очень мал по сравнению с членом (V ₂ + I ₂ R ₀₂ cos ɸ + I ₂ X ₀₂ sin ɸ), поэтому, пренебрегая первым, мы имеем –

   K V ₁ = V ₂ + I ₂ R ₀₂ cos ɸ + I ₂ X ₀₂ sin ɸ

   Или V ₂ = KV ₁ – I ₂ R ₀₂ cos ɸ – I ₂ X ₀₂ sin ɸ… (10.23)

   Где V ₁ приложено напряжение к первичной обмотке.

   Если нагрузка чисто резистивная, ɸ = 0 и V ₂ = KV ₁ – I ₂ R ₀₂ … (10.