Выбор труб для теплого пола
Содержание
- 1 Медные трубы
- 2 Металлопластиковые трубы
- 3 Полиэтиленовые трубы
Теплые водяные полы – это удобный и недорогой способ обогрева дома или квартиры. При этом наиболее надежны и экономичны теплые водяные полы, подключенные к системе отопления или отдельному отопительному контуру с питанием от котла. Затраты при выполнении такого пола вполне оправданы, ведь в процессе эксплуатации они окупаются очень быстро. При этом значительную часть затрат составляют затраты на трубы для выполнения греющего контура.
Выбор труб для теплого пола
Какие трубы лучше для теплого пола? Это зависит от нескольких факторов: от способа укладки, длины контура, способа выполнения стяжки и финишного покрытия. Существует несколько видов применяемых труб:
- Медные;
- Металлопластиковые;
- Трубы из сшитого полиэтилена.
Все они имеют свои особенности, которые необходимо учесть при выборе.
Медные трубы
Их отличает высокое качество, отличная теплоотдача, прочность и долговечность, но при этом максимальная из возможных вариантов цена и некоторая сложность в монтаже: гибку труб необходимо производить по шаблону, а для стыков использовать сварку. Кроме того, если греющий контуртеплого пола подключен к системе отопления с алюминиевыми или стальными радиаторами, возможно возникновение гальванической пары, что приведет к электрохимической коррозии радиаторов.
Кроме того, если греющий контуртеплого пола подключен к системе отопления с алюминиевыми или стальными радиаторами, возможно возникновение гальванической пары, что приведет к электрохимической коррозии радиаторов.
Медные трубы для теплого пола
Медные трубы для теплого пола применяют обычно там, где требуется максимально быстрый прогрев помещения при минимальных тепловых потерях. Это актуально для домов, в которых ввиду невозможности установки газового котла теплоноситель получают более дорогостоящим способом: с помощью дизельного или электрического котла. Затраты на медные трубы в 5-7 раз выше, чем на металлопластиковые или полиэтиленовые. При этом температуру теплоносителя для медных труб можно поддерживать на 5-10 градусов меньше, что в конечном итоге приведет к их окупаемости в течение двух-трех лет.
Для теплого пола применяют медные трубы диаметром 20 мм, стараясь сделать минимальное количество стыков. Из-за высокой теплоотдачи температура в начальной части контура может быть значительно выше, чем в конце, из-за чего пол прогревается неравномерно в разных зонах.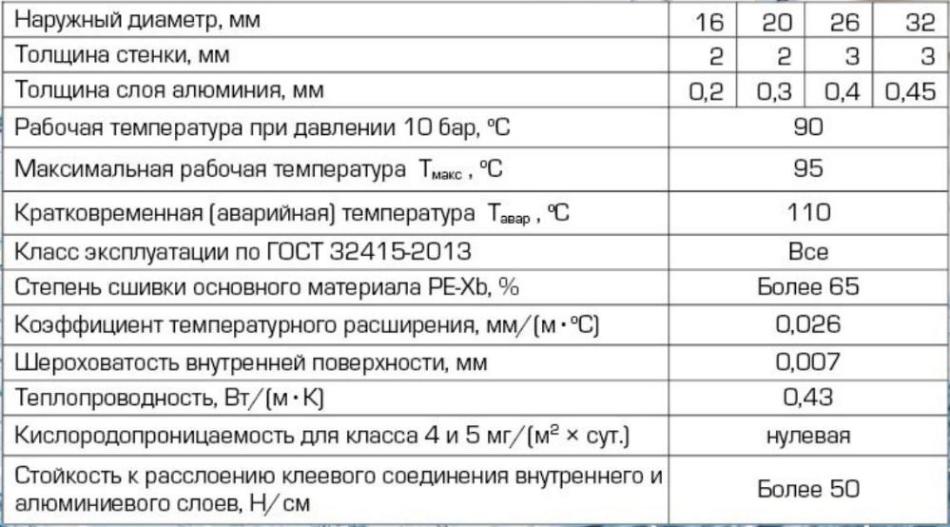 Поэтому предпочтительнее укладывать медные трубы «улиткой» или «двойной змейкой», чтобы рядом проходили как прямая, так и обратная части контура.
Поэтому предпочтительнее укладывать медные трубы «улиткой» или «двойной змейкой», чтобы рядом проходили как прямая, так и обратная части контура.
Укладка труб на пол методом змейки и методом улитки
Металлопластиковые трубы
Металлопластиковые трубы состоят из термостойкого пластика, армированного сплошным или сетчатым металлическим слоем. Их внутренняя поверхность гладкая, на ней не образуется отложений, что позволяет сохранить постоянный рабочий просвет в течение всего срока службы. Для теплого пола необходимо выбирать трубы, предназначенные именно для горячего теплоносителя.
Структура металлопластиковой трубы
Металлопластиковые трубы для теплого пола – самый простой вариант для самостоятельного монтажа. Присоединение греющего контура к прямому и обратному коллектору производится с помощью обжимных фитингов без применения специального инструмента, к тому же трубы при гибке сохраняют форму, и их можно укладывать силами одного человека. При этом металлопластиковые трубы имеют два существенных недостатка:
- фитинги в процессе эксплуатации требуют периодической затяжки, поэтому необходимо обеспечить беспрепятственный к ним доступ;
- при выполнении стяжки нужно следить, чтобы не смять трубы и не сузить их просвет.

Теплоотдача у металлопластиковых труб несколько ниже, чем умедных, однако это компенсируется их невысокой стоимостью и удобством монтажа. Наиболее удобно монтировать металлопластиковые трубы на специальные теплоизолирующие маты с бобышками – их просто укладывают в промежутки между бобышками, создавая необходимый контур, а поверх заливают бетонную стяжку. При таком способе укладки вероятность их повреждения минимальна.
Укладка труб на специальные теплоизолирующие маты
При выборе производителя металлопластиковых труб лучше отдать предпочтение проверенным фирмам, а сами трубы выбрать с кислородонепроницаемым слоем – это продлит срок службы стальных элементов греющего контура. Диаметр труб для греющего контура – 20 мм.
Полиэтиленовые трубы
Один из самых популярных видов выполнения теплого пола подразумевает использование труб из шитого полиэтилена. Эти трубы наиболее дешевые, легко монтируются, обладают упругостью и не боятся сминания при выполнении стяжки. Теплоотдача у полиэтилена ниже, чем у медных или металлопластиковых труб, при этом однослойная структура обладает высокой надежностью. Также стоит остановить на них свой выбор в случае использования в качестве теплоносителя антифризов – полиэтилен обладает очень высокой устойчивостью к агрессивным жидкостям. Еще одним достоинством полиэтиленовых труб является минимальный радиус изгиба, что позволяет выполнить контур любой формы без образования участков с напряжением материала.
Теплоотдача у полиэтилена ниже, чем у медных или металлопластиковых труб, при этом однослойная структура обладает высокой надежностью. Также стоит остановить на них свой выбор в случае использования в качестве теплоносителя антифризов – полиэтилен обладает очень высокой устойчивостью к агрессивным жидкостям. Еще одним достоинством полиэтиленовых труб является минимальный радиус изгиба, что позволяет выполнить контур любой формы без образования участков с напряжением материала.
Комплект полиэтиленовых труб
Наиболее распространенным способом укладки полиэтиленовых труб является подвязка их хомутами к арматурной сетке – трубы эти упруги, не держат форму, и укладка их в определенный контур без закрепления невозможна. Как правило, их применяют под бетонную стяжку, однако возможна и укладка полиэтиленовых труб в специальные теплораспределительные пластины. Контур не должен содержать соединений – именно в местах стыков чаще всего происходят повреждения. Качественные полиэтиленовые трубы должны выдерживать давление не менее 6 бар, температуру теплоносителя не менее 90°С с пиковым повышением до 100-110°С. Также полиэтиленовые трубы должны обладать антикислородным барьером, особенно при подключении теплого пола к системам отопления с использованием стальных и алюминиевых радиаторов. Диаметр для полиэтиленовых труб теплого пола обычно выбирают 16-20 мм, толщину стенки – 2 мм.
Также полиэтиленовые трубы должны обладать антикислородным барьером, особенно при подключении теплого пола к системам отопления с использованием стальных и алюминиевых радиаторов. Диаметр для полиэтиленовых труб теплого пола обычно выбирают 16-20 мм, толщину стенки – 2 мм.
Схема укладки труб для туплого пола
Выбирая производителя медных, металлопластиковых или полиэтиленовых труб, следует обратить внимание на заявленные технические характеристики и гарантийный срок – для всех видов труб он должен быть не менее 10 лет. Срок эксплуатации при отсутствии резких скачков температуры и гидроударов, как правило, составляет не менее 25 лет, что позволит создать комфорт в вашем доме на долгие годы.
как рассчитать длину, сколько метров уходит трубы для водяного пола, как посчитать количество, сколько надо
Содержание:
Выбор труб для теплого пола по материалу изготовления
Способы расчета трубы для пола с обогревом
Проведение вычислений по формуле
Выполнение расчетов на основании схемы
Использование специальных программ
Причиной обустройства системы «теплый пол» чаще всего является недостаточное количество тепловой энергии, поступающей от других отопительных приборов. Перед тем, как приступить к монтажу напольного покрытия с обогревом, следует выполнить некоторые расчеты. В том числе требуется узнать, сколько метров трубы надо на теплый пол.
Перед тем, как приступить к монтажу напольного покрытия с обогревом, следует выполнить некоторые расчеты. В том числе требуется узнать, сколько метров трубы надо на теплый пол.
Чтобы такая система соответствовала своему функциональному назначению, нужно выполнить расчеты максимально точно. Доверить это лучше специалистам, но можно узнать, сколько уходит трубы на теплый пол самостоятельно, если ознакомиться с соответствующей информацией.
Выбор труб для теплого пола по материалу изготовления
Для монтажа пола с обогревом используют трубы из:
- Полипропилена или сшитого полиэтилена. Такие изделия не имеют большую гибкость, которая необходима для прокладки системы, и не обладают достаточной степенью теплоотдачи, поэтому им отдают предпочтение при ограниченных финансовых возможностях.
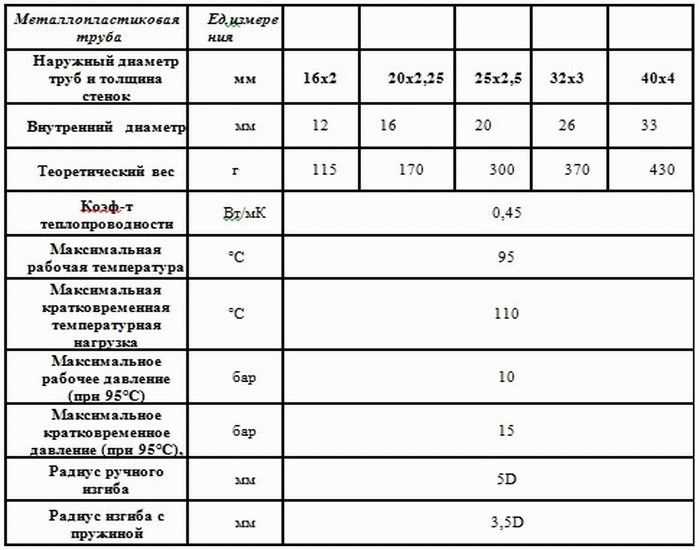
- Металлопластика. Изготавливают такие трубы из прочного пластика. С наружной стороны изделие имеет армирование из алюминия, что способствует повышенной теплоотдаче.
 Цены на металлопластиковую продукцию выше, чем на трубы из пластика. Отличаются изделия из данного материала повышенным коэффициентом теплоотдачи, поэтому они получили широкое применение.
Цены на металлопластиковую продукцию выше, чем на трубы из пластика. Отличаются изделия из данного материала повышенным коэффициентом теплоотдачи, поэтому они получили широкое применение. - Меди. Трубы отличаются высокой степенью теплопроводности, но при этом они плохо гнутся и их стоимость достаточно высокая.
- Нержавейки. Гофрированная трубная продукция из данного материала стоит немного дороже, чем металлопластиковые трубы, но считается самым современным и оптимальным выбором, поскольку у нее очень высокий уровень теплопроводности.
Принимая решение, какие приобрести изделия, следует обращать внимание на их гибкость и коэффициент отдачи тепла, которые влияют на расчет количества трубы для теплого пола. С учетом изложенных требований, специалисты советуют отдавать предпочтение металлопластиковой или гофрированной продукции.
Способы расчета трубы для пола с обогревом
Имеется несколько вариантов, как рассчитать длину труб для теплого пола:
- воспользовавшись формулой;
- на основании протяженности трубопровода, изображенного на схеме;
- применяя онлайн калькулятор или компьютерную программу.

Проведение вычислений по формуле
Расчет длины трубы для теплого пола выполняют, пользуясь формулой:
L = S/N*1,1 + P
где:
L – протяженность трубопровода;
N – расстояние между витками труб в месте поворотов;
1,1 — коэффициент теплопотерь, который является стандартным параметром для всех видов труб и схем укладки;
Р – расстояние между началом пола и отопительным прибором плюс протяженность обратного пути в метрах, его измеряют при помощи рулетки.
Чтобы определить площадь помещения (S), ее длину умножают на ширину. Потом необходимо узнать квадратуру поверхности, на которой планируется монтаж системы обогрева.
Для этого, перед тем, как рассчитать трубу для теплого пола:
- От величины площади комнаты вычитают площадь, которую занимает крупная мебель. Определяют ее на основании размеров предметов обстановки, перемножив их длину и ширину.

- Также нужно уменьшить величину поверхности на площадь промежутка, который требуется для прокладки демпферной ленты, а это отступление от стен комнаты, равное 20-30 сантиметрам.
Для определения N – шага монтажа трубопровода, от которого зависит равномерность прогрева напольного покрытия, пользуются определенными правилами:
- Промежуток между соседними витками, составляющими систему обогрева, может составлять от 10 до 30 сантиметров;
- Подбирать шаг нужно в зависимости от материала изготовления труб (подробнее: “Какое расстояние между трубами теплого пола нужно делать – советы по монтажу”). При этом для труб, характеризующихся меньшей степенью теплоотдачи, расстояние нужно сократить.
- Прокладку системы можно выполнять как с разной величиной шага, так и с одинаковым расстоянием между трубами. Специалисты рекомендуют данный параметр уменьшать в зоне расположения дверей, окон и внешних стен.

В свое время специалистами было вычислено, сколько труб надо для теплого пола при определенном размере шага. Например, при шаге, равном 100 миллиметров, расход труб на один «квадрат» площади составит 10 погонных метров. А при промежутке между витками в 300 миллиметров – 3,4 погонных метра.
Выполнение расчетов на основании схемы
Чтобы определить нужное количество труб, можно пользоваться другим способом, для чего потребуется:
- Подготовить или выбрать схему, согласно которой будет выполняться монтаж трубопровода.
- План с конкретным шагом укладки нанести на миллиметровую бумагу.
- При нанесении чертежа следует соблюдать масштаб.
До того как посчитать трубу на теплый пол, нужно подобрать вариант укладки, который может иметь вид:
- одинарной змейки – трубопровод после вхождения в комнату, принимает форму синусоиды.
 Данный способ оптимален для небольших по площади помещений с контуром малой протяженности;
Данный способ оптимален для небольших по площади помещений с контуром малой протяженности; - двойной змейки – трубы в данном случае укладывают попеременно, что позволяет выровнять температуру напольного покрытия по всей его площади;
- улитки – нагревательный контур располагают по спирали, благодаря чему пол по периметру прогревается с одинаковой теплоотдачей.
Использование специальных программ
Еще одним способом расчета трубы для теплого пола является применение:
- так называемых онлайн калькуляторов, которые имеются на сайтах в интернете. Они позволят быстро узнать требуемый результат;
- специализированных программ, таких, как VALTEC, SketchUP или других продуктов. В отличие от онлайн калькулятора они способны в более полном объеме высчитать требуемый результат с учетом разных вводных параметров.
Чтобы выполнить расчет труб для теплого водяного пола при помощи программы или калькулятора, нужно располагать конкретными данными:
- размеры помещения;
- вид труб;
- схема прокладки;
- шаг укладки;
- толщина материала для покрытия (бетонной стяжки, ламината, ковролина и т.
 д.).
д.).
Некоторыми специальными программными продуктами можно пользоваться бесплатно, а за другие нужно платить.
Правильно произведенные расчеты позволяют смонтировать пол с подогревом с минимальными финансовыми затратами.
Теплопроводность пластика и металла I. — Сборник экспериментов
Номер эксперимента: 1764
Цель эксперимента
В этом эксперименте мы визуализируем нагрев металлической и пластиковой пластины; цель состоит в том, чтобы подчеркнуть различную теплопроводность этих материалов.
Теория
Теплопередача за счет теплопроводности особенно характерна для твердых тел; он почти не проявляется в жидкостях и газах. В случае неэлектропроводных материалов перенос тепла можно объяснить тем, что частицы в нагретой части тела колеблются и передают часть своей кинетической энергии соседним частицам.
 В электропроводных материалах за теплопроводность в основном отвечают свободные электроны.
В электропроводных материалах за теплопроводность в основном отвечают свободные электроны.Величина, которая описывает способность вещества проводить тепло, называется теплопроводностью λ , [ λ ] = Вт·м −1 ·K −1 , и слабо зависит от температуры . Для очень хороших теплопроводников (металлов) она находится в пределах от десятков до сотен ватт на метр на кельвин, теплопроводность лучших теплоизоляторов (некоторые пластмассы или воздух) составляет около 0,02-0,05 Вт·м −1 ·К −1 .
Инструменты
Тепловизор, металлическая и пластиковая пластина примерно одинаковых размеров (примерно с человеческую ладонь). Металлическая пластина должна быть покрыта матовым покрытием.
Процедура
Положите одну руку на металл, а другую руку на пластиковую пластину. Наблюдайте за обеими пластинами с помощью тепловизионной камеры в течение 20 секунд. В то время как металлическая пластина за это время почти равномерно прогревается, температура пластиковой пластины повышается только в месте контакта с ладонью — пластик является изолятором и не позволяет теплу распределяться по периферийным частям пластины.

Пример результата
Успешно проведенный эксперимент показан на видео ниже. Металлическая пластина всегда справа, пластиковая пластина слева.
При съемке видео использовалась тепловизионная камера FLIR i7. Температурный диапазон цветовой схемы выбран в интервале от 22°С до 34°С, коэффициент излучения ε = 0,95.
Технические примечания
В этом эксперименте пластиковая пластина была вырезана из полипропиленовой офисной папки; металлическая пластина вырезана из алюминиевого листа толщиной 0,5 мм.
При проведении эксперимента с тепловизором необходимо, чтобы исследуемые объекты имели одинаковую излучательную способность, чтобы они «отражали одинаково». Большинство тепловизионных камер настроены на коэффициент излучения ε = 0,95, что соответствует очень малой отражающей поверхности.

Педагогические примечания
Постепенное изменение цвета нагретых поверхностей может привести к частому ошибочному толкованию того, что некоторые из пластин содержат на больше тепла, чем другие. Это неправильное представление о тепле как о переменной состояния. Поэтому необходимо подчеркнуть, что то, что мы видим на термограмме, есть распределение температуры (!) , а не распределение тепла, которое описывает только обмен энергией.
Проведение эксперимента без тепловизора
Тепловизионная камера — очень дорогой инструмент, но эксперимент можно провести с гораздо более доступной термочувствительной пленкой, которую можно найти под названием с реверсивной температурной этикеткой . Поместите термочувствительную пленку под пластиковую и металлическую пластину (см.
 рис. 1). Таким образом, нет необходимости покрывать блестящие поверхности матовым покрытием.
рис. 1). Таким образом, нет необходимости покрывать блестящие поверхности матовым покрытием.В данном эксперименте использовалась термочувствительная пленка, работающая в диапазоне температур от 25°С до 30°С. При комнатной температуре (около 22 °C) пленка черная; при нагревании выше 25 °C он меняет цвет с коричневого на зеленый. Результат эксперимента с термочувствительной пленкой показан на рис. 2 (металлическая пластина справа, пластик слева). В то время как термочувствительная пленка под пластиковой пластиной показывает очертания ладони, пленка под металлической пластиной показывает, что пластина нагревается равномерно.
Кондуктивный теплообмен | Инженерная библиотека
На этой странице представлена глава о кондуктивной теплопередаче из «Справочника по основам DOE: термодинамика, теплопередача и поток жидкости», DOE-HDBK-1012/2-92, Министерство энергетики США, июнь 1992 г.
Другие связанные главы из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости» можно увидеть справа.
Кондуктивный теплообмен — это передача тепловой энергии за счет взаимодействий между соседними атомами и молекулами твердого тела.
Проводка
Теплопроводность включает передачу тепла за счет взаимодействия между соседними молекулами материала. Теплопередача за счет теплопроводности зависит от движущей «силы» разницы температур и сопротивления теплопередаче. Сопротивление теплопередаче зависит от природы и размеров теплоносителя. Все проблемы теплообмена связаны с разностью температур, геометрией и физическими свойствами изучаемого объекта.
В задачах о кондуктивном теплообмене объектом исследования обычно является твердое тело. Проблемы конвекции связаны с жидкой средой. Проблемы теплопередачи излучением связаны с твердыми или жидкими поверхностями, разделенными газом, паром или вакуумом. Существует несколько способов соотнести геометрию, физические свойства и разность температур объекта со скоростью теплопередачи через объект. В кондуктивной теплопередаче наиболее распространенным средством корреляции является закон проводимости Фурье. Закон в форме уравнения чаще всего используется в прямоугольной или цилиндрической форме (трубы и цилиндры), обе из которых представлены ниже.
Закон в форме уравнения чаще всего используется в прямоугольной или цилиндрической форме (трубы и цилиндры), обе из которых представлены ниже.
| Прямоугольный | $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$ |
(2-4)
| Цилиндрический | $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$ |
(2-5)
куда:
| \( \ точка {Q} \) | = | скорость теплопередачи (БТЕ/ч) |
| А | = | площадь поперечного сечения теплопередачи (фут 2 ) |
| Δx | = | толщина плиты (футы) |
| Δr | = | толщина цилиндрической стенки (футы) |
| ΔТ | = | разница температур (°F) |
| к | = | теплопроводность плиты (БТЕ/фут-час-°F) |
Использование уравнений 2-4 и 2-5 для определения количества тепла, передаваемого теплопроводностью, продемонстрировано в следующих примерах.
Прямоугольные координаты проводимости
Пример:
1000 БТЕ/час проходит через участок изоляционного материала, показанный на рисунке 1, площадь поперечного сечения которого составляет 1 фут 2 . Толщина 1 дюйм, теплопроводность 0,12 БТЕ/час-фут-°F. Вычислите разницу температур по всему материалу.
Рисунок 1: Проводимость через плитуРешение:
Используя уравнение 2-4:
$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$ 9{\ circ} F \end{эквнаррай} $$
Пример:
Бетонный пол с проводимостью 0,8 БТЕ/час-фут-°F имеет размеры 30 футов на 40 футов и толщину 4 дюйма. Пол имеет температуру поверхности 70°F, а температура под ним 60°F. Каков тепловой поток и скорость теплопередачи через пол?
Решение:
Используя уравнения 2-1 и 2-4:
$$
\begin{выравнивание}
\dot{Q}” &=& { \dot{Q} \over A } = k \left({ \Delta T \over \Delta x }\right) \nonumber \\
&=& \left({ 0.8 ~{\text{Btu} \over \text{hr-ft-}^{\circ}\text{F}} }\right) \left({ 10^{\circ} \text{F} \over 0. 2 }
\end{эквнаррай}
$$ 92) \номер\\
&=& 28 800 ~{\text{Btu} \over \text{hr}}
\end{эквнаррай}
$$
2 }
\end{эквнаррай}
$$ 92) \номер\\
&=& 28 800 ~{\text{Btu} \over \text{hr}}
\end{эквнаррай}
$$
Метод эквивалентного сопротивления
Теплопередачу можно сравнить с протеканием тока в электрических цепях. Скорость теплопередачи можно рассматривать как ток, а комбинацию теплопроводности, толщины материала и площади как сопротивление этому потоку. Разность температур представляет собой потенциальную или движущую функцию для теплового потока, в результате чего уравнение Фурье записывается в форме, аналогичной закону Ома теории электрических цепей. Если член теплового сопротивления Δx/k записать как член сопротивления, где сопротивление является обратной величиной теплопроводности, деленной на толщину материала, результатом будет уравнение проводимости, аналогичное электрическим системам или сетям. Электрическая аналогия может использоваться для решения сложных задач, связанных как с последовательными, так и с параллельными тепловыми сопротивлениями. Ученик обращается к рисунку 2, на котором показана схема эквивалентного сопротивления. Типичная задача проводимости в ее аналогичной электрической форме дается в следующем примере, где «электрическое» уравнение Фурье может быть записано следующим образом.
Типичная задача проводимости в ее аналогичной электрической форме дается в следующем примере, где «электрическое» уравнение Фурье может быть записано следующим образом.
$$ \dot{Q}” = { \Delta T \over R_{th} } $$
(2-6)
куда:
| \(\точка{Q}”\) | = | Тепловой поток (\( \dot{Q}/A \)) (Btu/hr-ft 2 ) |
| ΔТ | = | Разница температур (°F) |
| Р й | = | Термическое сопротивление (Δx/k) (час-фут 2 -°F/Btu) |
Электрическая аналогия
Пример:
Композитная защитная стена состоит из медной пластины толщиной 1 дюйм, слоя асбеста толщиной 1/8 дюйма и слоя стекловолокна толщиной 2 дюйма. Теплопроводность материалов в единицах БТЕ/час-фут-°F следующая: k Cu = 240, k asb = 0,048 и k fib = 0,022. Общая разница температур по всей стене составляет 500°F. Рассчитайте термическое сопротивление каждого слоя стены и скорость теплопередачи на единицу площади (тепловой поток) через композитную конструкцию.
92}
\end{эквнаррай}
$$
Общая разница температур по всей стене составляет 500°F. Рассчитайте термическое сопротивление каждого слоя стены и скорость теплопередачи на единицу площади (тепловой поток) через композитную конструкцию.
92}
\end{эквнаррай}
$$
Кондуктивные цилиндрические координаты
Теплопередача через прямоугольное твердое тело является наиболее прямым применением закона Фурье. Теплопередачу через трубу или стенку трубы теплообменника оценить сложнее. Через цилиндрическую стенку площадь поверхности теплопередачи постоянно увеличивается или уменьшается. Фиг.3 представляет собой сечение трубы, изготовленной из однородного материала.
Рисунок 3: Площадь поперечного сечения цилиндрической трубыПлощадь поверхности (A) для передачи тепла по трубе (без учета концов трубы) прямо пропорциональна радиусу (r) трубы и длине (L) трубы.
А = 2πrL
По мере увеличения радиуса от внутренней стенки к внешней увеличивается площадь теплообмена.
Разработка уравнения, оценивающего теплопередачу через объект цилиндрической геометрии, начинается с закона Фурье (уравнение 2-5).
$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$
Из приведенного выше обсуждения видно, что никакое простое выражение для площади не является точным. Ни площадь внутренней поверхности, ни площадь внешней поверхности сами по себе не могут использоваться в уравнении. Для задачи с цилиндрической геометрией необходимо определить среднелогарифмическую площадь поперечного сечения (A lm ).
$$ A_{lm} = { A_{внешний} – A_{внутренний} \over \ln \left({ A_{внешний} \over A_{внутренний} }\right) } $$
(2-7)
Подстановка выражения 2πrL для площади в уравнении 2-7 позволяет вычислить среднелогарифмическую площадь по внутреннему и внешнему радиусу без предварительного вычисления внутренней и внешней площади.
$$ \begin{выравнивание} A_{lm} &=& { 2 \pi ~r_{внешняя} L – 2 \pi ~r_{внутренняя} L \over \ln \left({ 2 \pi ~r_{внешняя} L \over 2 \pi ~ r_{внутренний} L }\right) } \nonumber \\ &=& 2 \pi ~L \left({ r_{внешний} – r_{внутренний} \over \ln{ r_{внешний} \over r_{внутренний} } }\right) \end{эквнаррай} $$
Это выражение для логарифмической средней площади можно подставить в уравнение 2-5, что позволит нам рассчитать скорость теплопередачи для цилиндрических геометрий.
$$ \begin{выравнивание} \dot{Q} &=& k ~A_{lm} \left({ \Delta T \over \Delta r }\right) \nonumber \\ &=& k \left[ 2 \pi ~L \left({ r_o – r_i \over \ln{ r_o \over r_i } }\right) \right] \left({ T_o – T_i \over r_o – r_i }\ справа) \номер\\ \dot{Q} &=& { 2 \pi ~k ~L ~(\Delta T) \over \ln (r_o / r_i) } \end{эквнаррай} $$
(2-8)
куда:
| Л | = | длина трубы (фут) |
| р я | = | внутренний радиус трубы (футы) |
| р или | = | внешний радиус трубы (футы) |
Пример:
Труба из нержавеющей стали длиной 35 футов имеет внутренний диаметр 0,92 фута и внешний диаметр 1,08 фута. Температура внутренней поверхности трубы составляет 122°F, а температура внешней поверхности составляет 118°F. Теплопроводность нержавеющей стали составляет 108 БТЕ/час-фут-°F. 92 } \end{эквнаррай} $$
Пример:
Труба длиной 10 футов с внутренним радиусом 1 дюйм и внешним радиусом 1,25 дюйма имеет температуру внешней поверхности 250°F.


 Цены на металлопластиковую продукцию выше, чем на трубы из пластика. Отличаются изделия из данного материала повышенным коэффициентом теплоотдачи, поэтому они получили широкое применение.
Цены на металлопластиковую продукцию выше, чем на трубы из пластика. Отличаются изделия из данного материала повышенным коэффициентом теплоотдачи, поэтому они получили широкое применение.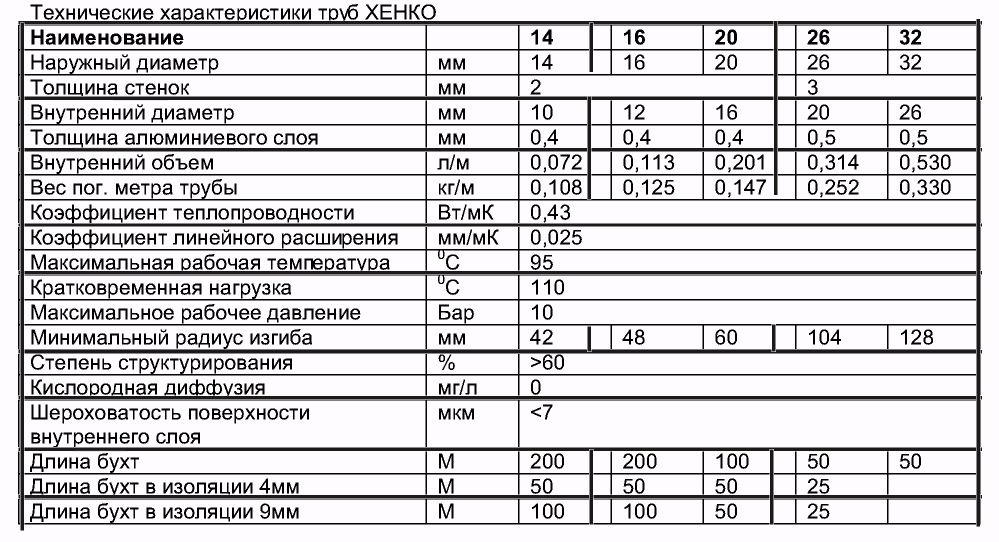


 Данный способ оптимален для небольших по площади помещений с контуром малой протяженности;
Данный способ оптимален для небольших по площади помещений с контуром малой протяженности; д.).
д.).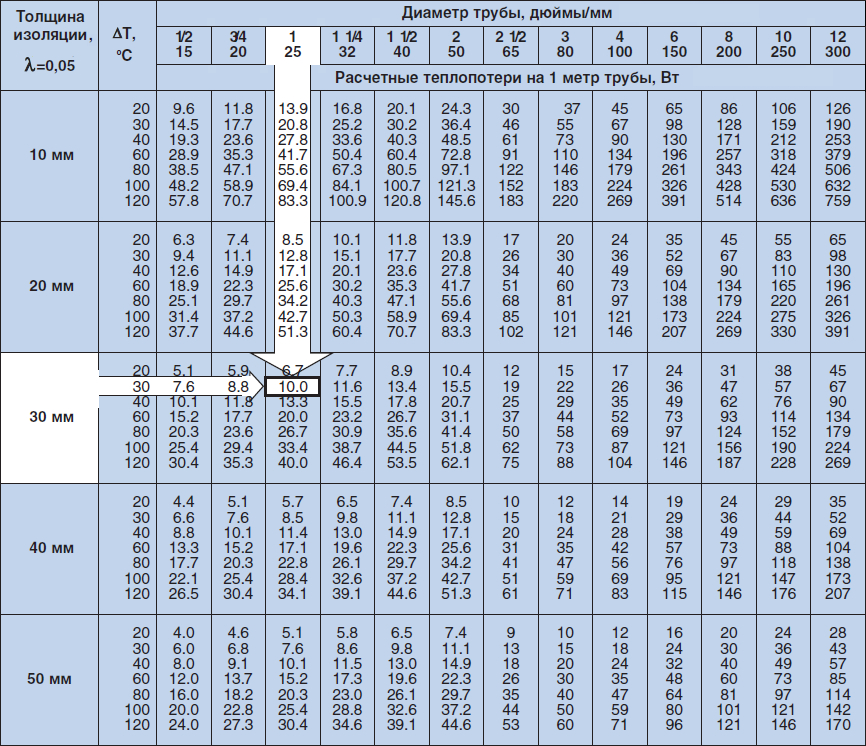 В электропроводных материалах за теплопроводность в основном отвечают свободные электроны.
В электропроводных материалах за теплопроводность в основном отвечают свободные электроны.
 рис. 1). Таким образом, нет необходимости покрывать блестящие поверхности матовым покрытием.
рис. 1). Таким образом, нет необходимости покрывать блестящие поверхности матовым покрытием.