Тепловая энергия: определение, формула и примеры для детей

В предыдущих статьях мы видели, что Кинетическая энергия и механическая энергия. В этих статьях мы упоминали тепловую энергию как часть энергии, которая влияет на рассматриваемое тело и овладевает им. Термальная энергия Это энергия, которой обладают все частицы, составляющие тело. Когда температура колеблется между повышением и понижением, активность тела увеличивается. Эта внутренняя энергия увеличивается при повышении температуры и уменьшается при понижении.

Теперь мы собираемся тщательно проанализировать этот тип энергии и дополнить наши знания о различных существующих типах энергии. Хотите узнать об этом больше? Читайте дальше, и вы узнаете.

Индекс

• 1 Характеристики тепловой энергии
  • 1.1 Примеры тепловой энергии
• 2 Как производится тепловая энергия?
  • 2.1 Как используется тепловая энергия?
• 3 Измерение внутренней энергии
• 4 Примеры тепловой энергии
• 5 Частая путаница
• 6 Другие родственные энергии
  • 6. 1 Тепловая солнечная энергия
  • 6.2 геотермальной энергии
  • 6.3 Электрическая и химическая энергия

Характеристики тепловой энергии

Это энергия, которая вмешивается в различные теплотворные процессы, происходящие при контакте тел с разной температурой. Пока тела поддерживают трение между собой, эта энергия будет передаваться от одного тела к другому. Вот что происходит, например, когда мы кладем руку на поверхность. Спустя некоторое время, поверхность будет иметь температуру руки, потому что он дал это ему.

Прирост или потеря этой внутренней энергии во время процесса это называется теплом. Тепловую энергию получают разными способами. Следовательно, каждое тело, имеющее определенную температуру, имеет внутри внутреннюю энергию.

Примеры тепловой энергии

Рассмотрим подробнее источники получения тепловой энергии:

• Природа и Солнце Это два источника энергии, которые обеспечивают внутреннюю энергию телам. Например, когда утюг постоянно находится на солнце, его температура повышается, потому что он поглощает внутреннюю энергию. К тому же звездный король – ярчайший пример тепловой энергии. Это самый крупный известный источник тепловой энергии. Животные, которые не могут регулировать свою температуру, используют для этого преимущества этого источника энергии.
• Кипящая вода: По мере повышения температуры воды тепловая энергия всей системы начинает умножаться. Пришло время, когда повышение температуры тепловой энергии вынудило воду к фазовому переходу.
• Камины: энергия, производимая в дымоходах, происходит за счет увеличения тепловой энергии. Здесь поддерживается сжигание органических веществ, чтобы в доме было тепло.
• Нагреватель: служит для повышения температуры воды аналогично тому, как мы кипятим.
• Экзотермические реакции которые происходят из-за сжигания некоторого топлива.
• Ядерные реакции что происходит ядерное деление. Это также происходит, когда происходит слияние ядер. Когда два атома имеют одинаковый заряд, они соединяются, образуя более тяжелое ядро, и во время процесса выделяют большое количество энергии.
• Эффект джоуля происходит, когда в проводнике циркулирует электрический ток, и кинетическая энергия электронов преобразуется во внутреннюю энергию в результате непрерывных столкновений.
• Сила трения Он также генерирует внутреннюю энергию, поскольку также происходит обмен энергией между двумя телами, будь то физический или химический процесс.

Как производится тепловая энергия?

Мы должны думать, что энергия не создается и не уничтожается, а только трансформируется. Тепловая энергия вырабатывается разными способами. Он создается движением атомов и молекул материи. как форма кинетической энергии, производимой случайными движениями. Когда система имеет большее количество тепловой энергии, ее атомы движутся быстрее.

Как используется тепловая энергия?

Тепловая энергия может быть преобразована с помощью теплового двигателя или механической работы. Среди наиболее распространенных примеров – двигатель автомобиля, самолета или лодки. Тепловую энергию можно использовать разными способами. Посмотрим, какие из них основные:

• В тех местах, где нужно тепло. Например, как отопление в доме.
• Преобразование механической энергии. Примером этого являются двигатели внутреннего сгорания в автомобилях.
• Преобразование электрической энергии. Это генерируется на тепловых электростанциях.

Измерение внутренней энергии

Внутренняя энергия измеряется согласно Международная система единиц в джоулях (Дж). Он также может быть выражен в калориях (Cal) или килокалориях (Kcal). Чтобы хорошо понять внутреннюю энергию, мы должны помнить принцип сохранения энергии. «Энергия не создается и не уничтожается, она только трансформируется от одного к другому». Это означает, что даже если энергия непрерывно трансформируется, она всегда одинакова.

Кинетическая энергия, которую переносит автомобиль при ударе о здание, направляется прямо в стену. Следовательно, в результате его внутренняя энергия увеличивается, а кинетическая энергия автомобиля уменьшается.

Примеры тепловой энергии

Тепловая или тепловая энергия находится, например, в:

• Теплокровные животные. Например, когда нам холодно, мы обнимаем других. Так мало-помалу мы чувствуем себя лучше, потому что он передает нам свое тепло.
• На металле, подверженном воздействию солнца. Летом особенно загорается.
• Когда мы кладем кубик льда в чашку с горячей водой, мы видим, что он тает, потому что к нему передается тепло.
• Печи, радиаторы и в любом другом система обогрева.

Частая путаница

Очень часто путают тепловую энергию с тепловой. Его часто используют как синонимы, даже если они не имеют к нему никакого отношения. Тепловая энергия сосредоточена исключительно на излучении тепла в его тепловых явлениях. Таким образом, она отличается от тепловой энергии, которая представляет собой только тепло.

Количество тепла в теле – это мера тепловой энергии, в то время как тепло, которое может исходить от тела, указывает на то, что оно обладает более высокой теплоемкостью. Температура тела дает нам ощущение тепла и может дать нам сигнал, который указывает количество имеющейся у него тепловой энергии. Как мы уже говорили, чем выше температура тела, тем больше энергии.

Тепло может передаваться разными способами. Давайте рассмотрим их один за другим:

• Электромагнитное волновое излучение.
• Вождение. Когда энергия передается от более теплого тела к более холодному телу, возникает проводимость. Если тела имеют одинаковую температуру, обмен энергией отсутствует. Тот факт, что два тела равны своей температуре, когда они находятся в контакте, – это еще один физический принцип, называемый тепловым равновесием. Например, когда мы касаемся холодного объекта рукой, тепловая энергия передается этому объекту, вызывая ощущение холода в нашей руке.
• Конвекция. Это происходит, когда самые горячие молекулы переходят из одной стороны в другую. Это происходит в природе постоянно на ветру. Самые горячие частицы имеют тенденцию двигаться туда, где меньше плотность.

Другие родственные энергии

Тепловая энергия связана со многими другими формами энергии. Вот некоторые из них.

Тепловая солнечная энергия

Это тип возобновляемой энергии, состоящий из преобразование солнечной энергии в тепло. Эта энергия используется для нагрева воды в различных целях, например, в быту или в больницах. Он также служит для отопления в зимние дни. Источником является солнце, и оно принимается напрямую.

геотермальной энергии

Получение тепловой энергии оказывает воздействие на окружающую среду из-за к выбросу углекислого газа и радиоактивных отходов. Однако если используется энергия из недр земли. Это также вид возобновляемой энергии, который не загрязняет окружающую среду и не наносит ей ущерба.

Электрическая и химическая энергия

Тепловая энергия может быть преобразована в электрическую. Например, ископаемое топливо генерирует электричество, сжигая и высвобождая его. Электрическая энергия дается как результат разности потенциалов между двумя точками. и позволяет создавать электрический ток между ними, когда они входят в контакт с электрическим проводником. Проводник может быть металлическим.

Тепловая энергия – это тип энергии, высвобождаемой в виде тепла из-за контакта тела с более высокой температурой с другим с более низкой температурой, а также она может быть получена различными способами или способами, как упоминалось ранее. Химическая энергия тот, который имеет химическую связь, то есть это энергия, производимая исключительно химическими реакциями.

Благодаря этой информации вы сможете лучше понять тепловую энергию.

Глава 15. Тепловая энергия и работа: начала термодинамики – FIZI4KA

Физика с формулами ›

В этой главе…

• Достигаем теплового равновесия
• Сохраняем тепловую энергию при различных условиях
• Повышаем эффективность тепловых двигателей
• Падаем почти до абсолютного нуля

Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало).

Итак, самое время обратиться к термодинамике.

Содержание

• Стремимся к тепловому равновесию: нулевое начало термодинамики
• Сохраняем энергию: первое начало термодинамики
  • Применяем закон сохранения энергии
  • Изучаем изобарические, изохорические, изотермические и адиабатические процессы
    • Постоянное давление: изобарический процесс
    • Постоянный объем: изохорический процесс
    • Постоянная температура: изотермический процесс
    • Постоянная энергия: адиабатический процесс
  • Вычисляем удельную теплоемкость
• Передаем тепловую энергию: второе начало термодинамики
  • Заставим тепловую энергию работать: тепловые двигатели
  • Оцениваем эффективность работы: КПД теплового двигателя
  • Как сказал Карно: нельзя все тепло превратить в работу
    • Построение двигателя Карно
    • Используем формулу Карно
• Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Стремимся к тепловому равновесию: нулевое начало термодинамики

Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)

Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)

Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.

Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.

Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.

Сохраняем энергию: первое начало термодинамики

Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ​\( Q \)​, а сама система выполняет над окружающими телами работу ​\( W \)​ (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ​\( U_н \)​, становится равной \( U_к \) следующим образом:

В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.

На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное \( Q \), то при отсутствии работы ее количество внутренней энергии, обозначаемое как \( U \), изменится на \( Q \). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия \( U \) изменится на \( W \). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.

Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.

Применяем закон сохранения энергии

Величина передаваемой тепловой энергии \( Q \) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы \( W \) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.

Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.

Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:

Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:

В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:

а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ​\( W \)​ считается отрицательным. Таким образом, получаем:

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.

В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).

Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.

Постоянное давление: изобарический процесс

Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.

Какую работу выполняет система при расширении газа? Работа равна произведению ​\( F \)​ на ​\( s \)​, означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ​\( P \)​ на ​\( A \)​, означающих, соответственно, давление и площадь. Это значит, что:

Но произведение площади \( A \) и перемещения \( s \) равно изменению объема ​\( \Delta\!V \)​. Таким образом:

Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ​\( W=P\Delta\!V \)​, то работа — это площадь, ограниченная графиком.

Допустим, имеется 60 м³ идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м³ (​\( PV= nRT \)​, где ​\( n \)​, ​\( R \)​ и ​\( Т \)​ означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:

Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.

Постоянный объем: изохорический процесс

А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).

Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ​\( Fs \)​ (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.

Постоянная температура: изотермический процесс

В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как \( PV= nRT \) (см. главу 14), то температура также остается постоянной.

Какая работа выполняется при изменении объема? Поскольку \( PV= nRT \), то получается такое отношение между ​\( P \)​ и ​\( V \)​:

Эту формулу иллюстрирует график, показанный на рис. 15.6.

Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ​\( ln \)​ — натуральный логарифм, ​\( R \)​ — газовая постоянная (8,31), ​\( V_1 \)​ и ​\( V_0 \)​ означают, соответственно, конечный и начальный объем:

Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ​\( (3/2)nRT \)​ (см. главу 14), то эта энергия не меняется. Таким образом:

другими словами:

Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ​\( Q \)​, а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ​\( V_0 \)​ = 0,010 м³ до \( V_1 \)​ = 0,020 м³. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:

Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ​\( Q=W \)​, то добавляемая к газу тепловая энергия также равна 1690 Дж.

Постоянная энергия: адиабатический процесс

При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.

Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ​\( Q \)​ = 0, таким образом:

Так как внутренняя энергия ​\( U \)​ идеального газа равна ​\( (3/2)nRT \)​ (см. главу 14), то выполняется работа:

где ​\( T_0 \)​ и \( T_1 \) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).

Вычисляем удельную теплоемкость

Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:

Что такое ​\( \gamma \)​? Это отношение ​\( C_p/C_v \)​ двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ​\( C_p \)​, а в знаменателе — теплоемкость при постоянном объеме \( C_v \). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ​\( Q \)​, необходимой для изменения температуры тела единичной массы на величину ​\( \Delta T \)​, т.е. ​\( c=Q/m\Delta T \)​, где ​\( c \)​, ​\( m \)​ и \( \Delta T \) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ​\( C \)​ и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ​\( n \)​, а не массой ​\( m \)​:

Как найти ​\( C \)​? Надо вычислить две разные величины: ​\( C_\mathrm{p} \)​ (при постоянном давлении) и \( C_\mathrm{v} \) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ​\( Q=\Delta U+W \)​. Поэтому достаточно только выразить ​\( \Delta U \)​ через ​\( T \)​. Выполняемая работа ​\( W \)​ равна ​\( P\Delta\!V \)​, тогда при постоянном объеме ​\( W \)​ = 0. А изменение внутренней энергии идеального газа равно ​\( (3/2)nR\Delta T \)​ (см. главу 14), поэтому ​\( Q \)​ при постоянном объеме выражается следующей формулой:

При постоянном давлении работа ​\( W \)​ равна \( P\Delta\!V \). А поскольку ​\( PV= nRT \)​, то ​\( W=P(V_1-V_0)=nR(T_1-T_0) \)​. Поэтому ​\( Q \)​ при постоянном давлении выражается следующей формулой:

Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ​\( Q=Cn\Delta T \)​, поэтому \( C=Q/n\Delta T \). {5/3} \)​ оставляем в левой части равенства только \( P_1 \)​ и получаем:

Подставив в эту формулу численные значения, получим:

Итак, новое давление должно быть равно 0,314 атмосферы.

Передаем тепловую энергию: второе начало термодинамики

Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.

Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.

Заставим тепловую энергию работать: тепловые двигатели

Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.

Оцениваем эффективность работы: КПД теплового двигателя

Тепловая энергия, подаваемая нагревателем, обозначается как ​\( Q_{нг} \)​, а отправляемая в холодильник (см. предыдущий раздел) — как ​\( Q_{\mathrm{x}} \)​. Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ​\( W \)​, выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:

Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:

Это значит, что для записи КПД достаточно использовать \( Q_{нг} \) и \( Q_{\mathrm{x}} \):

Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·10⁷ Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ​\( W \)​ = 2,55·10⁷ Дж и

Это значит, что:

Количество входящей тепловой энергии равно 3,27·10⁷ Дж. А сколько тепловой энергии \( Q_{\mathrm{x}} \) остается неизрасходованной и отправляется в холодильник? Как известно:

поэтому:

Подставив в эту формулу численные значения, получим:

Количество тепловой энергии, отправляемое в холодильник, равно 0,72·10⁷ Дж.

Как сказал Карно: нельзя все тепло превратить в работу

Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.

А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.

Построение двигателя Карно

Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ​\( T_{нг} \)​. А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру \( T_{х} \).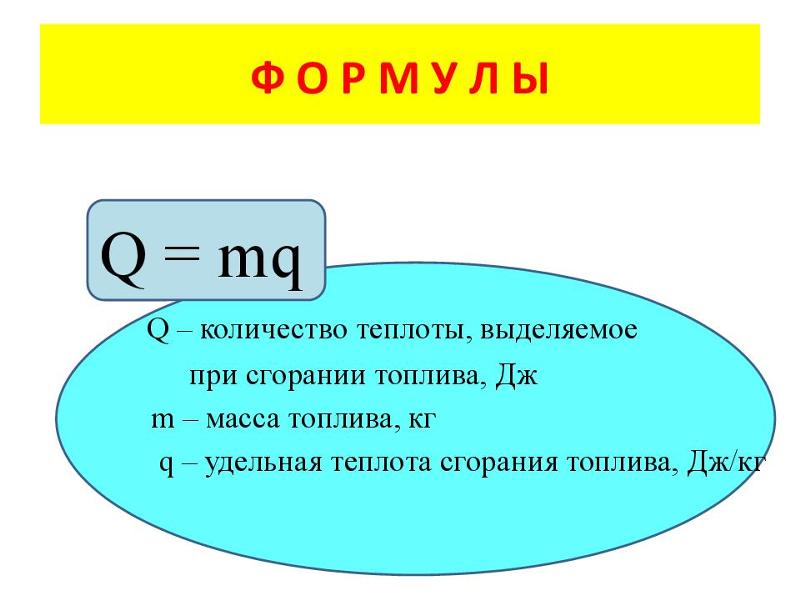 Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):

А так как КПД теплового двигателя вычисляется по следующей формуле:

то получается такая формула для вычисления КПД двигателя Карно:

где температура выражается в кельвинах.

В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. \( T_{х} \) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.

Используем формулу Карно

Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:

Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:

Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.

Странные явления вблизи абсолютного нуля

Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!

(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)

Глава 16. Электризуемся: изучаем статическое электричество →

← Глава 14. Передаем тепловую энергию в твердых телах и газах

Учебное пособие по теплу, температуре и тепловой энергии

Инструменты Creator скоро будут вдохновлять!

Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.

Физика

Общая физика

Теплофизика

Учебное пособие по теплу, температуре и тепловой энергии

Кристалл

HS-PS3-4

Сравнение теплоты и температуры провести непросто, поскольку они близки родственные понятия.

Содержание

ВВЕДЕНИЕ

Что сейчас у тебя под ногами? Ковер? Плитка? Это бетонная дорожка, трава, грязь и листья? Тысячи миль земли под вашими ногами, осознаете вы это или нет, состоят из множества компонентов, включая почву, горные породы, водные реки, вулканическую лаву и твердое железо.

Ядро Земли — это самый внутренний геологический слой планеты, и новые научные исследования заставили специалистов предположить, что температура внутреннего ядра Земли превышает 10 800 F — такая же температура, как и на поверхности Солнца! Но что такое температура? Это то же самое, что и термин «тепло»? Давайте посмотрим.

Источник

ЧТО ТАКОЕ ТЕПЛОВАЯ ЭНЕРГИЯ?

• Энергия, содержащаяся в системе, которая отвечает за ее температуру, является определением тепловой энергии.
• Суммарная кинетическая и потенциальная энергия физической системы называется ее тепловой энергией.
• Всю тепловую энергию часто называют полной внутренней энергией системы.
• Хотя тепло и тепловая энергия часто используются взаимозаменяемо, с научной точки зрения это не одно и то же.
• Движение атомов внутри объекта или системы называется тепловой энергией.
• Все или материалы обладают тепловой энергией, и солнце является крупнейшим источником тепловой энергии в нашей Солнечной системе.

Эту тепловую энергию можно рассчитать по формуле c – удельная теплоемкость, а ΔT – разница температур.

ЧТО ТАКОЕ ТЕПЛО?

• Определение тепла гласит, что это поток тепловой энергии от одного объекта или вещества к другому.
• Любая кастрюля или чайник, которые вы ставите на работающую плиту, вырабатывает тепловую энергию.
• Тепло может передаваться от горелки к кастрюле, которая затем передает тепло ингредиентам.
• Конвенция, излучение и теплопроводность — три способа передачи тепловой энергии.
• Будучи формой энергии, единицей тепла в системе СИ являются джоули.
• Кроме того, когда вещества, находящиеся в физическом контакте, не обмениваются тепловой энергией, это называется тепловым равновесием.

 

ЧТО ТАКОЕ ТЕМПЕРАТУРА?

• По сравнению с двумя вышеуказанными терминами температура — это совсем другое дело.
• Теплота или холодность объекта измеряется в данный момент времени и называется температурой.
• Определение температуры гласит, что это мера средней кинетической энергии частиц, составляющих вещество.
• Температура сама по себе ничего не может сделать; это внутреннее свойство и просто температура предмета в данный момент.
• Когда вы посещаете своего врача для осмотра, ваш врач может измерить вашу температуру, чтобы проверить наличие скачков температуры.

Источник

ОБЗОР

• Тепловая энергия – это энергия, содержащаяся в системе.
• Тепло – это поток тепловой энергии.
• Температура – ​​это средняя кинетическая энергия молекул.

Часто задаваемые вопросы

В. В чем разница между температурой, тепловой энергией и теплом?

Сравните температуру, тепловую энергию и тепло.

В. Какое состояние вещества имеет самую высокую температуру?

Газообразное состояние вещества имеет самую высокую температуру.

В. Какая самая низкая возможная температура?

Абсолютный ноль или ноль градусов по Кельвину — это самая низкая возможная температура.

В. Какова формула тепловой энергии?

Формула тепловой энергии: Q= m.c.ΔT.

Надеемся, вам понравился этот урок, и вы узнали что-то интересное о Тепло, температура и тепловая энергия! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими учениками, такими же, как и вы! Не забудьте загрузить наше приложение, чтобы испытать наши веселые классы виртуальной реальности – мы обещаем, это делает учебу намного веселее! 😎  

СПРАВОЧНАЯ ИНФОРМАЦИЯ

1. Тепло, температура и тепловая энергия: https://www.ck12.org/physics/heat-temperature-and-thermal-energy-transfer/lesson/Heat-Temperature-and-Thermal- Energy-Transfer-PHYS/#:~:text=Сводка,%20%20самая низкая%20возможная%20температура. По состоянию на 11 апреля 2022 г.
2. Heat: https://en.wikipedia.org/wiki/Heat. Доступ 11 апреля 2022 г.

Формула тепловой энергии — GeeksforGeeks

Тепловая энергия — это энергия, существующая в системе. Он отвечает за поддержание температуры системы. Тепло – это передача тепловой энергии. Термодинамика — это дисциплина физики, изучающая перенос тепла между различными типами систем. Это также касается способа выполнения задачи на протяжении всей процедуры.

Тепловая энергия

Энергия, полученная из тепла, называется тепловой энергией. Движение мелких частиц внутри системы обычно вызывает выделение тепла за счет тепловой энергии. Это энергия, которая позволяет теплу циркулировать внутри системы. В большинстве случаев тепло генерируется при движении частиц внутри объекта.

Тепловая энергия отвечает за температуру системы и является компонентом общей энергии системы, состоящей из потенциальной и кинетической энергии. Q — общепринятый способ выражения тепловой энергии. Его масса, разность температур и удельная теплоемкость прямо пропорциональны.

Тепловая энергия измеряется в Дж , единице измерения СИ (Дж).

Формула тепловой энергии

Формула для тепловой энергии заключается в следующем:

Q = MCΔT

, где

• Q = термическая энергия
• M = Give Supt Supt Svief
• 3333333333333333333. тепло
• ΔT = разница температур

Вывод формулы

Имеем,

Удельная теплоемкость = (Подводимая тепловая энергия) / ((масса) × (Изменение температуры))

Однако, поскольку формула требует специальных символов, мы можем сказать, что C означает удельную теплоемкость, T обозначает температуру, а Et обозначает тепловую энергию. Однако важно понимать, что T не используется как отдельная фраза; скорее, он представляет собой изменение T во времени. ΔT — наиболее распространенный символ изменения — Δ. При этом можно предположить, что входом является величина, определяющая изменение тепловой энергии, которое обозначается ΔEt.

Таким образом, c = (ΔE _t )/(m × ΔT)

∴ ΔEt = mcΔT

Задачи образца

6 Вопрос 1. Задан образец

6 . составляет 0,068 Дж/кг °С. Разница температур указана как 23°C. По полученным данным определить тепловую энергию вещества.

Ответ:  

Дано: m = 16 кг, c = 0,068 Дж/кг °C, ΔT = 23 °C.

Так как,

Q = mcΔT

∴ Q = 16 × 0,068 × 23

∴ Q = 25,02 Дж

Вопрос 2. Предположим, что вещество массой 12 кг изменяет температуру на 55 градусов Цельсия/кг при удельной теплоемкости 0,04 °C. . По полученным данным определите тепловую энергию соединений.

Ответ:

Дано: m = 12 кг, c = 0,04 Дж/кг °C, ΔT = 55 °C.

Поскольку,

Q = mcΔT

∴ Q = 12 × 0,04 × 55

∴ Q = 26,4 Дж

Вопрос 3. Когда вы сообщаете энергию 1800 Дж, насколько повысится температура 263 г воды? Вода имеет удельную теплоемкость 3482 Дж/кг°C.

Ответ:

Дано: m = 263 g = 0,263 кг, C = 3482 J/кг ° C, Q = 1800 Joules

с

Q = MCΔT

ΔT = Q/MC,

Q = MCΔT

ΔT = Q/MC,

.

∴ ΔT = (1800) / (0,263 × 3482)

∴ ΔT = 1800 / 915,8

∴ ΔТ = 1,965 °С.

Вопрос 4. Если удельная теплоемкость меди 453 Дж/кг°С, сколько энергии потребуется, чтобы поднять температуру 0,36 кг меди на 23°С?

Ответ:

Дано: m = 0,36 кг, c = 453 Дж/кг °C, ΔT = 23 °C.

С тех пор,

Q = MCΔT

∴ Q = 0,36 × 453 × 23

∴ Q = 3750,8 Joules

Вопрос 5. Масса вещества составляет 20 кг, а ее термическая энергия – 686. J. Разница температур составляет 23°C. На основании фактов определите удельную теплоемкость.

Ответ:

Дано: M = 20 кг, Q = 686 J, ΔT = 23 ° C

С

Q = MCΔT

∴ C = Q/MΔ

∴ C = (

∴ C = Q/MδT

∴ C = ( 686) / (20 × 23)

∴ c = 686 / 460

∴ c = 1,491 Дж/кг °C

Вопрос 6. Определите, до какой степени повысится температура 23 кг воды после передачи около 1900 Дж энергии, используя удельную теплоемкость воды 3820 Дж/кг °C.

Ответ:

Дано: M = 23 кг, C = 3820 J/кг ° C, Q = 1900 Joules

,

Q = MCΔT

δ ΔT = Q/MC

ΔT = (1900) / (23 × 3820)

∴ ΔT = 1900 / 8786

∴ ΔT = 0,2162 °С.

Вопрос 7. Что такое единица СИ для тепловой энергии?

Ответ:

Единицей тепловой энергии в системе СИ является Джоуль.